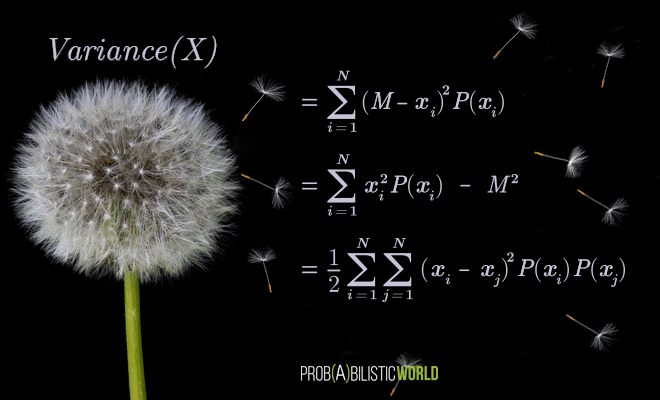
In today’s post I want to show you two alternative variance formulas to the main formula you’re used to seeing (both on this website and in other introductory texts).
Not only do these alternative formulas come in handy for the derivation of certain proofs and identities involving variance, they also further enrich our intuitive understanding of variance as a measure of dispersion for a finite population or a probability distribution.
[Read more…]
A few posts ago I introduced you to the “three M’s” of statistics — the concepts of mean, mode, and median. Today I want to talk to you about a related concept called variance.
While the three M’s measure the central tendency of a collection of numbers, the variance measures their dispersion. That is, it measures how different the numbers are from each other.
Measuring dispersion is another fundamental topic in statistics and probability theory. On the one hand, it tells you how much you can trust the central tendency measures as good representatives of the collection. High variance usually means a lot of the numbers in the collection will be far away from those measures.
Expected value is another central concept in probability theory. It is a measure of the “long-term average” of a random variable (random process). I know this doesn’t sound too clear, but in this post I’m going to explain exactly what it means.
There are many areas in which expected value is applied and it’s difficult to give a comprehensive list. It is used in a variety of calculations by natural scientists, data scientists, statisticians, investors, economists, financial institutions, and professional gamblers, to name just a few.
The concepts of mean, median, and mode are fundamental to statistics, probability theory, and anything related to data analysis as a whole. Being this important, they deserve their own introduction.
In statistics, these 3 concepts are examples of measures of central tendency. This is a fancy way of saying that they are single values that summarize collections of values.
Let’s unpack the last sentence. What exactly do I mean by ‘values’ and ‘collections of values’?
Throughout history, we have come up with better and more accurate ways to measure physical quantities like time, length, mass, and temperature. This has been crucial for our scientific and technological development.
Each of these quantities has a precise definition and is informative about some aspect of the current state of the physical world. For example, the mass of an object can tell you how much work is necessary to lift it at a certain height. The outside air temperature determines the kind of clothes you would wear when you go out. And so on.
Probabilities are also quantities that measure something — they have a very precise and unambiguous mathematical definition. But still, they don’t relate to things in the physical world as straightforwardly and as intuitively as measures like mass and length.
If you ever took an introductory course in statistics or attempted to read a publication in a scientific journal, you know what p-values are. Оr at least you’ve seen them. Most of the time they appear in the “results” section of a paper, attached to claims that need verification. For example:
The stuff in the square brackets is usually other relevant statistics, such as the mean difference between experimental groups. If the p-value is below a certain threshold, the result is labeled “statistically significant” and otherwise it’s labeled “not significant”. But what does that mean? What is the result significant for? And for whom? What does all of that say about the credibility of the claim preceded by the p-value?
There are common misinterpretations of p-values and the related concept of “statistical significance”. In this post, I’m going to properly define both concepts and show the intuition behind their correct interpretation.
If you don’t have much experience with probabilities, I suggest you take a look at the introductory sections of my post about Bayes’ theorem, where I also introduce some basic probability theory concepts and notation.