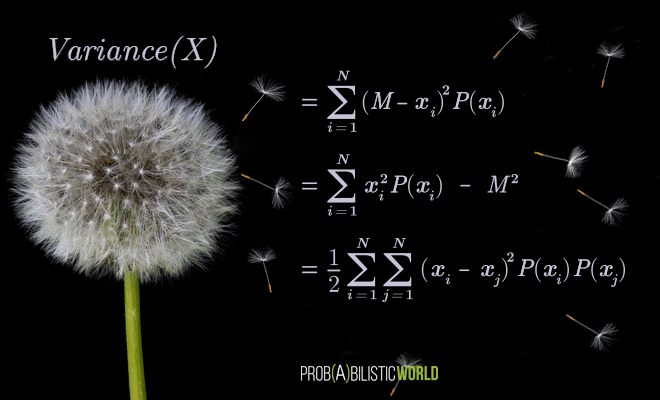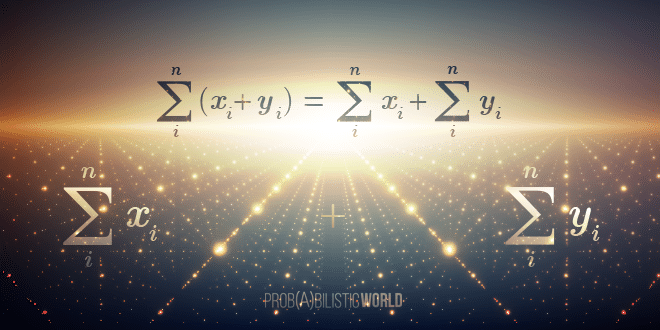Probabilistic World

Introduction to Number Theory: The Basic Concepts

Posted on Written by 1 Comment

Portrait of Pierre de Fermat and Marin Mersenne

Hi, everyone. Today I want to talk about number theory, one of the most important and fundamental fields in all of mathematics. This is a field that grew out of arithmetic (as a sort of generalization) and its main focus is the study of properties of whole numbers, also known as integers.

Concepts and results from this field are important enough to have implications for (and be used in) almost every branch of mathematics. And not just mathematics. Number theory is also extremely fundamental to fields like cryptography and computer science and has applications in many other sciences, like physics and chemistry.

[Read more…]

Euclidean Division: Integer Division with Remainders

Posted on Written by 2 Comments

Four servings of vanilla ice cream on a black background, with a spoon of one serving below as "remainder"

In today’s post I want to talk about Euclidean division. This is a more general definition of division between two integers because, unlike regular division, it’s defined for any pair of integers (except when the divisor is 0). I originally wanted to cover this topic in my post on negative numbers. But I decided to take it out in a separate post in order to keep the length below some reasonable limit.

[Read more…]

Negative Numbers and Arithmetic: Intuition

Posted on Written by Leave a Comment

Many numbers of different sizes with the planet Earth in the background and the text "negative numbers" in the foreground

Hi everyone, and welcome to the next post from our journey in the world of numbers. Where we last left off, I was telling you about natural numbers — the objects that most naturally appear when we make our first steps in the world of Mathematics. Well, today’s post is about the next most natural kind of mathematical objects: negative numbers and the new structure they form together with natural numbers called integers!

This post is part of my series Numbers, Arithmetic, and the Physical World.

[Read more…]

Alternative Variance Formulas and Their Derivation

Posted on Written by 2 Comments

The equations of three alternative variance formulas

In today’s post I want to show you two alternative variance formulas to the main formula you’re used to seeing (both on this website and in other introductory texts).

Not only do these alternative formulas come in handy for the derivation of certain proofs and identities involving variance, they also further enrich our intuitive understanding of variance as a measure of dispersion for a finite population or a probability distribution.

[Read more…]

The Sum Operator: Everything You Need to Know

Posted on Written by 1 Comment

The sum operator (capital Greek letter Sigma), light beams in the background

I have used the sum operator in many of my previous posts and I’m going to use it even more in the future. I’ve introduced bits and pieces about this notation and some of its properties but this information is scattered across many posts. For these reasons, I decided to dedicate a special post to the sum operator where I show you the most important details about it.

[Read more…]

Natural Numbers and Arithmetic: Intuition

Posted on Written by 1 Comment

Many numbers of different sizes with the planet Earth in the background and the text "natural numbers" in the foreground

Welcome to the third post from my series on numbers and arithmetic. In the previous two posts, I gave an overview of real numbers (and their main subsets), as well as the main operations between them. And in the rest of the series, we’re going to build all these concepts from scratch. Well, the focus in today’s post is the most basic subset of the real numbers: the natural numbers.

This post is part of my series Numbers, Arithmetic, and the Physical World.

[Read more…]