
Expected value is another central concept in probability theory. It is a measure of the “long-term average” of a random variable (random process). I know this doesn’t sound too clear, but in this post I’m going to explain exactly what it means.
There are many areas in which expected value is applied and it’s difficult to give a comprehensive list. It is used in a variety of calculations by natural scientists, data scientists, statisticians, investors, economists, financial institutions, and professional gamblers, to name just a few.
Expected value is closely related to the concept of arithmetic mean I talked about in the post dedicated to the 3 main measures of central tendency. From another perspective, it’s also closely related to the law of large numbers which I introduced in my last post. If you’re not familiar with these concepts, I recommend reading the 2 posts for an intuitive introduction. But even if you are familiar, the posts will likely give you a different perspective and still enrich your understanding of these concepts. I also plan to use some of the intuition from the posts in explaining expected value itself. All in all, consider these two posts recommended readings.
Also, check out my post on the mean and variance of probability distributions for even more intuition on this topic. In particular, to see why the mean and the expected value of a random variable are the same thing.
And with that out of the way, let’s see what expected value is all about.
Table of Contents
Introduction
Let’s say you work for a company that pays you a fixed salary of $7500 every month. In terms of daily expenses, you spend exactly $2500 in total every month and you put the rest in your personal bank account. Also, say you start with exactly $0 in your account on the 1st of January. How much money do you expect to have by the 1st of January the following year (12 months later)?
That’s easy. You put $7500 – $2500 = $5000 in your account every month. So, after 12 months you get $5000 * 12 = $60000.

To simplify things, let’s assume the following bonus probabilities every month (each month’s bonus is independent of the rest):
- $1000 with probability 0.6
- $500 with probability 0.3
- $0 with probability 0.1
Now let’s ask the same question again: how much do you expect to have in your account after 12 months of work?
You know you’re getting $60 thousand from the fixed salary for sure (after subtracting your monthly expenses). On top of that, you’ll add an uncertain amount from the bonuses. But how much?
The obvious answer is that you don’t know for sure. And it’s true, you can’t know the exact amount with complete certainty.
For example, it’s not impossible that you get very unlucky and receive $0 in bonuses for all 12 months. In such a case, in the end you’ll still have only $60 thousand. Because the bonus probabilities are independent, the probability of getting no bonus every month is 0.1 multiplied 12 times: 0.112 = 0.000000000001 (take a look at my post on compound event probabilities if you’re unsure about why this is so). Very unlucky indeed! But you probably know better than to worry too much about such small probabilities.
On the other hand, you can also get very lucky and get the maximum bonus of $1000 every month, for a total of $12 thousand by the end of the year. The probability of this event is 0.612 ≈ 0.002. This isn’t as small as the previous case but it’s still not very impressive.
So, what amount do you expect to have in your account by the end of the year after all? We already know the lower bound to the answer is $60 thousand and the upper bound is $72 thousand. But we saw that both of these extremes have tiny probabilities, so most likely the actual amount will be somewhere between them. But is there a value within the range 60000-72000 that’s somehow more special than the others? One that you should expect more than the rest?
Yes, there is. And it’s called… the expected value.
Expected value
In this section, I’m going to show you the formal definition of expected value and how to actually calculate it. I’m also going to give you some intuition about it by showing its relationship to the arithmetic mean and the law of large numbers. As always, I’m going to give you a few examples to help everything sink in.
In fact, let’s start with our very first example and finally answer the question from the end of the previous section. I’m going to show you how to calculate the expected value in this particular example without too much explanation and I’ll give the details afterwards.
First, let’s calculate the expected bonus per month. You do this by multiplying each possible value by its respective probability and add the products.
Remember, the bonus probabilities were:
- $1000 with probability 0.6
- $500 with probability 0.3
- $0 with probability 0.1
Therefore, the expected value for 1 month is:
Then, you multiply this by 12 to get the expected bonus amount for 12 months:
So, by the end of the year, the expected value of your bonuses is $9 thousand. There’s our answer!
Of course, you add the bonuses to your fixed income to get a final expected value of $69 thousand.
See, it wasn’t hard at all. Now let’s get some deeper understanding about the calculation I just made.
Formal definition of expected value
First, let’s define the distinction between deterministic and random variables.
A deterministic variable is a variable with only one possible fixed value at any given time. For example, your current age is a deterministic variable. To find its value, all you need to do is subtract your birth date from the current date (and optionally convert from days to years). No matter how many times you perform this measurement, you will always get the same result. In other words, your age is a fixed value (at any particular moment in time).

Now let’s consider the general case. Let’s say that any random variable can have N number of possible values: v1, v2, v3, …, vN (N can be any number greater than 1). Let’s also denote the probabilities of the values as P(v1), P(v2), P(v3), …, P(vN).
As you might remember from the discussion in my sample space post, the probabilities of all possible values must add up to 1. That is, P(v1) + P(v2) + P(v3) + … + P(vN) = 1.
With these notations in mind, the expected value (EV) of a random variable for a single observation is given by the following expression:
Do you see how we applied this general formula to the salary-bonus example above? Take some time to make sure you understand the correspondence between the terms and the specific values from the example.
Well, now you have the formal definition of expected value. In the next sections, I’m going to give you some intuition about what exactly it measures and clear up some potential confusions.
Before I do that, I want to quickly introduce a mathematical notation that allows you to write the above expression in a more compact way.
The sum operator
To learn more about the sum operator, check out my post dedicated on this notation and its properties.
The sum operator Σ is a convenient mathematical notation for expressing the sum of a set or a sequence of values. The mathematical symbol used for the sum operator is the Greek capital letter Sigma. Take a look:
On the left-hand side of the equation, N number of values are being added up. The values are expressed as the variable x with a numerical subscript. The subscript indicates the index of the element in the sequence.
On the right-hand side, we have the same sum expressed with the sum operator. It consists of 4 parts:
- The Σ symbol, indicating a sum operation
- The n=1, indicating that the index starts from 1
- N, indicating that the index goes up to N
- xn, which is the actual addition term
The index is incremented by 1 on each iteration (for each term of the sum). Instead of xn, you can have an arbitrarily complex expression that consists of terms (optionally) indexed by n. Here’s how you can write the expected value of a random variable with N possible values:
To expand this, you just need to substitute the n index with the concrete numbers as you go from 1 to N. For example, for a random variable with 3 possible values, expanding the expression above would look like this:
Notation
Before I give you a few examples, I want to show you a common convention for a short-hand expected value notation. If you have a random variable X with N possible values , then we express the expected value of X with the capital letter E in blackboard bold:
Or simply or
. Less commonly, you may even see it expressed as:
You may also hear the term “the expectation of X” which is a short way of saying “the expected value of the random variable X”.
Anyway, I’m showing you these different notations here just so you’re familiar with them and you’re not surprised if you come across them in other texts (including my posts). For the rest of this post, let’s stick with the EV(X) notation.
Examples and simulations
I want to convince you that the expected value is indeed a number that should be “expected”. Let’s confirm this with a few experimental simulations.
First, let’s look at the bonus-salary example we started with. Remember we calculated the bonus expected value for 1 month to be $750. Let’s see if that’s really the case.
In the animated plot below, you’ll see the running average of the bonuses after up to 50 months of working for the company. A running average is simply the average calculated after every month by dividing the sum of all bonuses by the number of months passed since month 0.
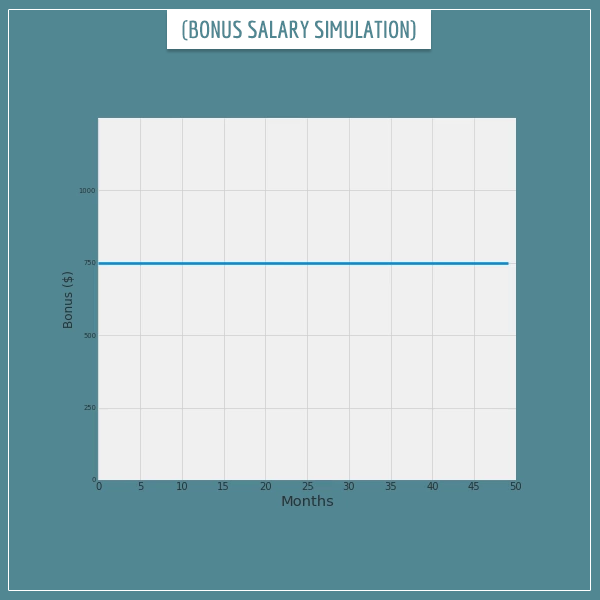
The blue line indicates the expected $750 monthly bonus. Do you see how, as the number of months increases, the average monthly bonus starts converging towards the expected value? Those of you who read my post on the law of large numbers will find this example very familiar.
Let’s run the same simulation even longer. What happens to the monthly average after working for the company for 10 years?
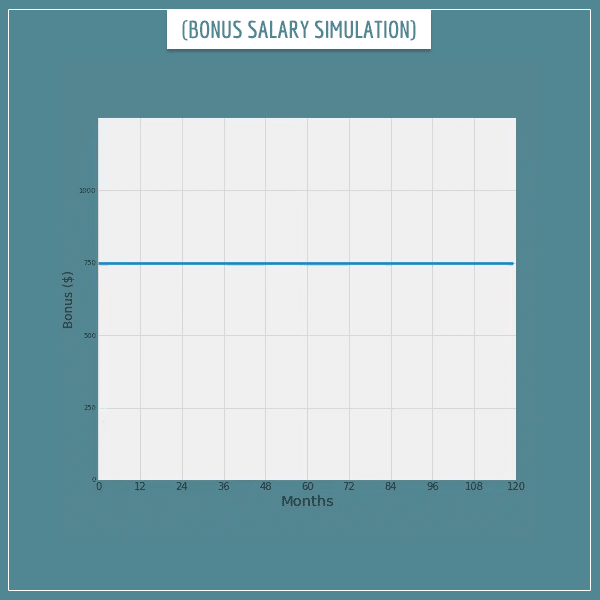
With increasing number of months, notice how the real running average deviates less and less from the expected value!
Alright, let’s look at something different. I’m going back to my favorite coin flip example.
Say someone offers you to play a game. A coin will be flipped and if it comes up heads, you win $2. If it comes up tails, you need to pay $1. Would you play the game?
Not playing the game guarantees $0 win and $0 loss. So, the way to make a choice would be by calculating the expected value of the flip and only play the game if it’s greater than $0. Let’s see:
Notice how one of the possible values is negative this time. A good opportunity to see this doesn’t change the expected value calculations at all.
So, since the expected value is $0.5, the game should be profitable to play. If you had the option to play it multiple times, you should take that too. In fact, how much money do you expect to have won after playing the game, say, 1000 times? The answer is $0.5*1000 = $500.
Let’s see this in action. The following 3 animated plots show the results of flipping 1 fair coin 1000 times. The first plot shows the % of heads after each flip. The next plot shows the corresponding average money won per flip. Finally, the third plot shows the total money won after each flip.
Take a look:
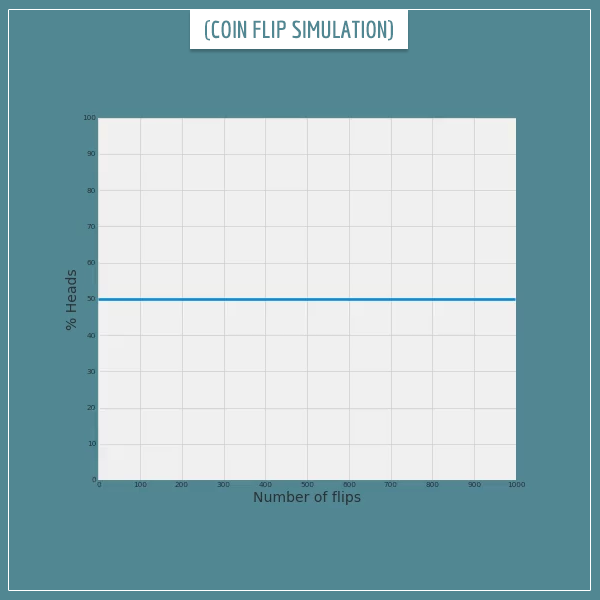
Here’s the average winnings per flip:
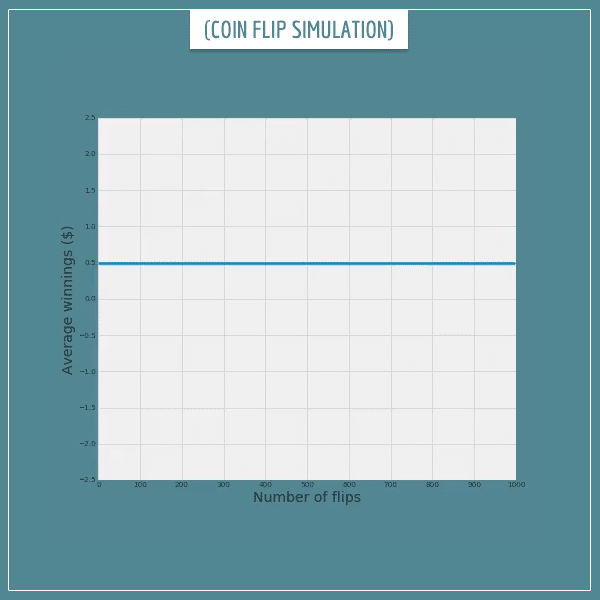
And here’s the total winnings after each flip:
All plots show exactly what we expected! The long-term average of the winnings does converge to the expected value and the total winnings get very close to the expected $500.
Of course, the actual trajectory is different every time. The empirical long-term average does fluctuate around the expected value which makes the total winnings swing up and down. But those fluctuations are local and, in the long-run, observations deviate less and less from the expectations.
In short, if someone offered you this game for 1000 flips, you can safely rely on winning some amount very close to $500.
Expected value intuition
So, why does all this work? We know individual outcomes are independent of each other and have no memory of previous outcomes. How do the values of the outcomes always manage to arrange themselves so that their long-term average keeps getting closer to the expected value?
The key to answering this question is in the relationship between expected value, arithmetic mean, and the law of large numbers.
Imagine you had a finite sequence of 1000 coin flips whose outcomes you already know. Let’s say they somehow happened to be exactly 500 heads and 500 tails. If you were playing the game from the previous section, you would immediately know how much you would win even before the game. For every heads you get $2, so $2 * 500 = $1000. For every tails you give $1 which is $1 * 500 = $500. Therefore, your bottom line from the game would be $1000 – $500 = $500.
Notice that this will be true even if you change the number of coins from 1000 to something else. As long as exactly half of the coins are heads, your final winnings will be equal to $0.5 times the number of flips.
Now imagine an infinite sequence of coin flips. Perhaps a robot has been programmed to flip a coin, pick it up, and flip it again, forever. From the law of large numbers we know that, as the number of flips increases, the heads % will get closer and closer to 50%.
Say you take a snapshot of this infinite sequence after N number of flips. If the % of heads in this sub-sequence is close to 50%, then your winnings will be very close to $0.5 * N. So, all you need to do is take a large enough N to make sure that the % of heads is really close to 50%. The law of large numbers guarantees this will work.
Another way to look at this is that, as N increases, the sequence becomes more and more like you replaced every single outcome with the long-term average (mean) of the sequence.
The same would be true in the general case where you have a random variable with more than 2 possible values. Because of the law of large numbers, you can count on the fact that the relative frequency (percentage) of each value will approach its probability.
For a discussion on the rate of convergence, check out the How large is large enough? section of my post on the law of large numbers.
Discrete versus continuous random variables
Throughout this post I’ve been assuming we’re working with discrete random variables. With continuous random variables, the sum operator is replaced by an integral. For more details on this, check out my posts on probability distributions and the mean and variance of probability distributions.
Integrals are a somewhat more complicated mathematical concept and I don’t want to make this lengthy post even lengthier. However, the idea and intuition of expected value for the continuous case is almost the same as for the discrete case. If you’re still curious about integrals and discrete vs. continuous random variables, you can read my post on zero probabilities (particularly the Integrals section). And, of course, feel free to ask any questions beyond what I covered in this or that post in the comment section below.
Summary
The expected value of a random variable is the long-term average of its possible values when values have been realized a large number of times. It is equal to the sum of the products of the values and their probabilities.
Like the law of large numbers, the expected value of a random variable is a bridge between theoretical expectations and empirical observations. The two are so closely connected that the main formulations and proofs of the law of large numbers are centered around the expected value of an arbitrary random variable.
Having a good understanding of expected value is crucial for anybody who wants to delve deeper into probability theory, statistics, and all of their related fields. You will further see how important it is in some of my future posts where I’ll discuss other theoretical concepts like probability distributions, as well as some practical application of probability theory.
I hope you found this post useful. Please share your thoughts and questions in the comment section below!

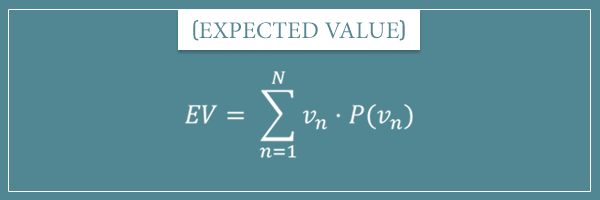
![Rendered by QuickLaTeX.com \[\mathop{\mathbb{E}[X] = \sum_{n=1}^{N} x_n \cdot P(x_n)\]](https://www.probabilisticworld.com/wp-content/ql-cache/quicklatex.com-d5934bfe669abb717715811dd515f72c_l3.png)
Great Article. I don’t think there could be a more intuitive explanation. Thanks.
Thank you for your explanations, they are very clear and interesting.
great article. really helped me understand expected value. btw do you suggest any video lecture series or books to study probability and statistics and have an intuitive understanding of them?
Hi, Jon, I’m glad you found this post helpful!
Most books on probability theory I’ve come across (even the ones which are for “beginners”) still require a good background in mathematics (and possibly programming). Trying to fill this gap is part of my motivation for trying to write the posts the way I do. I try to explain probability theory related concepts more intuitively than I myself have had to study them.
However, I would recommend the probability theory related videos on Khan Academy. They aim to be as intuitive and beginner-friendly as possible.
Thanks sir, this article has certainly helped me understand quantum mechanics a lot better.
Great teaching tips. Your very simple and easy to follow examples have helped me a great deal in understanding the concepts. Thanks so much and God bless you.
I love your articles. Learned a lot of things that are so obviously useful and yet aren’t taught in school.
Thanks a lot to put it in such a simple way. It was very useful.
Thank you all, I appreciate all the positive feedback!
Just binged most of your articles. You have a talent for breaking down these things in an intuitive manner. Thank you very much for these great lessons!
Something not right with the final simulation “… and the total winnings get very close to the expected $500….” ?
I ran it a few times, and it ends up at $470 every time…
Hi Patrick, the simulations here are not run every time you click on the image. This is a single run of the simulation that I animated just for illustration. So, you are seeing the same number because you are watching the same simulation on replay 🙂
Do you have any background in programming? Would you like some help for you to code the simulation yourself?
Aha, that explains some of this…
Yes I do, would be interested to run this myself, thank you. Is the project on github?
It’s not on Github, but it’s really a few lines of code. All you need to do is generate a random array of 0s and 1s, representing the “heads” and “tails” outcomes. Then you can associate each element of the array with some number representing the payouts of the respective outcome. The sum of the second array is your cumulative winnings, whereas the average is the expected value per trial.
I encourage you to try to code it yourself, it will be a very useful and informative exercise for you! Which programming languages are you familiar with?
Hi,
The experiments taken here, for the value of Random Variable, say X, are numerical and are comparable like 100$ > 200$, obviously
But what if they are not comparable.
Say you are rolling a dice and X = the number on the face of the dice after the roll. Since all faces have equal probability of 1/6. Expected value will be 3.5.
Hi Mavy, if I understand your question correctly, you’re asking about random variables whose values are nominal (categorical) and not numerical. For example, if the die doesn’t have the numbers 1 through 6 but has different colored sides instead (red, green, etc.) what is the expected value of a single die roll? Is it supposed to be some color that is the (weighted) average of the color of each side? What does that even mean?
Well, the short answer is that expected value, as I presented it in this post, can only be calculated for random variables that take numerical values. You ask an important question, however. As it happens, in the next few weeks I’m going to publish a post I’m currently working on that specifically focuses on the questions of mean and variance of categorical probability distributions. In that post, I’m going to address your question and other related topics in more depth.
Let me know if I properly understood what you meant by ‘comparable’ and your question in general.
Hi,
Yes, this is precise thing that has been bugging me.
Thanks for understanding,
Waiting for your next post!
If head is 1 and tail is 3 expect 2 be the average of n outcome?
If you associate numerical values to the outcomes (and they are 1 and 3 like you suggest), then indeed the expected value per repetition is going to be 2.
Greatly valuable article on the expected value of a random variable. Can you shed some light on the linear combinations of random variables too?