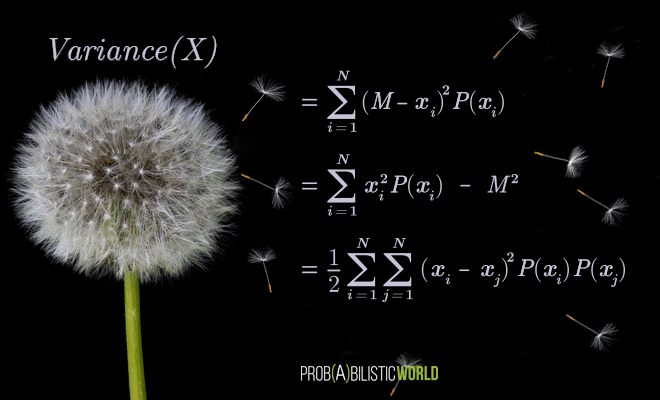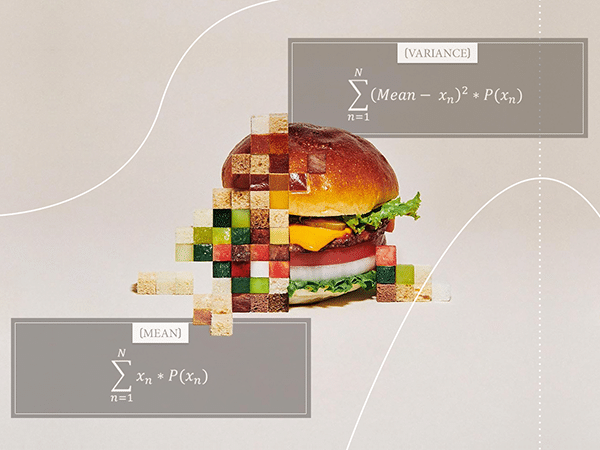In today’s (relatively) short post, I want to show you the formal proofs for the mean and variance of discrete uniform distributions. I already talked about this distribution in my introductory post for the series on discrete probability distributions. Well, this is a pretty simple type of distribution that doesn’t really need its own post, so I decided to make a post that specifically focuses on these proofs. More than anything, this is going to be a small exercise in algebra.
This post is part of my series on discrete probability distributions.
[Read more…]