Probabilistic World

Mean and Variance of Probability Distributions

Posted on Written by 13 Comments

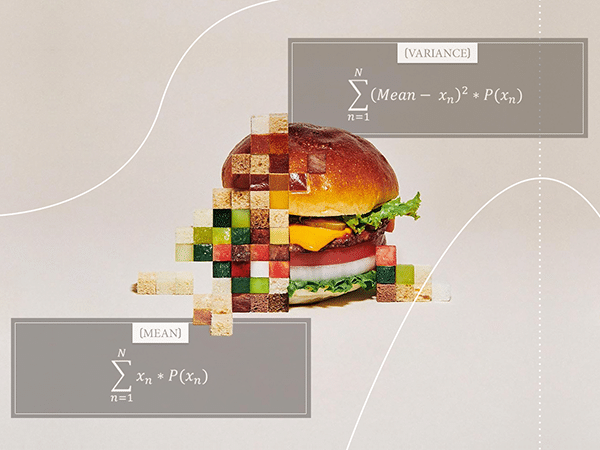
In my previous post I introduced you to probability distributions.

In short, a probability distribution is simply taking the whole probability mass of a random variable and distributing it across its possible outcomes. Since every random variable has a total probability mass equal to 1, this just means splitting the number 1 into parts and assigning each part to some element of the variable’s sample space (informally speaking).

In this post I want to dig a little deeper into probability distributions and explore some of their properties. Namely, I want to talk about the measures of central tendency (the mean) and dispersion (the variance) of a probability distribution.

[Read more…]

Introduction to Probability Distributions

Posted on Written by 7 Comments

If you want to take your understanding of probabilities to the next level, it’s crucial to be familiar with the concept of a probability distribution.

In short, a probability distribution is an assignment of probabilities or probability densities to all possible outcomes of a random variable.

For example, take the random process of flipping a regular coin. The outcome of each flip is a random variable with a probability distribution:

  • P(“Heads”) = 0.5
  • P(“Tails”) = 0.5

Depending on the type of random variable you’re working with, there are two general types of probability distributions: discrete and continuous. In this post, I’m going to give an overview of both kinds. And in follow-up posts I’m going to individually introduce specific frequently used probability distributions from each kind.

[Read more…]

The Variance: Measuring Dispersion

Posted on Written by 2 Comments

Small pawn-shaped magnets of different color, representing varianceA few posts ago I introduced you to the “three M’s” of statistics — the concepts of mean, mode, and median. Today I want to talk to you about a related concept called variance.

While the three M’s measure the central tendency of a collection of numbers, the variance measures their dispersion. That is, it measures how different the numbers are from each other.

Measuring dispersion is another fundamental topic in statistics and probability theory. On the one hand, it tells you how much you can trust the central tendency measures as good representatives of the collection. High variance usually means a lot of the numbers in the collection will be far away from those measures.

[Read more…]

Intuitive Explanation of Expected Value

Posted on Written by 20 Comments

A pile of poker chips and a few dice

Expected value is another central concept in probability theory. It is a measure of the “long-term average” of a random variable (random process). I know this doesn’t sound too clear, but in this post I’m going to explain exactly what it means.

There are many areas in which expected value is applied and it’s difficult to give a comprehensive list. It is used in a variety of calculations by natural scientists, data scientists, statisticians, investors, economists, financial institutions, and professional gamblers, to name just a few.

[Read more…]

The Law of Large Numbers: Intuitive Introduction

Posted on Written by 17 Comments

The silhouette of an infinity symbol
The law of large numbers is one of the most important theorems in probability theory.  It states that, as a probabilistic process is repeated a large number of times, the relative frequencies of its possible outcomes will get closer and closer to their respective probabilities.

For example, flipping a regular coin many times results in approximately 50% heads and 50% tails frequency, since the probabilities of those outcomes are both 0.5.

The law of large numbers demonstrates and proves the fundamental relationship between the concepts of probability and frequency. In a way, it provides the bridge between probability theory and the real world.

[Read more…]

The Mean, the Mode, And the Median

Posted on Written by 3 Comments

Mean, median, and mode of a distribution shown on a Spaghetti Western background

The concepts of mean, median, and mode are fundamental to statistics, probability theory, and anything related to data analysis as a whole. Being this important, they deserve their own introduction.

In statistics, these 3 concepts are examples of measures of central tendency. This is a fancy way of saying that they are single values that summarize collections of values.

Let’s unpack the last sentence. What exactly do I mean by ‘values’ and ‘collections of values’?

[Read more…]