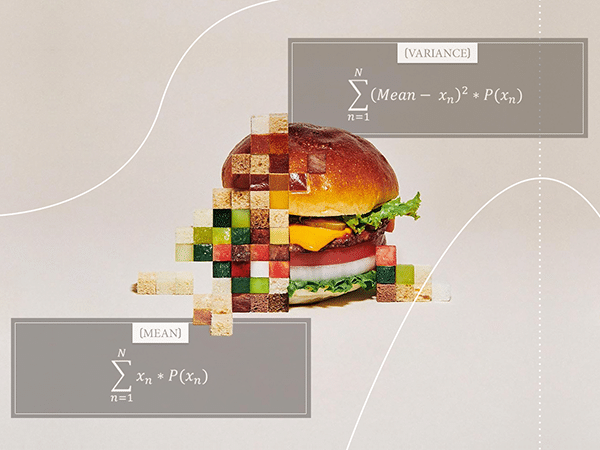This is a bonus post for my main post on the binomial distribution. Here I want to give a formal proof for the binomial distribution mean and variance formulas I previously showed you.
This post is part of my series on discrete probability distributions.
[Read more…]