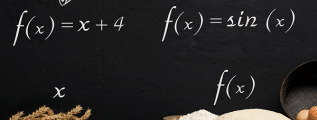
The topic of today's post is mathematical functions. Functions are such a fundamental part of mathematics that you're certain to encounter them almost everywhere. Recently, I started a small series on numbers and arithmetic, in order to begin … [Continue reading]




