
Welcome to the second post from my series on numbers and arithmetic. As a sort of continuation to the introductory post, here I want to talk about the most important properties of arithmetic operations.
This post is part of my series Numbers, Arithmetic, and the Physical World.
In the introductory post, I told you about the fundamental arithmetic operations addition, multiplication, and exponentiation, as well as their inverses subtraction, division, roots, and logarithms. All of these are examples of binary operations, which means they work with exactly two numbers.
Now let’s take a look at the main properties of these arithmetic operations. In the next posts, we’re going to be building their intuition as we gradually build the full set of real numbers.
Table of Contents
General arithmetic properties
First let’s look at the main properties that apply to more than one operation. In this section I’m going to describe the properties in a general and abstract way and in the next sections I’m going to discuss which of these hold for which particular arithmetic operations.
Let’s use the symbol to represent an arbitrary arithmetic operation.
The commutative property
The commutative property is one of the most fundamental arithmetic properties. If an operation has this property, it means that for any two numbers a and b:
In other words, if you switch the two numbers so that the first becomes the second and the second becomes the first, the result of the operation remains the same.
The associative property
The associative property is another very fundamental property of arithmetic operations.
Even though binary operations work with only two numbers, you can still have expressions containing more than one operation and more than two numbers. In such cases, the order in which you apply the separate operations may be important for the final result. In the previous post I talked about using parentheses or brackets to specify this order (when necessary).
With this in mind, the associative property is about expressions with more than two numbers where the same binary operation is applied. If an operation has the associative property, this means that for any three numbers a, b, and c:
That is, if you have an expression with three numbers, the order in which you apply the operation doesn’t affect the final result. Which essentially allows you to drop the parentheses in the expression.
This can naturally be extended to more complex expressions with more than three numbers:
Identity and inverse elements of an operation
If an operation has a left identity element l, this means that for every number a:
On the other hand, if an operation has a right identity element r, this means that for every number a:
Finally, if an operation has both a left and a right identity element and the two are the same number (), we simply say that the operation has an identity element e:
In words, the identity element of an operation is one which leaves all numbers unchanged when you apply the operation on them along with the identity element.
Operations can have a left or a right identity element, both, or neither. Under operations which have both (ones with an identity element), numbers have so-called inverse elements. If you apply the operation on an number and its inverse, the result is the identity element of the operation. That is, if the number b is the inverse of a:
You might be wondering if there’s a relationship between the concepts of inverse operations and inverse elements. And there actually is, although the two are still distinct notions. I’m going show examples of this in the next sections but, for now, let’s only say the following. If e is the identity element of the operation
The distributive property
All the properties we’ve looked at so far concern a single binary operation. On the other hand, the distributive property is a property of two binary operations. Say and
are two arbitrary binary operations and a, b, and c are three arbitrary numbers.
If distributes over
on the left, then:
Similarly, if
And if
By the way, notice that if is commutative and it distributes over another operation on the left, this implies that it also distributes on the right, and vice versa. And, conversely, if
isn’t commutative, it can’t distribute both on the left and on the right.
Properties specific to arithmetic operations
Alright, so far we’ve looked at these properties on a more abstract level. Now let’s see which of them hold for the main arithmetic operations.
In the subsections below we’re going to look at each operation individually and consider all of their properties – the main ones from the previous section, as well as properties which are only relevant for a particular operation.
Addition
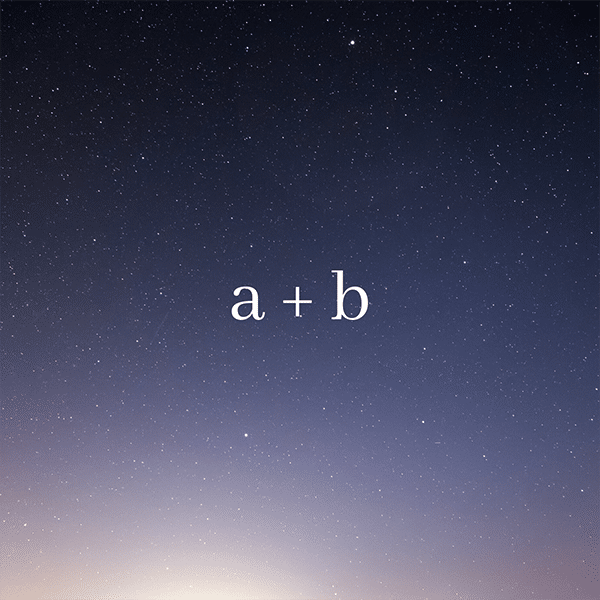
The first thing to note about addition is that this operation is valid for any two real numbers. As you’ll soon see, this isn’t true for all operations.
First, is the commutative property valid for addition? Yes it is:
For example:
Similarly, the associative property also holds for addition:
For example:
Addition has an identity element which is 0:
For example:
And all real numbers also have inverse elements under addition. A number’s inverse is simply the additive inverse of the number I mentioned in the introductory post. For example, the inverse of 2 is -2 and the inverse of -2 is 2. The number 0 is the only one which is its own inverse because
And, accordingly, when we add a number to its inverse, we get the identity element:
Subtraction
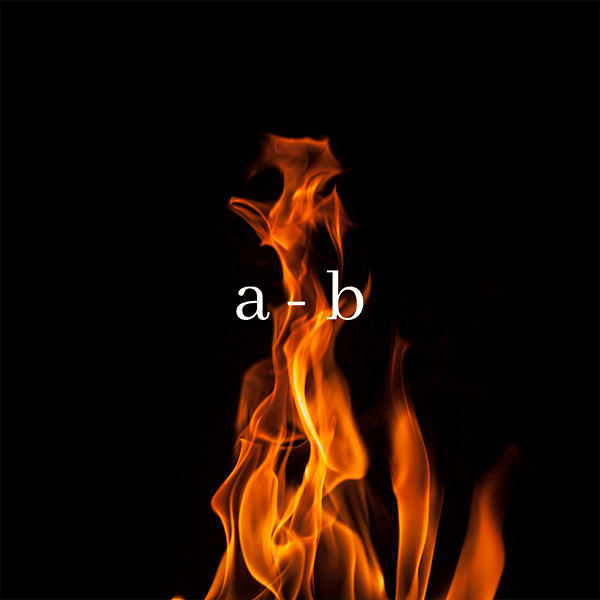
Like addition, subtraction is valid for all real numbers.
However, subtraction lacks the commutative propety because, generally:
For example:
Subtraction also lacks the associative property:
For example:
Subtraction only has a right identity element, which is also 0:
But 0 isn’t the identity element for subtraction, since:
Does the last expression remind you of something from an earlier section of this post? Remember that when you apply the inverse of an operation on the operation’s identity element and an arbitrary number, you get the inverse of that number:
Which is exactly what the
Finally, because subtraction doesn’t have an identity element, it also doesn’t have inverse elements.
Multiplication
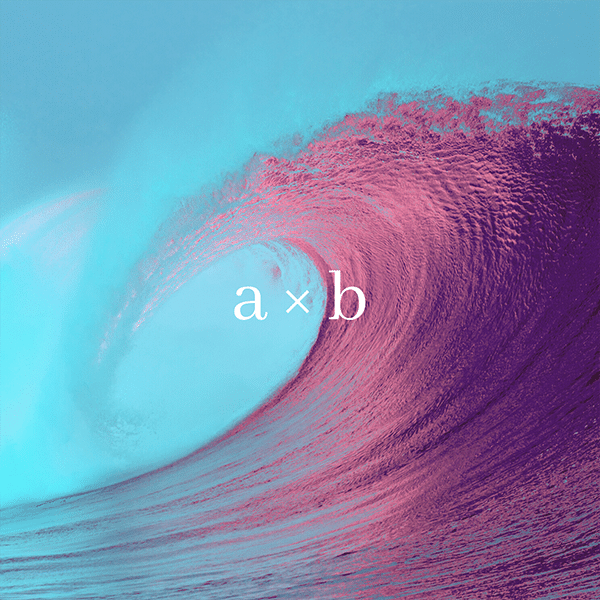
Like addition and subtraction, multiplication is valid for all real numbers. Before we look at the main properties, let’s address another important thing about multiplication. Namely, multiplication by negative numbers.
In a nutshell, multiplying:
- two positive numbers results in a positive number
- a positive and a negative number results in a negative number
- two negative numbers results in a positive number
For example:
Like addition, multiplication has both the commutative and associative properties:
For example:
The identity element for multiplication is 1 because:
For example:
Under multiplication, the inverse element of each number is its multiplicative inverse (which I also talked about in the introductory post). For example, the inverse of
And, according to the inverse element property, we have:
Division
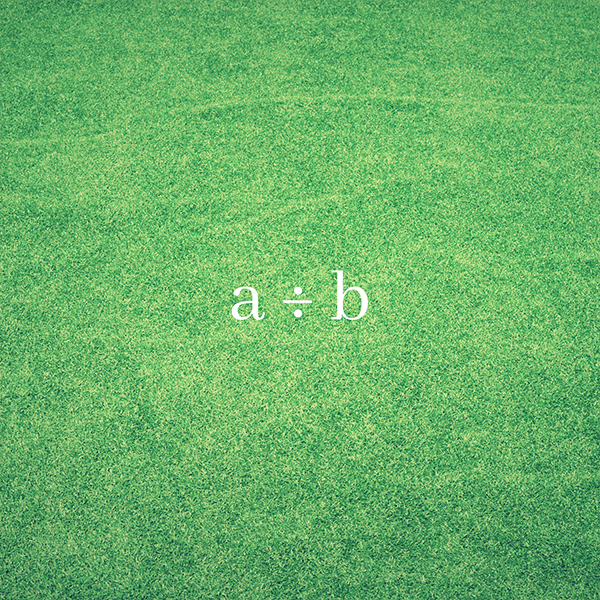
Division is valid for all real numbers, except when the second number is 0. Which is the point I left you with in the last section. I’m going to address this in more detail in the post on natural numbers bur, for now, just remember that dividing any number by 0 (including 0 itself) is not valid.
Similar to multiplication, a division operation involving a negative and a positive number results in a negative number and one involving two negative numbers results in a positive number. For example:
Like subtraction, division doesn’t have the commutative property:
For example:
And it doesn’t have the associative property:
For example:
Also, like subtraction, division only has a right identity element equal to 1:
Which isn’t an identity element because
Exponentiation

As a quick reminder on exponentiation terminology, the number being raised to a power is called the base and the power itself is called the exponent. So, for which real numbers is exponentiation valid?
Well, first, if the base is a positive real number, the exponent is allowed to be any real number (positive, negative, or zero). Second, if the base is 0, the exponent cannot be a negative number. It can be zero, although the status of is somewhat special and it’s actually a source of a small debate within the mathematical community. The most common agreement is that
but in some fields they prefer to treat it as an invalid operation. In rare cases, you might even see
. Finally, if the base is a negative number, the exponent can only be an integer or a rational number whose denominator is an odd number.
I’m going to address all these constraints (and the intuition behind them) in more detail in the next posts of this series. For now, let’s get back to the main properties.
The commutative property doesn’t hold for exponentiation:
For example:
The associative property also doesn’t hold:
For example:
Exponentiation only has a right identity element equal to 1:
But 1 isn’t an identity element because, in the general case:
And because exponentiation doesn’t have an identity element, here there are no inverse elements either.
More exponentiation properties
Here I want to talk about some exponentiation-specific properties that aren’t part of the general properties.
The first such property to notice is:
In words, raising any number to the power of -1 results in 1 divided by that number. But we already knew this because this is nothing but the unary operation called multiplicative inverse. Now you know where this notation is coming from.
And here’s another important property:
In words, raising a number to a power which is already raised to another power is equal to the number raised to the product of the powers.
And, from these two, we can derive a more general version of the first property by setting in the second property:
So, when you raise a number (a) to the additive inverse of another number (b), this results in the multiplicative inverse of
What if we raised a number to the multiplicative inverse of another number? Well, then we get the following important property:
For example,
Roots

The constraints regarding which numbers the root operation is valid for are very much related to the constraints for the exponentiation operation. For example, roots of negative numbers where the power is an even integer are undefined, since the result of raising any number to an even power is a positive number. For example, expressions like or
aren’t valid in the world of real numbers. On the other hand, expressions like
or
are perfectly valid.
Even though expressions like or
are technically valid, it’s very uncommon to see them. Conventionally, people only use roots with degrees which are positive integers. The convention is to express the rest as exponentiation operations using the last exponential property I showed you:
For example:
As for the usual properties, this operation isn’t commutative:
For example:
It’s also not associative:
For example:
It only has a right identity element equal to 1:
And it has no inverse elements.
Logarithms
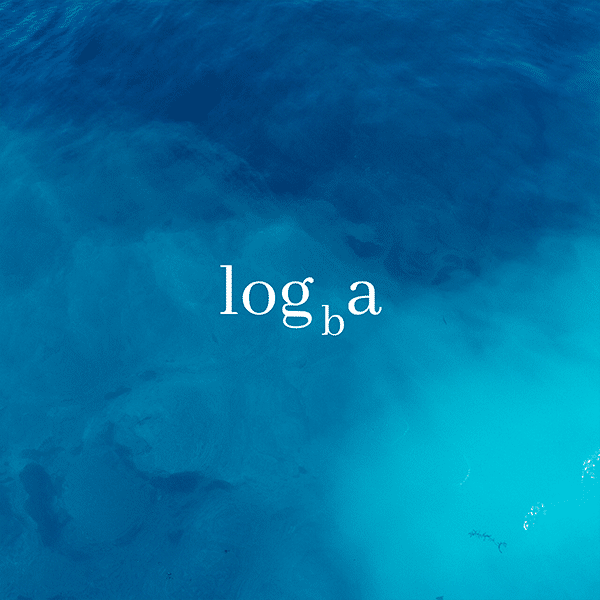
Like with roots, the validity of logarithms for numbers is directly related to exponentiation. First, the base cannot be 0 or 1 because those two numbers raised to any power return themselves. That is, for any a, and
. Which means expressions like
and
are undefined.
The case for negative numbers is interesting. Normally, the convention is that logarithms don’t work with negative numbers (both as the base or as the number whose logarithm we’re taking). Meaning, logarithms like and
are undefined. Now, technically, you could say something like
but you’ll rarely see such expressions. The reason is related to the fact that mathematicians want to treat the logarithm as a continuous function. I’m going to tell you more about this in my upcoming posts about functions.
Like roots, logarithms are not commutative:
For example:
They are also not associative:
For example:
Finally, the logarithm doesn’t have left nor right identity elements. In other words, there are no unique numbers l or r for which either of the following identities holds for an arbitrary real number a:
Consequently, there are no inverse elements for this operation either.
More logarithm properties
So, here’s a cool logarithmic property which allows you to switch the two numbers in the operation:
That is, the logarithm of b (base a) is equal to the multiplicative inverse of the logarithm of a (base b).
Another property is related to expressing a logarithm in terms of an arbitrary new base:
In words, if you have a logarithm of a number b with a particular base (a) and you want to express it in terms of another base (c), you do this by dividing the logarithm of b by the logarithm of a (using an arbitrary new base c).
Finally, I want to show you a nice property which is often used for simplifying logarithms:
In words, if the argument of the logarithm is raised to a particular power, you can take that power out of the logarithm by multiplying it by the logarithm of the argument alone.
A special case of this property in which is:
Properties involving more than one operation
In this final section, I want to show you some very important arithmetic properties that concern more than one operation. These are properties that, in a way, relate operations to each other.
Distributive arithmetic properties
As a reminder, for an arithmetic operation to distribute over another operation
on the left means:
And to distribute on the right means:
And if it distributes both on the left and on the right, we simply say that
Now, of the seven arithmetic operations we’ve looked at, which pairs do you think have this property (left, right, or both)? If you like, before you continue reading, take some time to try out a few pairs yourself.
The distributive property of multiplication over addition and subtraction
The first interesting relationship is between multiplication and addition/subtraction. Multiplication distributes over both on the left since, for any real numbers a, b, and c:
And it distributes over both on the right:
Which means the distributive property exists. The common name for it is the distributive property of multiplication over addition (or subtraction). This is one of the most important distributive properties which I’ve already talked about and used in a few previous posts (for example, when deriving the mean and variance formulas of the binomial distribution).
Try it out by plugging in some actual numbers for a, b, and c!
The distributive property of division over addition and subtraction
A very similar property is that of division over addition and subtraction. However, because division isn’t commutative, this property only exists on the right:
But not on the left:
I deliberately used the
Again, try it out with a few actual numbers to verify that it works!
The distributive property of exponentiation over multiplication and division
Here’s another distributive property that only exists on the right. Namely, the right distributive property of exponentiation over multiplication and division:
But it doesn’t exist on the left:
If you can’t immediately see why these distributive properties translate to the expressions above, let’s temporarily use the
The distributive property of roots over multiplication and division
Finally, the root operation also distributes over multiplication and division only on the right:
Of course, you need to be careful since this property only holds when both b and c are non-negative numbers.
The left distributive property doesn’t hold here:
Any other distributive properties?
Do any of the other possible pairs of operations have the distributive property? Well, it turns out the answer is no.
For example, if you tried to find a distributive property of addition over another operation (like multiplication), you’ll find that it doesn’t exist neither on the left nor on the right:
How about multiplication over division? Or Logarithms over subtraction? Or any of the other possibilities? Feel free to try out a few of them to verify that they don’t hold.
Well, actually the distributive property is a much more general concept in mathematics which exists between other types of operations working with mathematical objects other than numbers. But this is a topic for future posts.
Exponential and logarithmic properties relating addition and multiplication
To conclude this section (and the post itself), I want to show you a few arithmetic properties concerning exponentiation and logarithms. These are technically considered properties of these operations but, as you’ll see, in a way they are actually properties that subtly relate the operations addition and multiplication, as well as their respective inverses, subtraction and division.
Relating addition and multiplication through exponentiation
So, here’s the first fundamental property:
In words, if you raise a number (c) to the power of a sum of two numbers (a and b), this is the same as multiplying c raised to the power of a by c raised to the power of b.
To look at this property from a slightly different point of view, let’s use the notation again to express it as:
Notice that this almost looks like a left distributive property! The only difference is that the addition in the left-hand side became multiplication in the right-hand side.
If we combine this property with the property of exponentiation I showed you earlier, we can derive an analogous property that involves subtraction and division:
And with the alternative notation:
This also looks very much like a left distributive property, except the subtraction in the left-hand side became division in the right-hand side.
Relating addition and multiplication through logarithms
Now let’s look at a related (and equally important) property involving logarithms:
In words, the logarithm of the product of two numbers is the sum of the logarithms of those numbers (with the same base).
Let’s temporarily use the symbol to express logarithms as
. With this notation, the last property becomes:
This looks very much like a right distributive property, except the multiplication on the left became addition on the right.
And, using the logarithmic property , along with the exponential property
from earlier, we can derive another useful logarithmic property:
Or, with the alternative notation:
You see that this also looks like a right distributive property but the division operation on the left becomes subtraction on the right.
The deeper meaning of these relationships?
Let’s look at the properties we just discussed once again. Here are the two exponential properties:
And here are the two logarithmic properties:
It looks like exponentiation and logarithms somehow translate addition to multiplication and vice versa. They similarly translate the inverses of these operations (subtraction and division) to each other.
Now, in this context, also remember the properties from earlier:
It looks like, in a way, exponentiation and logarithms also relate additive inverses to multiplicative inverses somehow, don’t they?
Well, overall it seems like all these exponential and logarithmic arithmetic properties are telling us about a deeper relationship between all these operations. But does such a relationship really exist?
Yes, it does. And it is a fascinating one. For now, I’m going to let you think about this on your own. But we’re going to explore these deeper relationships in more detail in the next posts, as well as in future posts outside of the current series.
Summary
The main focus of this post was on the properties of the common arithmetic operations:
- Addition
- Subtraction
- Multiplication
- Division
- Exponentiation
- Roots
- Logarithms
The main arithmetic properties
Initially, I introduced the main types of properties at an abstract level with the general operation . Let’s summarize them here.
First, I showed you the commutative property:
And the associative property:
I also talked about the left (l) and right (r) identity elements:
As well as just the identity element (e) (when both the left and the right ones exist and are the same number):
Finally, there’s the inverse element property, which says that, for operations that have an identity element (e), a number a has an inverse element b, such that:
Here’s a table that summarizes these properties for the seven main arithmetic operations:

I also briefly mentioned the relationship between inverse elements and inverse operations. Namely, if e is the identity element of an operation, is the inverse operation, and a and b are numbers which are inverses of each other:
Other than those, I showed you a few properties specific to exponentiation:
As well as the following properties specific to logarithms:
Furthermore, I gave you some basic intuition for why operations aren’t always valid for every possible pair of real numbers. You can see these constraints in the sections specific to each operation but we’re going to revisit this topic in the next posts of the series.
Properties relating operations
I also talked about arithmetic properties that relate operations to each other.
The main class of properties I talked about were the so-called distributive properties. Or, more explicitly, the distributive property of an operation over another. That is, if we have two operations, and
, then
has the left distributive property over
if:
And
And if both the left and the right distributive properties hold for a pair of operations, we simply call that the distributive property of the first operation over the second operation.
Here’s a table that summarizes all existent and non-existent distributive properties:

Each row represents the operations over which the row’s operation distributes. For example, the third row shows that multiplication distributes over addition and subtraction. A ‘Yes’ means both the left and right distributive properties hold, whereas a ‘No’ indicates that neither hold. A ‘Right’ means that only the right distributive property holds.
Finally, I showed you specific arithmetic properties of exponentiation and logarithms which almost look like distributive properties. They aren’t really distributive properties, however.
Here are the exponential properties I’m talking about:
And here are the logarithmic properties:
They almost look like left and right distributive properties, except the operation over which they “distribute” over turns from addition/subtraction to multiplication/division or the other way around. And I told you that these particular properties reveal a deeper relationship between these operations which I’m going to talk about in future posts.
The rest of the series
In the beginning of the introductory post of this series, I started the entire discussion with a short introduction to mathematical Platonism. Which is the view that mathematical objects (like numbers) are abstract objects that have independent existence and no direct causal relationship with the physical world. A view inspired by the ideas of the ancient Greek philosopher Plato in his work Theory of Forms.
But I also told you that one of the main goals of this series is to explore the intuitive relationship between these abstract objects and the physical world we live in.
Now let’s temporarily forget everything we know about numbers and arithmetic and let’s try to rediscover these concepts from scratch by relating them to things we’re familiar with in the physical world.
But remember! Mathematics doesn’t have to relate to the physical world. It has its own existence and it doesn’t care about us. We are the ones who care about it because we want to study the properties of abstract mathematical objects. And we want to do that because:
- It helps us infer things about properties of objects in the physical world.
- We are simply curious and fascinated by them for no particular practical reason.
Well, in the next post of this series we’re going to begin our journey into the world of Mathematics by dropping any existing assumptions. And we’re going to reconstruct the part of this world related to natural numbers and arithmetic.

Leave a Reply