Hi, everyone! Today’s post is the introduction to a new mini-series on numbers and arithmetic.
In this series, I’m going to take you back to some elementary math concepts from your childhood. I want you to get a good intuition about fundamental mathematical objects which we use in pretty much everything else we do in math. Namely, the objects called numbers.
Besides numbers themselves, I want to focus on the intuition behind the most common operations with numbers: addition, subtraction, multiplication, division, exponentiation, roots, and logarithms. The field concerned with these operations is called arithmetic and is one of the fundamental fields in mathematics.
To build intuition for something usually means relating it to things we already have intuition for. So, my goal here is going to be discussing how we can relate the concepts of numbers and operations with numbers to concepts in the physical world we’re familiar with.
In this series, I’m going to focus on the set of real numbers. This isn’t the biggest number set and I will definitely talk about others (notably, complex numbers) in future posts.
Overview of the series
The titles below will become active links as I finish the posts:
- Properties of arithmetic operations
- Natural numbers
- Negative numbers and integers
- Fractional and rational numbers
- Irrational numbers
In the current post, I’m going to give an overview of the different subsets of real numbers and the operations we perform with them. I’m not going to go into too many details and I’ll leave the main intuition and proofs for the dedicated posts above.
In other words, today’s introductory post’s aim is to give the big picture of numbers and arithmetic operations. In the next post, I’m going to show an extensive list of the properties of arithmetic operations. And, as the series progresses, in the following four posts we’re going to gradually fill the missing details, proofs, and the intuition behind the different types of numbers and operations between them.
Table of Contents
Discovering the world of Mathematics
For billions of years, millions of species have been evolving from the earliest replicator objects (molecules). And sometime around 200 thousand years ago came we, humans.
In many respects, we’re quite similar to other species, especially mammals. And especially the subset of mammals called primates with whom we share a common ancestor in the evolutionary tree. In absolute terms, our similarities are far greater than our differences.
But one of the remarkable differences between humans and all other animals lies in our outstanding ability to do abstract thinking. Well, it’s precisely this ability that gave us access to the abstract world of mathematics. It is the reason why we even know of its existence!
We first discovered this fascinating world quite recently. Our first encounter was less than 5000 years ago, which is a small fraction of human history. When we first discovered it, it was all a big dark forest. We saw a tiny fraction of that world and we didn’t even know its true size. But we were so fascinated by it that we’ve been studying it ever since. We’ve been uncovering more and more of it. We’ve been drawing maps and building theories about it, making many previously dark patches visible.
Well, this journey continues to this day. And it will probably (and hopefully!) never end. But why am I calling mathematics a “world”?
Mathematical Platonism
Imagine for a moment a completely different world than the one we live in. A world where there are no atoms, no molecules, no living beings… Only mathematical objects. It is an abstract and idealized world which has an existence of its own: the world of Mathematics.
This is a world first described by the great ancient philosopher Plato who, roughly speaking, postulated the existence of 2 distinct “realms”:

- The physical world which we experience through our senses
- The ideal world of abstract objects (which mathematics is a part of) that don’t occupy space, change with time, or have a causal relationship with the physical world.
In his Theory of Forms, Plato considered the objects in the physical world (like rocks, chairs, squares, and triangles) to be imperfect imitations of objects in this ideal world.
Now, I don’t want to get too much into Platonism. And Platonism certainly isn’t the only philosophical understanding of mathematics out there. But, at least for this series, let’s go with it, even as a mere metaphor.
Modern mathematical Platonism gets its inspiration from Plato’s Forms but it’s not necessarily constrained by all of Plato’s original ideas. In a nutshell, it postulates these three general properties of mathematical objects:
- Existence — every mathematical object has its own existence.
- Abstractness — mathematical objects don’t occupy space, don’t change with time, and don’t interact with the physical world (they have no causal effects).
- Independence — mathematical objects exist independently of the minds of people or any other intelligent beings who can think of them.
The ideal objects in the world of mathematics are things like numbers, functions, and geometric figures. And in this series I want to specifically focus on the intuition behind numbers and the operations we perform with them.
Numbers
So, what is a number? Well, we already said numbers are abstract mathematical objects with certain properties. We typically use them for things like counting objects or measuring properties of objects in the physical world. For example, the number five can represent five apples (count) or the height of a five-meter tree (length).

We typically use numerals to represent numbers. Those are specific symbols like 3 (to represent the number three), 22 (for the number twenty-two), and so on. These, of course, are examples of the most commonly used Arabic numeral system, which we’re going to be using here as well.
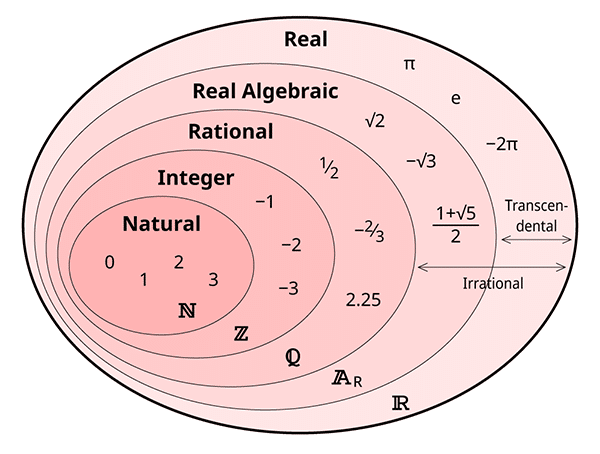
Numbers can be classified into different categories or classes called sets. The most famous of these sets are the natural numbers, the integers, the rational numbers, and the irrational numbers. The irrational numbers themselves can be classified into the subcategories of algebraic numbers and transcendental numbers.
- Natural numbers are non-negative whole numbers: 0, 1, 2, …
- Integers are the natural numbers and their negatives: …, -2, -1, 0, 1, 2, …
- Rational numbers are the set of all fractions where both the numerator and the denominator are integers:
,
,
, …
- Irrational numbers are all numbers which aren’t… rational.
Anyway, together all these types form the set of real numbers:
Real numbers are ubiquitous in mathematics and probability theory in particular. Well, probabilities themselves are real numbers too! But the presence of numbers in probability theory is far more significant. The first time I seriously discussed them was in my overview post on discrete probability distributions. There I showed you that you can think of discrete sample spaces as subsets of natural numbers, whereas continuous sample spaces are subsets of real numbers.
Arithmetic (operations with numbers)
In the context of mathematics, an operation is something that takes one or more mathematical objects and does something to them to produce another object. When the operation works with exactly one object, it’s called a unary operation and when it works with exactly two objects, it’s called a binary operation. These two are the most important arithmetic operation types and in this series I’m only going to consider them.
Often, but not always, operations are represented by a special symbol, like . For example, a unary operation looks like:
And a binary operation looks like:
Furthermore, the result of an operation is typically given after the equals sign (=):
Here a and b are the mathematical objects on which the operation is applied, whereas c and d are other mathematical objects which are the results of the operations.
As you can probably guess, the operations we’re going to look at here are the ones concerning the objects called numbers.
The main arithmetic operations
Addition, subtraction, multiplication, and division
Most of you are probably well familiar with the four basic arithmetic operations you can apply on real numbers: addition (), subtraction (
), multiplication (
), and division (
). All of them are examples of binary operations.
You can think of addition and subtraction as opposite operations:
Just like you can think of multiplication and division as opposite operations:
For multiplication and division, there are two common alternative notations which I personally prefer:
The last one can also be viewed as a fraction, which I’m going to talk about in more detail in the post on rational numbers.
Unary operations
An example of a unary operation is the additive inverse of a number which simply reverses the number’s sign from positive to negative and vice versa. It has the same symbol as the one for subtraction:
When you apply this operation on (say) 3, it will produce -3. And when you apply it on -3, it will produce 3.
Another example of a unary operation is the absolute value of a number, denoted by two vertical bars. If the number itself is positive, the absolute value operation returns the number itself and if the number is negative, it returns its positive version. For example:
Finally, the third main unary arithmetic operation is the multiplicative inverse of a number, which is simply 1 divided by the number. For example, the reciprocal of 2 is
Exponentiation
You’re also likely familiar with the exponentiation operation which is another binary arithmetic operation:
It’s typically defined as “repeated multiplication” in elementary arithmetic classes. You can read an expression like
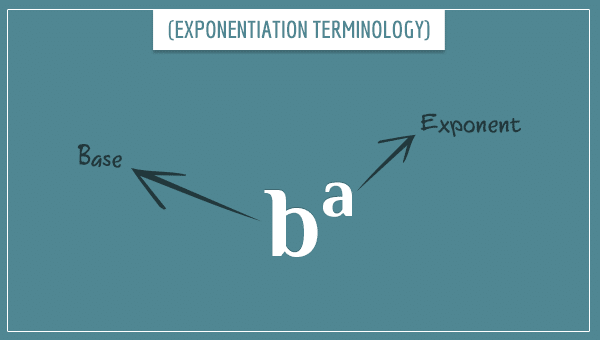
Notice that the notation here is a little different in that there’s no special symbol for this operation. Rather, the second number is written in the top right corner of the first. This is simply the established convention. We could have easily defined a symbol to represent this operation as well. For example, we can define the symbol to mean “raise to the power of”:
But again, the convention is what it is. Just know that there can be different types of notations for expressing an operation. What’s important is its definition.
Inverse operations
I already showed you that addition-subtraction and multiplication-division are inverse operations. But what exactly does that mean?
Well, notice what we’re really doing. For example, when we add the numbers 2 and 3, the result of this addition operation is 5. Then, when we take the result and apply the inverse of the addition operation on it with any of the numbers we added, we get the other one:
Similarly, when we multiply the numbers 2 and 3, the result is 6. And when we apply division (the inverse of multiplication) on the result with any of the numbers, we get the other one:
Intuitively, you can think of the inverse operations as answering questions in the form:
- What number should I add to 3, in order to get 5? (the operation
)
- What number should I multiply by 3, in order to get 6? (the operation
)
The inverse of exponentiation
What about exponentiation? Does it also have an inverse operation? For example, for what is the operation that we can apply on 8 and one of the numbers to get the other?
Actually, exponentiation has two inverse operations!
The first is the so-called root operation. The notation here is , where a is the result of raising a number to a power and b is the power itself. For example:
Which you read as “the 3rd root of 8”. This operation answers the question:
- What number should I raise to the 3rd power, in order to get 8?
A special case for this notation is when the power is 2, in which case it’s simply omitted:
But we can also ask another question:
- To what power should I raise the number 2, in order to get 8?
The name of this second inverse of exponentiation is the logarithm. It’s not very common to call a logarithm an operation, but essentially it is. Here’s the notation:
The bottom number in the log is also called the base of the logarithm (since that would be the base of the inverse exponentiation).
Like with roots, there’s a special convention to omit the base when it’s 10. For example:
Again, don’t be confused by the notations for these operations. We could have just as easily defined random symbols to represent them in the typical way, like:
Why does exponentiation have two inverses?
You might be wondering why addition and multiplication have a single inverse operation but exponentiation has two different ones. Well, the answer to this question lies in the properties of these operations.
There’s an inherent symmetry in addition and multiplication:
Both a and b are terms that are being added to each other or terms that multiply each other. On the other hand, in exponentiation you have a number that is raised to a power and a number which is the power itself – two qualitatively different roles.
In other words, the above symmetry doesn’t exist with exponentiation:
This property that addition and multiplication have but exponentiation doesn’t is called the commutative property and it’s one of the topics of the next post in this series.
Expressions involving more than two numbers
You can also apply these operations on more than two numbers. When the order is important or ambiguous, you typically use parentheses to indicate it. For example:
You can have operations with as many numbers as you want. When necessary, you can put parentheses within parentheses:
Often, for readability purposes, people use different types of parentheses for the outer ones, like square brackets or curly brackets (especially when the expressions are very long and convoluted):
Basically, parentheses and brackets indicate that the operation inside them should be performed with priority and the result used as a single number (inner parentheses first, outer ones last).
There are also certain conventions for a particular order when there are no parentheses. For example, multiplication has a higher priority than addition. An expression like by default means
. This convention is so firm that often the multiplication operation is expressed with no symbol at all:
Of course, you can only do this when you’re working with letters (representing numbers). Otherwise, it would be ambiguous whether
Similarly, the exponentiation operation has an even higher priority than multiplication. For example:
These conventions have been established in order to make mathematical expressions more readable by reducing the need for too many parentheses or brackets.
Summary
In this introductory post, I briefly mentioned the set of real numbers and its main subsets: natural numbers, integers, rational numbers, and irrational numbers. I introduced them as “objects” existing in the abstract “world of Mathematics” — an idea inspired by Plato’s Theory of Forms.
I also talked about mathematical operations which are part of the field called arithmetic. More specifically, I introduced you to the concepts of unary and binary operations. Unary operations are ones that work with only one number, whereas binary operations work with exactly two numbers.
The specific arithmetic operations (and their corresponding notations) I talked about were:
- addition (
)
- multiplication (
or
)
- exponentiation (
)
And their corresponding inverse operations:
- subtraction (
)
- division (
or
)
- roots (
) and logarithms (
)
The inverse of an operation is simply one which takes its result and one of its terms to produce the other. More explicitly, say is the symbol of an operation and
is the symbol for its inverse operation. Then, if we have:
it follows that:
or:
Commutative (symmetric) operations have only one inverse operation, whereas non-commutative operations have two different inverse operations. You’ll read more about the commutative property in the next post.
Finally, I talked about parentheses and brackets ((), [], and {}) as a special notation for specifying priority of operations in expressions involving more than two numbers. But I also mentioned that, by convention, certain operations have a priority over others. For example, multiplication has priority over addition and exponentiation has priority over multiplication:
Final words
Well, this is it for today. I know most of you were probably already familiar with these concepts but you still might learn a few new things about them as this series progresses. And I’m sure many of you will at least gain some deeper intuition about the concepts that will make you see them in a different way than before.
Feel free to leave any remarks or questions in the comment section below.
I’ll see you in the next post!
Thanks for your efforts. I love math more. Hope there will be a series on linear algebra. 🙂
Thanks for your feedback Younghoo! Oh yes, there is going to be a series on linear algebra. As a matter of fact, I have been working on a serious plan as well as drafting of many posts in the past couple of months. There is going to be an announcement soon!
Greetings,
I would like to thank you for this series, it has been very useful and change the way in which I saw many concepts. I’m very interested in the post about ‘Fractional and rational numbers’, when will you publish it?
Thanks for all.
Thank you for the nice words, Max! Due to some unexpected circumstances, I haven’t been able to devote too much time to the website in the last year, but I am actively working on getting back to writing. The draft for the Fractional numbers post is in fact about half ready. I am hoping to get back on schedule soon.
Cheers
Hi there: any update on when you will be able to finish the series? It’s been a year since your last post – just curious. Also, I hope that whatever kept you from devoting time to the series has resolved. Christopher