Why do people flip coins to resolve disputes? It usually happens when neither of two sides wants to compromise with the other about a particular decision. They choose the coin to be the unbiased agent that decides whose way things are going to go. The coin is an unbiased agent because the two possible outcomes of the flip (heads and tails) are equally likely to occur.
Mathematically, this is expressed as:
But think about it. Have you ever bothered to check if heads and tails are really equally likely outcomes for the coins you flip? Actually, no real coin is truly fair in that sense. One side is always slightly heavier or bumpier than the other. This biases the coin away from the ideal 50/50 ratio of heads and tails.In fact, the coin flipping process itself can slightly skew even an ideal coin’s outcomes. In their SIREV paper, authors Persi Diaconis, Susan Holmes, and Richard Montgomery analyze the math and physics behind the process of coin flipping. Here’s an excerpt from their abstract (you can find the original pdf here):
We analyze the natural process of flipping a coin which is caught in the hand. We prove that vigorously-flipped coins are biased to come up the same way they started. […] For natural flips, the chance of coming up as started is about .51.
Table of Contents
Introduction
Whether this kind of a bias is a problem in the real world is a separate question. However, if you decided to gamble on coin flips, you can be sure it will have a dramatic effect on your long-term wins when the number of flips grows significantly. For example, if a coin comes up heads with probability 0.51 (instead of 0.5), after 10000 flips the expected number of heads is going to be 5100. This is 100 more than the expected number of a perfectly unbiased coin.
Okay, maybe you don’t ever intend to gamble with coins. And you don’t care if any coin is biased or not. However, thinking about the process of estimating a coin’s bias is very useful in itself. You can apply analogous methods to all sorts of problems that you do care about.
In this post I’m going to show a way of estimating the bias of a coin using Bayes’ theorem. The method relies only on empirical data collected by flipping the coin multiple times. It isn’t concerned with any of the physics behind individual flips.
Instead of flipping a real coin and reporting its outcomes, I’m going to simulate coin flips with the programming language MATLAB. I’m not going to discuss any of the code here but if you’re into programming you can download it and run your own simulations. You don’t need to be into programming to be able to follow the rest of the post, however.
In the actual simulation, I’m going to use Bayes’ theorem to recalculate the estimate of a coin’s bias after every flip. But before I do that, I’m going to introduce the concept of probability distributions which is going to be helpful along the way.
10/21/2019 Update: Besides MATLAB, the code is now also available in Python and Excel.
Probability distributions
For a deeper introduction to probability distributions, check out my post dedicated to this topic.
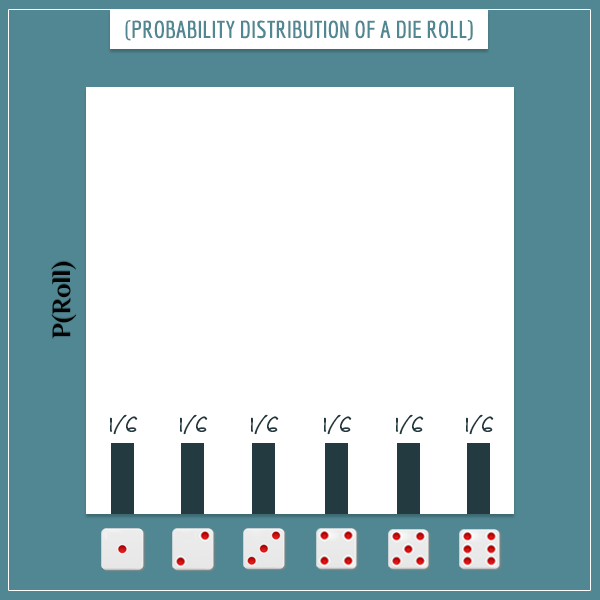
Imagine you have a random process with multiple possible outcomes. An example is rolling a six-sided die, where the 6 possible outcomes are the numbers 1 through 6.
The sample space of a random process is the set of these possible outcomes. Each outcome has a particular probability. If you remember from my post about sample spaces, the probability of the entire sample space is equal to 1 because, with complete certainty, at least one of the possible outcomes will occur. The exact way this total probability is distributed among the possible outcomes is called a probability distribution.
Think about the die rolling example again. Assuming the die is perfectly unbiased and each outcome is equally probable, you divide the total probability (1) to six equal parts and the probability of each outcome becomes 1/6:
A random process can have any number of possible outcomes. A probability distribution only requires that the sum of all probabilities adds up to 1 — neither more nor less. This suggests that anytime you adjust the probability of one outcome, this will be “at the expense of” the probability of at least one of the other outcomes.
For example, if it turns out that the die is unfairly biased to come up 6 with probability 0.4 (instead of 1/6), the remaining 5 outcomes only have a total probability of 0.6 to distribute among each other.
Probability distributions and uncertainty
A probability distribution is a more general concept. It describes the uncertainty in a random process (like rolling a die). For example, before you roll the die, you’re uncertain about which side will be facing up because the process is random and each outcome will occur with some probability (which is specified by the probability distribution).
But what if you’re also uncertain about the probability distribution itself? You don’t have to assume that the die is fair and each outcome’s probability is 1/6. You can actually assign probabilities to the possible candidates for the die’s real probability distribution. This way you have a probability distribution for the possible probability distributions! Things are getting deep.
The bias of a coin
In this section, I’m going to illustrate the last concept with a simulation. However, instead of a die, I’m going to use a coin because having only two possible outcomes will make calculations much simpler.
Most coins are close to being fair. That is, they have the same probability of landing heads and tails (0.5). You can talk about the bias in terms of only one of those probabilities.
There are only two possible outcomes and the other probability has to be 1 minus the first. Therefore, specifying the bias of a coin actually specifies the entire probability distribution. This distribution is called the Bernoulli distribution. If you want to learn more about it, check out my post dedicated to it.
From now on, I’m going to measure the bias as the probability with which it lands heads:
Representing the bias mathematically
With the above definition, a fair coin is one for which Bias = 0.5. Most coins may not be perfectly fair but their bias is still very close to 0.5 and deviations are hard to detect “with a naked eye”.
Imagine that there’s this special coin factory which produces coins having all sorts of biases. Meaning, if you pick a random coin from the factory, its bias can be any number between 0 and 1.
But to make things even simpler, assume that the possible biases are only the 101 discrete values between 0 and 1:
- 0, 0.01, 0.02, 0.03, …, 0.98, 0.99, and 1.
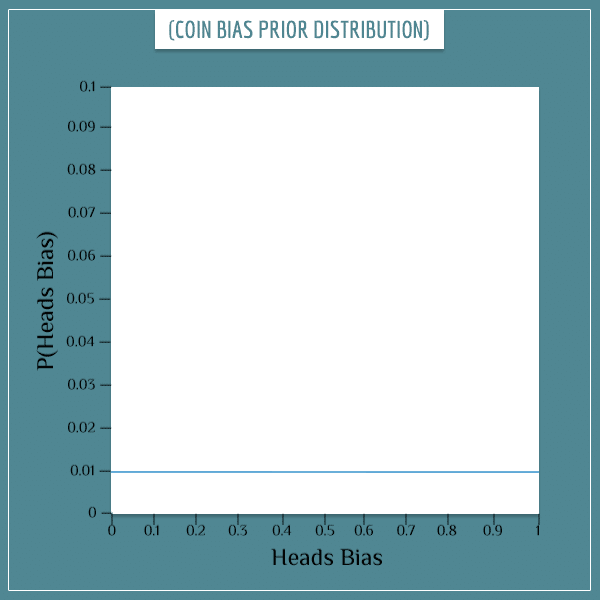
You have no reason to assume that a randomly picked coin is more likely to have any of the 101 values compared to the rest. Therefore, you start your estimation of the bias by assigning it a uniform prior distribution:
In order to not clutter the x-axis too much, I didn’t put all possible bias values in its label. But the blue line you see in the plot is supposed to be a series of 101 dots positioned very close to each other. The height of each dot (the y-axis value) represents the prior probability of the corresponding “Heads Bias” value.
In this case, the probability of each bias is 1/101 (this follows from the requirement that the probabilities in any distribution must add up to 1). Calling the prior distribution uniform is another way of saying that all biases are equiprobable.
Parameters and parameter estimation
Parameter is a term in probability theory used for referring to characteristics of a system, such as the bias of a coin. A parameter is simply a feature or a property of the system.
Parameter estimation is inferring the value of a parameter from new data about the system (read more in my post on Bayesian vs. Frequentist approaches to statistics).
In the next section, I’m going to reverse things and first show a simulation in which the bias of a coin (drawn from the special coin factory I mentioned above) is estimated with Bayes’ theorem. In the final section, I’m going to explain some of the technical details of the simulation.
Coin bias simulation
Say someone randomly drew a coin from a pile produced by the factory. The coin’s bias happens to be:
However, you don’t know this yet. The person hands you the coin and asks you to estimate its bias. If you want to do this by using Bayes’ theorem, you would flip the coin many times and use the outcomes to update the probability of each possible value of its bias. In other words, after each flip you would update the prior probability distribution to obtain the posterior probability distribution.
Then you would make the posterior distribution your next prior distribution and update it with the next coin flip. The idea is to repeat this procedure a sufficient number of times until you’ve gotten a “good enough” estimate of the coin’s bias. How good is “good enough” depends on you and your goals.
Results
Let’s get down to business. See what happens to the posterior distribution after the first 500 flips (click on the image to start the animation):
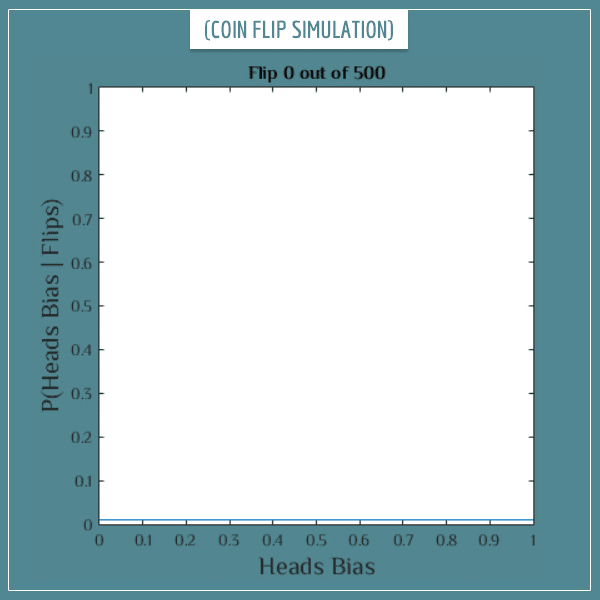
So, after 500 flips most of the probability gets distributed around the value 0.3. In fact, the probability for most other values virtually disappeared — including the probability of the coin being fair (Bias = 0.5). This already is a pretty good estimate of the real bias!
But you might want an even better estimate. If you’re really determined to find the true bias of this coin, you can continue flipping it. Just keep flipping until you’ve reached the precision that satisfies your goals. See what happens after a set of 15 000 additional coin flips (again, click on the image to start the animation):
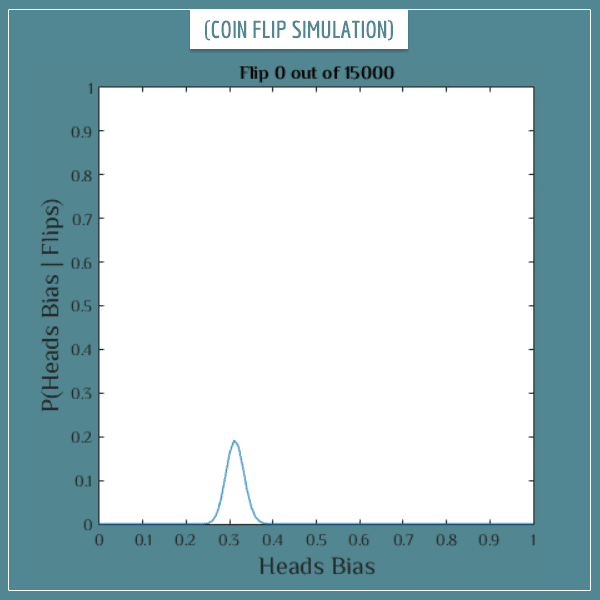
Well, now you can be almost certain the bias is either 0.3 or some value very close to it! You see that, as you accumulate more data in the form of coin flips, you get closer and closer to the real bias of the coin.
Now it’s time to dig into the details of the simulation.
Explaining the simulation
As I said in the beginning, you can download the code for this simulation and run it yourself with different values for the coin bias parameter. The code is written in MATLAB and is only 30 lines long. Here’s what it does:
- Creates an array of 101 numbers which represent the prior probabilities of the 101 possible bias values. Each probability is set equal to 1/101.
- Selects a bias for the imaginary coin (you can change this part).
- Generates a random number between 0 and 1 and counts it as “heads” if it’s less than or equal to the value of the bias, and counts it as “tails” if it’s greater than the bias. This is one imaginary coin flip.
- By applying Bayes’ theorem, uses the result to update the prior probabilities (the 101-dimensional array created in Step 1) of all possible bias values into their posterior probabilities.
- Repeats steps 3 and 4 as many times as you want to flip the coin (you can specify this too).
There are also a few code lines that dynamically plot the updated probabilities (like the animated plots you saw in the previous section). Now the only thing left to explain is Step 4.
Updating the prior probability distribution with Bayes’ theorem
If you haven’t already, I suggest you take a look at my post explaining the intuition behind the rule. It’ll help you understand any parts from this section you potentially get stuck on. Also, you can take a look at another post where I show all the steps of the calculations with another example.
Say you’re currently updating the probability of the bias being 0.5 and you just flipped heads. The equation for updating the prior into a posterior probability is:
Explaining the terms of the equation
- P(Bias=0.5): The prior probability that the bias is equal to 0.5. Initially, it’s 1/101.
- P(Bias=0.5 | “Heads”): The posterior probability (or the next prior probability) is the updated prior probability after taking into account the result of the flip.
- P(“Heads” | Bias=0.5): The likelihood term represents the probability of flipping heads, if the coin’s bias is 0.5. Well, by definition, that probability is equal to 0.5. If the result is tails instead, the likelihood will again be equal to 0.5. But if you were estimating any other piece of the probability distribution of the bias, the two would differ. For example:
- P(“Heads” | Bias=0.8) = 0.8
- P(“Tails” | Bias=0.8) = 0.2
- P(“Heads”): The evidence term is the overall probability of getting heads and is the sum of all 101 (prior * likelihood) products. You can think about it as the expected probability of getting heads on the current flip. This term has the same value for all biases.
So, this way you calculate the posterior probabilities for all values between 0 and 1. Then you flip the coin again and repeat the calculations but this time with the posterior distribution as the next prior distribution. As you collect more data, your estimate of the bias will get better and better and you can get arbitrarily close to the real value.
Well, as long as you have motivation to continue flipping the coin.
Summary
In this post I introduced two new concepts from probability theory:
- Probability distribution: a particular assignment of probabilities to all possibilities of an uncertain process
- Parameter estimation: the process of narrowing down the possible values of a parameter of a system from data generated by the system
In particular, I demonstrated the use of Bayesian parameter estimation. Even though estimating the bias of a coin is a very simple problem, once you intuitively understand the technique, the generalization to more complicated problems isn’t difficult.



Very nice simulation. Thanks.
I was unable to download the Matlab code for the simulation. Might you have one available as a text or MS Word document? Thanks!
Hi YF, I’m glad you liked the post! You can access the file in txt format here.
Many thanks! Your site is very helpful and I appreciate the work and thought you have put into it; I will be recommending it to others.
How would I then use the posterior to calculate how many heads I can expect to see in 10k flips?
That’s a good question, Mattias!
The easiest thing you can do is take the mean of the posterior distribution (called the maximum a posteriori estimate, or MAP) and use it as the proportion parameter (p) of a binomial distribution. And of course use 10000 as the n parameter of the distribution. Then the expected number of heads would be the mean of the binomial distribution itself, which is equal to p*n.
In other words, if the mean of the posterior distribution is, say, 0.55, based on this analysis you would expect about 5500 heads in 10k flips.
This isn’t the best way to do it, however. Notice that this estimate doesn’t take into account the full posterior distribution. So, if the posterior is too wide or skewed, your estimate based on the MAP wouldn’t be as accurate.
A better approach (though computationally more expensive) would be to have a separate binomial distribution for every possible value of the bias of the coin and take the weighted sum of those distributions, where the weights are the probabilities of the respective biases. For example, for simplicity let’s assume that the only possible biases for the coin are:
– 0.25, with a probability of 0.3
– 0.5, with a probability of 0.4
– 0.75, with a probability of 0.3
Then you would have 3 binomial distributions, each with the same parameter n=10000, but where the p parameter is 0.25, 0.5, and 0.75. Then you would multiply each distribution by 0.3, 0.4, and 0.3 (respectively) and take the sum of the 3 weighted distributions. Finally, you take the mean of the resulting sum of distributions as your estimate for the number of heads in 10k flips.
I realize that I am skipping some details here, but please let me know if this makes sense to you. Feel free to ask any clarifying questions, including about the details.
Great article, The Cthaeh could you elaborate on the R Code ( I am not verse in R) the Likehood function isn’t implementing a binomial distribution or something closed to this? My understanding was that we should not touch the Likehood function but focus on the prior – which is narrowed after each experiment, (a MLP kind of thing opposed to a MLA) – this is the kind of application of Bayes approach I was looking. Please advice I the following reasoning should also lead to the correct response but with tackling only the prior. I’ve done everything in Excel just to decompose each step.
1. I set up 340 coin toss experiment with bias 0.3 through the rand() function
2. I start with two column 1 with the range of bias the second with the starting probabilities (1/101)
next my idea was to start the experiment and write down the frequencies of the head proportion and correct the prior accordingly.
ex. 1 experiment % H: 0,31 second exp %H: 0,47 etc… this will create a probability distribution around 0,3 this probability distribution is plugged to the bayes formula
posterior : P(“Head”| Bias = x) = x * new_prior / sum (over all new_prior)
in my opinion this will converge to the 0,3 theoretical value probably very fast because the first experiments will eliminate all bias far away from 0,3.
I don’t know if I express myself clearly what I would like to obtain is a Bayes application which is only supported by adjustment of the prior the likehood stays the same all the time i.e like you wrote P(“Heads” | Bias=0.x) = 0.x no complicated formula as in R code:
likelihood = bias_range.^flip_series(k).*(1-bias_range).^(1-flip_series(k));
you see what I mean?
Hello, Imre! Thank you for asking this question, as it revealed to me some parts of the code that might indeed lead to confusion. Let me clarify.
First, a small correction: the code is in MATLAB, not R. Though the code wouldn’t look too differently even if it was in R.
Yes, you are absolutely right. The likelihood function shouldn’t change. And it doesn’t in the above code either. Let me explain step by step.
n = 15000; %Number of coin flips
This part of the code defines how many times the coin will be flipped in total. In my code, there are 15000 experiments where each experiment is a single flip. And the prior distribution is updated after each flip. You seem to have taken a different approach where you update the prior distribution after series of flips, after calculating the proportion of heads in each of them. This isn’t wrong, it’s just a different approach. It does require somewhat more complicated mathematics, however. In this case you will indeed need a binomial distribution, whereas in my code what is used is a Bernoulli distribution.
for k=1:n
This is a for loop which runs from 1 to n (15k) and at each iteration a new posterior distribution is calculated which becomes the prior distribution for the next iteration. Also, at each iteration the variable k will be a number between 1 and n. For example, on the 5th iteration k will be equal to 5, on the 146th iteration it will be equal to 146, and so on.
Now, the variable flip_series (which is defined before the for loop begins) is a sequence of 0’s and 1’s (where 1 represents “heads” and 0 represents “tails”). Therefore, the term flip_series(k) will be equal to 0 or 1 on each iteration (depending on whether the kth element of flip_series is 0 or 1).
The variable bias_range contains all 101 biases. So, the expression bias_range.^flip_series(k) simply raises all biases to the power of 0 or 1. To understand this more easily, assume for a moment that we’re doing this for only one of the possible biases and let’s replace bias_range with a new variable called bias. Then the expression bias.^flip_series(k) will be equal to bias (if flip_series(k) is 1) or to 1 (if flip_series(k) is 0). Are you with me so far?
On the other hand, (1-flip_series(k)) will be equal to the opposite of flip_series(k). That is, if flip_series(k) is 1, (1-flip_series(k)) will be 0, and vice versa. So, the expression (1-bias).^(1-flip_series(k)) will similarly be equal to (1-bias) or 1. This is really just a small mathematical trick to make the code shorter.
Notice then that at each iteration the expression
bias.^flip_series(k).*(1-bias).^(1-flip_series(k))
will be equal to either bias or (1-bias).
The expression with bias_range simply does this for the whole array of biases simultaneously. Otherwise, I would have needed a second for loop inside the first one, that runs over the 101 biases. This will still give the right result, but it’s less efficient.
Bottom line is that the complicated looking expression for the likelihood variable is a fancy and efficient way of making the likelihood equal to bias or (1-bias) at each iteration.
Does this make sense? Let me know if I managed to answer your question. And feel free to ask about anything that is still unclear to you. I would very much like this post to be intuitive to all readers, regardless of their programming background.
The Cthaeh, perfect now I am sync with you – my first guess was R I even look for some of the semantics with a mitigate success then I though that okay it’s maybe coming from some older version of R… just one question why are you interested in the (1 – bias) in the likehood and not only in the bias? In my approach I am only applying my “distribution” around 0,3 to the P(“heads”| bias= 0.x) I really try to stick to your text my formula is as follow:
Bias | Prob0. –start– –first sim—> Bias | Prob1.
. 0,09901 . 0,000
. 0,09901 . 0,000
0,29 0,09901 0,29 0,005
0,30 0,09901 0,30 0,089
0,31 0,09901 0,31 0,005
. etc… . 0,001
. . 0,000
sim (it’s a range of 0 1) = if rand() <= 0.3 then 1 else 0 [ simulating a biased coin toss with bias 0.3)
post_distr = bias .* prob0 /(sumproduct(bias*prior0))
then
post_distr = bias .* prob1 /(sumproduct(bias*prior1)) and so on… but may be what I am doing is is not a bayesian approach at all…
The likelihood function specifies the probability of obtaining the data, given a specific value for the bias parameter. In the case of a single coin flip, the data is a 0 or a 1, yeah? Well, you need to be able to specify the probabilities of both outcomes.
Let’s say the bias is 0.3. This means that for a single flip you have:
P(heads) = 0.3
P(tails) = 1 – 0.3 = 0.7
That is, the (1-bias) is simply the complementary probability. You need both, as you need your likelihood function to be able to specify the probabilities of all possible outcomes of the experiment (in this case, there is only 2 possible outcomes).
I am not sure I completely understand what your Excel sheet is doing. Could you give a more detailed and systematic description of your approach? Please list all the columns (and/or other lone cells) that you have, as well as their meaning and values/formulas. Don’t worry, I am going to help you get it right in the end!
By the way, in the meantime please take another look at the section Updating the prior probability distribution with Bayes’ theorem above. The formula I gave there is all you need to reproduce the calculation. After a single coin flip, you just need to apply it for all possible biases.
Let me help you with the first steps.
Let’s say in your sheet you have specified the bias of the coin to be 0.3. Then you generate a single coin flip using rand(). Let’s assume you happened to generate 1 (heads).
Now, let’s ask ourselves: what is the probability that the bias of the coin is, say, 0.72? You would calculate this posterior probability like this:
The right-hand side values are:
P(1 | bias=0.72) = 0.72 (if the outcome was 0 instead, this value would have been 0.28)
P(bias=0.72) = 1/101 (because you just started the experiment and all possible 101 biases have the same probability
P(1) = sum_over_x(P(outcome=1 | bias=x) * P(bias=x))
In the last term (the evidence), x takes all 101 possible values for the bias:
0, 0.01, 0.02, 0.03, …, 1
After doing all this, you just calculated the posterior probability of your coin’s bias being 0.72 (you would expect to get a low value here, since the actual bias of your coin is 0.3). To get the full posterior distribution, you just need to apply all these steps for the remaining 100 possible biases. And that concludes the process.
Then you can flip the coin again and repeat all the steps above. But this time, instead of having 1/101 as the prior probabilities, you would use the posterior distribution you calculated from the previous experiment instead. And then you can perform as many experiments as you like, each time updating the prior by following the steps above.
Does this help?
Thank you once more I just saw after posting my response that all the construction (columns etc..) in my illustration collapse in one unreadable text.
I am doing exactly what you’ve describe in your last post, and also in the formula I am not using the complementary probability (1 – bias) only “bias”.
A just update the prior with a bunch of coins toss in excel (340 at least) from which I compute a new probability distribution (a simple histogram of how much coin toss fall in the interval 0.01 – 1) once I have a new prior I plug it in your formula and so on. but… without bothering with (1-bias) only P(1|bias) i.e. my interval 0,01 – 1 multiply by my new “distribution” of prior coming from my repeated 340 experiments. I think that my likehood is managed “outside” in my 340 experiments and you have it in the formula that’s why you have bias and (1-bias) [I have if test < 0.3 then 1 – this is for bias, and else 0 – this is for the (1-bias) part]
Hey, Imre!
Yes, you do need the likelihood function to be able to account for all possible outcomes of the experiment, in order to be able to update the prior for any outcome.
Based on our conversation, I decided to make a small implementation of this simulation in Excel. You can download the file here.
You’ll notice that I calculate the likelihood using a binomial distribution with parameter n equal to 1. That is identical to a Bernoulli distribution, which Excel lacks for some reason. Also, I couldn’t use the same formula as in the MATLAB code, since I discovered that Excel has problems with expressions containing 0^0 too. I’m not a big expert in Excel and I’m sure there’s a more elegant way to do this, but let me know if you are able to follow what’s going on. Feel free to ask me if something isn’t entirely clear. I hope this will help you adapt your own Excel simulation.
Also, in case you’re familiar with Python, I recreated the simulation in that language too. You can download it here.
Thank for your files my approach is quite different and probably wrong because I am not really narrowing my converging to 0,03, the best would be you have a look at my approach:
[broken link]
You’re a performing one flip and then with bayes approach you’re narrowing this to a perfect distribution around 0.3 I think that thanks to the power of the binomial distribution which you’re exploiting. My approach is that without assuming that coins behave in a binomial way I just perform series of experiments and observe the outcomes, calculate new probabilities apply Bayes and move forward etc …-> the problem is that I am not narrowing very much the results around the 0.3 bias which I should… I am floating some where between 0.2 and 0.4 (may be more experiments are needed) as you can see I simulate hundreds of flips you only one…
Imre, the link is broken.
But look, if you’re calculating proportions, then the approach I described in this post will not be directly applicable. Like I said earlier, if you have a binomial likelihood, the math becomes somewhat more complicated. In my case, I only use a binomial distribution in the Excel file because there is no Bernoulli distribution. But since the the sample size parameter (n) is fixed to 1, it reduces to a Bernoulli distribution anyway.
I will be introducing the binomial distribution in one of my next 3-4 posts. And a few posts after that I will introduce the concept of conjugate prior distributions (it’s too much material to cover in a few comments). Those will help in generalizing the use of Bayes’ theorem for estimating parameters of more complicated distributions.
By the way, were you able to follow the formulas in my Excel file?
Yes no problem with your excel, we start to have a long discussion here (which may be is not the proper place) but still it’s very interesting. The link was probably waiting too long for download.
What is great with Bayes (I don’t know if I will express my self clearly) is that even if the experiments are independent the Bayes approach “seems” to keep a memory of previous state. At the end the 500 coin flip “knows” that it is “baised” even in reality the 500 coin toss should feel the same that first:-)
Yes, that is one of the great things about Bayesian approaches indeed. If the mathematics is rigorous, the prior distribution holds information about all past observed data that relates to a specific hypothesis. To quote Dennis Lindley:
Thanks for being active in this discussion. I’m sure many other readers will benefit from it.
Can you please help me understand how to get the answer of the following question?
NASA has planned five space launches with the probability of a successful launch estimated at 0.9. Assuming that all launches are independent. Calculate the mean and variance of the number of successful launches.
Thanks and i appreciate your assistance on this matter.
Hi, Charles.
This question is essentially testing your knowledge of the binomial distribution. More specifically, about calculating its mean and variance. Are you familiar with probability distributions? If not, please take a look at my post about them. Another useful post is the one about calculating the mean and variance of probability distributions. And if you like to learn more about the binomial distirbution itself, check out my post on discrete probability distrubtions You will find an introduction to the binomial distribution in the section on distrbution with finite sample spaces.
If you’re still unsure how to answer this question, please let me know which steps in particular you’re struggling with.
Hi, it is explained for one coin which can be learned by flipping many times to get bias but what if we can only flip the coin only one time? How would we measure the bias in that case?
Hi Wal,
From the clarification you gave me in personal correspondence, I understand that the problem is the following. You have a very large number of coins, each with an unknown “heads” bias P(H). You pick a coin at random and you’re allowed to flip it only once but before flipping it you’re allowed to examine the coin physically and predict its bias. And you’re looking for a way to measure the accuracy of you physically examining the coin, without necessarily using a Bayesian approach.
If you have a single coin which you’re allowed to flip multiple times, then the evaluation of the estimate is rather straightforward. Say you examined the coin physically and estimated P(H) to be 0.65. Then you decide to flip the coin 10000 times and expect about 6500 of the flips to be “heads” and 3500 to be “tails”. And if you actually get, say, 6348 “heads” and 3652 “tails”, this is pretty close to your prediction.
Now what if, instead of having a single coin with unknown P(H) that you flip 10000 times, you have 10000 different coins (each with potentially different P(H)) and you’re allowed to flip each coin only once? Well, the idea is pretty much the same. After physically examining coin 1, you estimate its bias to be, say, 0.37. This means that the expected value of flipping this coin is 0.37 heads and 0.67 tails. Then you examine the second coin and estimate its P(H)=0.43 and P(T)=0.57, which means that the expected number of “heads” in the two flips is 0.37 + 0.43 = 0.8 and the expected number of “tails” is 0.67 + 0.57 = 1.24. After estimating P(H) for all 10000 coins, you add all the P(H)’s to get the total expected number of “heads” after flipping every coin. And note that because P(T) = 1 – P(H), the expected number of heads and tails will add up to 10000 again. So, let’s say that after physically examining all 10000 coins, you expect to get 4921 “heads” and 5079 “tails”.
Finally, you actually flip the coins and count the number of “heads” and “tails”. The closer these are to the predicted 4921 and 5079, the better your predictions were.
Bottom line is that flipping the same coin multiple times is conceptually equivalent to flipping different coins once each, as long as the coins all have the same bias. And if the coins have different biases, flipping them once is conceptually equivalent to flipping a single coin multiple times which magically changes its bias after every flip. In all cases, the expected number of “heads” outcomes is determined by adding the expected values of the individual flips.
Check out my post on expected value for more intuition about this concept. And let me know if this answers your question.
is there a closed-form solution? That is, given 38 flips and 26 heads, what is the bias? Does the order of the events affect the outcome?
I may be missing something here, but, if I flip a coin 15,000 times, and I get X heads, then the “bias” of the coin is, simply, X/15,000 (the “frequentist” interpretation of probability). Why do I need to contemplate any alternative biases? Yes, if I try an alternative bias of, say, .3, the probability of getting X heads that is any distance from Z/15,000 will essentially be zero.
Here is a simpler problem. Suppose I flip a coin 9 times and I get 9 heads. Does Baye’s theorem help me compute the probability of getting a heads on the 10th flip? The coin here is clearly biased. I could start with a set of priors, say P(H) = ,1. ,2, ,3 ,,, up to P(H)=1. With each coin flip coming up heads, the post probability would get ever closer to 1. What does that tell me beyond what the simple frequentist hypothesis would say, P(H)=1. If the 10th toss is heads, then the P(H) = 9/10. What am I missing?