
What is statistics about?
Well, imagine you obtained some data from a particular collection of things. It could be the heights of individuals within a group of people, the weights of cats in a clowder, the number of petals in a bouquet of flowers, and so on.
Such collections are called samples and you can use the obtained data in two ways. The most straightforward thing you can do is give a detailed description of the sample. For example, you can calculate some of its useful properties:
- The average of the sample
- The spread of the sample (how much individual data points differ from each other), also known as its variance
- The number or percentage of individuals who score above or below some constant (for example, the number of people whose height is above 180 cm)
- Etc.
You only use these quantities to summarize the sample. And the discipline that deals with such calculations is descriptive statistics.
But what if you wanted to learn something more general than just the properties of the sample? What if you wanted to find a pattern that doesn’t just hold for this particular sample, but also for the population from which you took the sample? The branch of statistics that deals with such generalizations is inferential statistics and is the main focus of this post.
The two general “philosophies” in inferential statistics are frequentist inference and Bayesian inference. I’m going to highlight the main differences between them — in the types of questions they formulate, as well as in the way they go about answering them.
But first, let’s start with a brief introduction to inferential statistics.
Table of Contents
Inferential statistics
Say you wanted to find the average height difference between all adult men and women in the world. Your first idea is to simply measure it directly. The current world population is about 7.13 billion, of which 4.3 billion are adults. Would you measure the individual heights of 4.3 billion people? I didn’t think so. It’s impractical, to say the least.
A more realistic plan is to settle with an estimate of the real difference. So, you collect samples of adult men and women from different subpopulations across the world and try to infer the average height of all men and all women from them.
And this is how the term inferential statistics gets its name. You have a population which is too large to study fully, so you use statistical techniques to estimate its properties from samples taken from that population.
If you want a little more background on the distinction between samples and populations, please read this section of my post related to probability distributions.
The interocular traumatic test
In special cases, you might simply want to know whether a pattern or a difference exists at all. You don’t have to care about the specifics like the exact magnitude of a difference between two groups. In those cases, the simplest inference technique you can use is sometimes jokingly called the interocular traumatic test (IOTT). You apply this test when the pattern is so obvious that it hits you right between your eyes!
For example, if you’re comparing the annual salary differences between company CEOs and company janitors, you won’t need to be that skilled in statistics to conclude that there is a big gap between the two.
As you can imagine, the IOTT has very limited applicability in the real world. Many differences are much too subtle to detect in such direct ways. Not to mention that most interesting patterns aren’t answerable by simple “yes/no” questions. People have developed many statistical techniques to deal with these complex cases.
The 3 goals of inferential statistics
In inferential statistics, we try to infer something about a population from data coming from a sample taken from it. But what exactly is it that we’re trying to infer?
All methods in inferential statistics aim to achieve one of the following 3 goals.
Parameter estimation
In the context of probability distributions, a parameter is some (often unknown) constant that determines the properties of the distribution.
For example, the parameters of a normal distribution are its mean and its standard deviation. The mean determines the value around which the “bell curve” is centered and the standard deviation determines its width. So, if you know that the data has a normal distribution, parameter estimation would amount to trying to learn the true values of its mean and standard deviation.
Data prediction
For this goal, you usually need to already have estimated certain parameters. Then you use them to predict future data.
For example, after measuring the heights of females in a sample, you can estimate the mean and standard deviation of the distribution for all adult females. Then you can use these values to predict the probability of a randomly chosen female to have a height within a certain range of values.
Assume that the mean you estimated is around 160 cm. Also assume that you estimated the standard deviation to be around 8 cm. Then, if you randomly pick an adult female from the population, you can expect her to have a height within the range of 152 – 168 cm (3 standard deviations from the mean). Heights that deviate more from the mean (e.g., 146 cm, 188 cm, or 193 cm) are increasingly less likely.
Model comparison
I am briefly mentioning this goal without going into details because it is a somewhat more advanced topic which I will cover in others posts (for starters, check out my post on Bayesian belief networks — a method for belief propagation that naturally allows model comparison).
In short, model comparison is the process of selecting a statistical model from 2 or more models, which best explains the observed data. A model is basically a set of postulates about the process that generates the data. For example, a model can postulate that the height of an adult is determined by factors like:
- Biological sex
- Genes
- Nutrition
- Physical exercise
A statistical model would postulate a specific relationship between these factors and the data to be explained. For example, that genetic components influence height more than physical exercise.
Two models may postulate different strengths with which each factor influences the data, a particular interaction between the factors, and so on. Then, the model that can accommodate the observed data best would be considered most accurate.
Frequentist and Bayesian statistics — the comparison
The differences between the two frameworks come from the way the concept of probability itself is interpreted.
Overview of frequentist and Bayesian definitions of probability
In an earlier post, I introduced the 4 main definitions of probability:
- Long-term frequencies
- Physical tendencies/propensities
- Degrees of belief
- Degrees of logical support
Frequentist inference is based on the first definition, whereas Bayesian inference is rooted in definitions 3 and 4.
In short, according to the frequentist definition of probability, only repeatable random events (like the result of flipping a coin) have probabilities. These probabilities are equal to the long-term frequency of occurrence of the events in question.
Frequentists don’t attach probabilities to hypotheses or to any fixed but unknown values in general. This is a very important point that you should carefully examine. Ignoring it often leads to misinterpretations of frequentist analyses.
In contrast, Bayesians view probabilities as a more general concept. As a Bayesian, you can use probabilities to represent the uncertainty in any event or hypothesis. Here, it’s perfectly acceptable to assign probabilities to non-repeatable events, such as Hillary Clinton winning the US presidential race in 2016. Orthodox frequentists would claim that such probabilities don’t make sense because the event is not repeatable. That is, you can’t run the election cycle an infinite number of times and calculate the proportion of them that Hillary Clinton won.
For more background on the different definitions of probability, I encourage you to read the post I linked above.
Parameter estimation and data prediction
For more background on this section, check out my introductory post on probability distributions.
Consider the following example. We want to estimate the average height of adult females. First, we assume that height has a normal distribution. Second, we assume that the standard deviation is available and we don’t need to estimate it. Therefore, the only thing we need to estimate is the mean of the distribution.
The frequentist way
How would a frequentist approach this problem? Well, they would reason as follows:
I don’t know what the mean female height is. However, I know that its value is fixed (not a random one). Therefore, I cannot assign probabilities to the mean being equal to a certain value, or being less/greater than some other value. The most I can do is collect data from a sample of the population and estimate its mean as the value which is most consistent with the data.
The value mentioned in the end is known as the maximum likelihood estimate. It depends on the distribution of the data and I won’t go into details on its calculation. However, for normally distributed data, it’s quite straightforward: the maximum likelihood estimate of the population mean is equal to the sample mean.
The Bayesian way
A Bayesian, on the other hand, would reason differently:
I agree that the mean is a fixed and unknown value, but I see no problem in representing the uncertainty probabilistically. I will do so by defining a probability distribution over the possible values of the mean and use sample data to update this distribution.
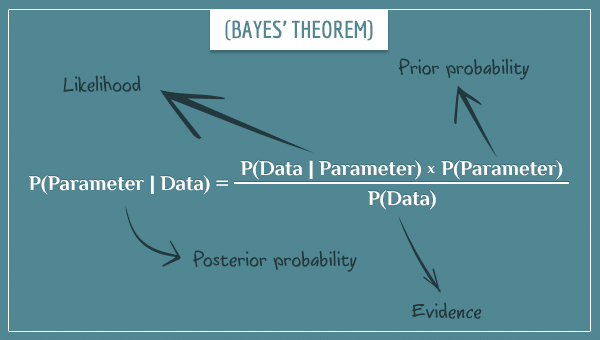
In a Bayesian setting, the newly collected data makes the probability distribution over the parameter narrower. More specifically, narrower around the parameter’s true (unknown) value. You do the updating process by applying Bayes’ theorem:
The way to update the entire probability distribution is by applying Bayes’ theorem to each possible value of the parameter.
If you aren’t familiar with Bayes’ theorem, take a look at my introductory post, as well as this post. They will give you some intuition about the theorem and its derivation. And if you really want to see the use of Bayes’ theorem in action, this post is for you. There, I demonstrated the estimation of the bias of a coin by updating the full probability distribution after each coin flip.
Frequentists’ main objection to the Bayesian approach is the use of prior probabilities. Their criticism is that there is always a subjective element in assigning them. Paradoxically, Bayesians consider not using prior probabilities one of the biggest weaknesses of the frequentist approach.
Although this isn’t a debate you can answer one way or another with complete certainty, the truth is not somewhere in the middle. In the future, I’m going to write a post that discusses the mathematical and practical consequences of using or not using prior probabilities.
Data prediction
Here, the difference between frequentist and Bayesian approaches is analogous to their difference in parameter estimation. Again, frequentists don’t assign probabilities to possible parameter values and they use (maximum likelihood) point estimates of unknown parameters to predict new data points.
Bayesians, on the other hand, have a full posterior distribution over the possible parameter values which allows them to take into account the uncertainty in the estimate by integrating the full posterior distribution, instead of basing the prediction just on the most likely value.
P-values and confidence intervals
Frequentists don’t treat the uncertainty in the true parameter value probabilistically. However, that doesn’t magically eliminate uncertainty. The maximum likelihood estimate could still be wrong and, in fact, most of the time it is wrong! When you assume that a particular estimate is the correct one, but in reality it isn’t, you will make an error. Consequently, this has lead to the development of two mathematical techniques for quantifying and limiting long-term error rates:
- null hypothesis significance testing (NHST) and the related concept of p-values
- confidence intervals
The general idea is to make an estimate, then assume something about the estimate only under certain conditions. You choose these conditions in a way that limits the long-term error rate by some number (usually 5% or lower).
I discussed the types of error rates NHST controls (as well as the correct interpretation of p-values) in a previous post about this topic. But I strongly encourage you to read that post if you’re not familiar with p-values. In fact, I encourage you to read it even if you are, due to their very frequent misinterpretation.
Confidence intervals
Confidence intervals are the frequentist way of doing parameter estimation that is more than a point estimate. The technical details behind constructing confidence intervals are beyond the scope of this post, but I’m going to give the general intuition.
Put yourself in the shoes of a person who’s trying to estimate some mean value (the average height in a population, the average IQ difference between two groups, and so on). As usual, you start by collecting sample data from the population. Now, the next step is the magic that I’m not telling you about. It’s a standard procedure for calculating an interval of values.
You determine the whole procedure, including the sample size, before collecting any data. And you choose the procedure with the following goal in mind.
- If you, hypothetically, repeat the procedure a large number of times, the confidence interval should contain the true mean with a certain probability.
In statistics, commonly used ones are the 95% and the 99% confidence intervals.
If you choose a population with a fixed mean, collect sample data, and finally calculate the 95% confidence interval, 95% of the time the interval you calculated will cover the true mean.
Once you’ve calculated a confidence interval, it’s incorrect to say that it covers the true mean with a probability of 95% (this is a common misinterpretation). You can only say, in advance, that in the long-run, 95% of the confidence intervals you’ve generated by following the same procedure will cover the true mean.
A graphical illustration of calculating confidence intervals
Click on the image below to start a short animation that illustrates the procedure I described above:

Somewhere on the real number line, we have a hypothetical mean (abbreviated with the letter ‘m’) . We generate 20 consecutive 95% confidence intervals. Two of them happen to miss the mean, and 18 happen to cover it. That gives 18/20 = 90%.
Why did only 90% of the confidence intervals cover the mean, and not 95%? The answer, of course, is that the process is inherently probabilistic and there is no guarantee that, of any fixed number of confidence intervals, exactly 95% will cover the true mean. However, as the number of generated intervals increases, the percentage that cover the mean will get closer and closer to 95%.
By the way, notice how individual confidence intervals don’t have the same width and they are all centered around different values.
Summary
In this post, I introduced the distinction between descriptive and inferential statistics and explained the 3 goals of the latter:
- Parameter estimation
- Data prediction
- Model comparison
I ignored the last goal and mostly focused on the first.
I showed that the difference between frequentist and Bayesian approaches has its roots in the different ways the two define the concept of probability. Frequentist statistics only treats random events probabilistically and doesn’t quantify the uncertainty in fixed but unknown values (such as the uncertainty in the true values of parameters). Bayesian statistics, on the other hand, defines probability distributions over possible values of a parameter which can then be used for other purposes.
Finally, I showed that, in the absence of probabilistic treatment of parameters, frequentists handle uncertainty by limiting the long-term error rates, either by comparing the estimated parameter against a null value (NHST), or by calculating confidence intervals.

As noted in previous posts as well, only referring to long-run error rates is fallacious representation of both the founders and the modern proponents of what can be broadly called frequentist inference. Regardless, I expected more of a battle in this post, given the title graphic, but the Bayesian inference was mostly missing from the text…
Looking forward to this: “In the future, I’m going to write a post that discusses the mathematical and practical consequences of using or not using prior probabilities.”
Yeah, I didn’t really go into a simulated debate between the two frameworks, despite what might be suggested by the featured image. I mostly wanted to outline the differences, without expressing any preferences.
In future posts, however… 🙂
“Confidence intervals are the frequentist way of doing parameter estimation…”
Thats actually the bayesian approach or am i wrong?
In the Bayesian framework some people use the so-called ‘credibility intervals’. They sound very similar to ‘confidence intervals’ but are actually mathematically very different.
You may also come across them under the name ‘highest density intervals’.
With the Bayesian credibility intervals you can actually make the statement “the probability that the true value of the parameter is within these boundaries”, of course subject to certain assumptions. This is not possible with Frequentist confidence intervals (in fact, it’s a common misinterpretation).
Can you help me understand this part of the post
“Bayesian, on the other hand, have a full posterior distribution over the possible parameter values which allows them to take into account the uncertainty in the estimate by integrating the full posterior distribution, instead of basing the prediction just on the most likely value”
Hi, Esha. This is a tricky topic and when I first encountered it it took me some time to get my head around it as well.
This basically boils down to Frequentists refusing to assign probabilities to parameters with unknown but fixed values (take a look at the Parameter estimation and data prediction section above to see what I’m talking about). Whereas Bayesians, having no (philosophical) problems assigning such probabilities, can obtain an entire probability distribution over the possible parameter values.
Say you’re playing a game in which you draw a coin from a bag full of coins, all with a random bias towards “heads”. The bias is a number between 0 and 1 which defines the probability of flipping “heads” with the respective coin (a bias of 0.4 means there is 0.4 probability that you will flip “heads”).
You’re allowed to flip the coin 1000 times, then place a bet on either “heads” or “tails”, and flip the coin one more time. If you correctly guess the 1001st flip, you double your money, otherwise you lose it.
What you will likely do is record the results of the first 1000 flips and try to make a guess about the coin’s bias. If your estimate of the bias is greater than 0.5, you will bet in favor of “heads” (and in favor of “tails” otherwise).
The part where you are estimating the bias is called parameter estimation. Bayesian and Frequentist approaches to parameter estimation differ not only in terms of the specific techniques they use but, more importantly, in the end result of the estimation. Since Bayesians will have no problem assigning probabilities to the possible values of the coin’s bias, they can obtain an entire probability distribution over the possible values. And therefore, they can answer questions like “what is the probability that the coin’s bias is 0.5?”. Frequentists don’t do that. Instead, their estimate of the bias will be a single number and they will have no measure of the uncertainty around that value.
For example, the maximum likelihood estimate will be 0.4 both if you flip 4 heads out of 10 flips and if you flip 400000 heads out of a million flips. But you will obviously be much more confident in your estimate in the latter case, which will be naturally reflected in the posterior probability distribution (which will be much more tightly centered around the mean).
Frequentists can use confidence intervals to partially solve this problem. When the number of flips is higher, the range of values covered by the interval is going to be much tighter. But, within that confidence interval, you will still have no measure of ‘likelihood’ for the different values. In other words, if your confidence interval is [0.3, 0.5], every value from that interval is an equally good candidate for being the actual value of the bias. When the number of flips is low, this can make a big difference.
As I said, this is a tricky topic and I am probably not covering everything to fully answer your question. Please feel free to ask for further clarification!
Regarding the answer given to the question. A Bayesian would never give a probability that the bias of a coin is 0.5 or any other value. Bayesians would provide a probability density. From that you could calculate the probability of the bias being 0.5 +/- x. A frequentist would create a hypothesis that the bias was 0.5 and then go about “testing” the hypothesis. The way the testing would be done, the frequentist would probably claim his hypothesis was correct even if the true bias were 0.498. Or else he might just say the hypothesis is incorrect. That’s one problem with the frequentist approach.
I enjoyed this post very much. To be honest, my knowledge of statistics is limited to basic classes in college and some in grad school, and I still am learning. I never understood what the MLE was, and your explanations are clear and concise without omitting crucial details. The overall distinction between Bayesian and Frequentist approaches was clear to me as well.
Thank you, and I look forward to reading more.
Thanks, Samantha, I’m glad you found the post interesting!
Up above, I see the following comment:
“Assume that the mean you estimated is around 160 cm. Also assume that you estimated the standard deviation to be around 8 cm. Then, if you randomly pick an adult female from the population, you can expect her to have a height within the range of 152 – 168 cm (3 standard deviations from the mean).
Can you explain how the range of 152 – 168 cm is 3 standard deviations from the mean?
Hi, Daniel.
I’m assuming you’re referring to the property of normal distributions of having ~99% of the probability mass within 3 standard deviations from the mean. I wasn’t really referring to that, but making the point that generally most values are “close” to the mean in terms of standard deviations. As you noticed, in my example 152-168 is only 1 standard deviation (which, if the data were normally distributed, would mean ~70% of the probability mass).
Thank you for your observation. Normal distributions are very important and I’ll most likely dedicate an entire post to them where I’ll also discuss the 68-95-99.7 rule you are referring to.
Hi. Thank you for this post. I have a question about this part:
” Once you’ve calculated a confidence interval, it’s incorrect to say that it covers the true mean with a probability of 95% (this is a common misinterpretation). You can only say in advance that, in the long-run, 95% of the confidence intervals you’ve generated by following the same procedure will cover the true mean. ”
I don’t understand why you can’t say that the confidence interval covers the mean with a probability of 95%.
Since our confidence intervals work 95% of the time, as mentioned in the second sentence, then for this particular time the probability of our confidence interval to work is 95%, which means that we get the mean with a probability of 95%.
Thank you.
Joseph
Hi Joseph, very good question. In fact, it’s a question that almost anybody who chooses to dig deep enough into Frequentist concepts encounters sooner or later.
I know what I wrote sounds counter-intuitive. It used to be counter-intuitive for me for a long time. But stay with me and I promise, once it clicks, you will have a small feeling of just been taken outside of the Matrix.
“For this particular time the probability of our confidence interval to work is 95%, which means that we get the mean with a probability of 95%.”
Let’s assume your statement is true. The first problem is something I already pointed to earlier in the post. Namely, in Frequenist statistics you don’t assign probabilities to fixed but unknown values. Granted, this is a philosophical, not mathematical problem, but this view is at the root of the Frequentist approach and was passionately defended by founders like Fisher, Pearson, and Neyman.
But okay, you can say you don’t have the same philosophical reservations and want to treat the mean like a random variable. Can you then say the probability of the true mean being within your just-calculated confidence interval is 95%? The answer is still no, and this time the problem is also mathematical.
But even without mathematics, it’s rather easy to show why. Say you have a sample of 20 students (out of 1000 students in a particular school) and you measure their height. You calculate the mean and the standard deviation and calculate the 95% confidence interval, which happens to be [160, 180] (in cm). Then you conclude that there’s a 95% probability the real mean of *all* students is between 160 cm and 180 cm. Good.
Then you draw another random sample of 20 students from the same school and calculate a confidence interval of [165, 178]. Then you draw a third sample and this time you calculate a confidence interval of [150, 167] (just happened to pick really short people).
Clearly, you can’t say that there’s a 95% probability that each of those confidence intervals will hold the true mean, as that would be a contradiction. And none of them is any more special than the rest, so you have no basis to choose any and assume the true mean is within it with 95% probability.
Does that make sense?
For more intuition, check out my post about p-values (and more specifically, the section P<0.05. So what?), where I also talk about the second most common misinterpretation in Frequentist statistics. Namely, “if p<0.05, does that mean the probability the null hypothesis is true is less than 5%?".
The post is informative and has piqued my interest to understand Bayesian analysis. I wanted to know when we report effect sizes based and confidence intervals on full model-averaged parameter estimates, does it fall in the frequentist-based approach?
Thank you, Harshad. I’m glad you find the post informative. And I’m even happier that it sparked an interest in Bayesian analysis!
Confidence intervals do come from the domain of frequentist statistics. However, effect sizes themselves are sort of framework agnostic when it comes to the Bayesian vs. frequentist analysis issue. By that I mean that you can certainly use them in both frameworks, but in a different manner. They are simply unitless measures of the size of a particular difference.
Once you have them, you can treat effect sizes themselves as random variables and do a Bayesian estimate of them. Or you can construct confidence intervals around them and then be in the domain of frequentist statistics.
Does my answer make sense? And, more importantly, did I understand your question correctly? If not, please provide a bit more details.
Thanks again for your interest!
is it possible to compare between classical and bayesian methods to estimate distribution parameters ?
what are the conditions??
Sure, Salah. The parameters I was talking about in the main text are exactly distribution parameters. Like the mean and variance/standard deviation of a normal distribution. I’m not sure what you mean by conditions.
Do you have a more specific question I can help you with?
Wonderful blog! I hope you still keep an eye on the replies. I’m in a mental deadlock on this statement from your post (I know you quote the Fisherian school correctly here):
“Once you’ve calculated a confidence interval, it’s incorrect to say that it covers the true mean with a probability of 95% (this is a common misinterpretation). You can only say in advance that, in the long-run, 95% of the confidence intervals you’ve generated by following the same procedure will cover the true mean.”
Now my intuitive response would be that this is not meaningful. I imagine having a jar of five red marbles and ninety-five black ones, a hundred in total. Blindfolded, I stick my hand in the jar and grab a random marble. Now, without opening my fist or taking off my blindfold, I guess what chance I have of having a black marble (the true mean) inside my closed fist (the confidence limits). The chance is 95%.
Now, either this is a false analogy, and I fail to see why, or it is a true analogy, and Fisherians are quibbling on a point of inference that I just don’t see the justification of.
So
Hi Hans, I’m glad you’re enjoying the posts!
I already answered a similar question. Please take a look at Joseph’s question above and my reply and let me know if it addresses your intuitive concerns too.
But let me try to expand on this issue a bit more here. Perhaps thinking about the 95% confidence interval in terms of frequencies (instead of probabilities) will make the whole thing easier to understand.
The process of collecting sample data and calculating the mean and a confidence interval around it guarantees that: if you repeat this process (and the whole process!) many many times, the confidence interval you’ve calculated will cover the true mean (wherever it may actually be) in 95% of those times. This is all the confidence interval promises. It makes no claims regarding the probability of any specific confidence interval covering the mean. Remember, the actual mean is some fixed but unknown value (and not a random variable!). In this context, probability is simply used to measure our uncertainty about where the actual mean is. But Frequentists aren’t big fans of thinking about probabilities in this manner.
In other words, if you repeat all the steps in an identical manner a very large number of times (including collecting new data each time), in 95% of those cases you will manage to capture the true mean with your confidence interval, but you’ll still have no idea which of all the many confidence intervals you’ve calculated have the mean and which don’t. Each of them is an equally good candidate. But each of them have different upper and lower bounds, so if you try to make the claim that each of those intervals has a 95% probability of covering the true mean, that would be a contradiction, yes?
Let me also try a slightly more mathematical argument.
Let’s say you’ve collected a bunch of data points X_s = [X1, X2, …, XN] (here X_s stands for a sample from a population of X). Each Xk stands for a real number like 15.23. Let’s say you calculate the mean of all numbers and a 95% confidence interval around the mean and you get:
Now let’s investigate the following claim:
“There is a 95% probability that the real (population) mean of X is within the interval [15, 25].”
In fact, let’s take a step back and investigate the claim on its own, ignoring the sample data we collected or the confidence interval we calculated. How would you go about calculating this probability in the general case?
Let’s say that, before you even collected the sample data above, you might already have some domain knowledge about X. Which, probabilistically speaking, translates to you having a prior distribution over the possible values of the mean of X. Let’s say the prior distribution is a normal distribution with a mean of 17 and a standard deviation of 4.
Now let’s use this prior distribution to calculate the probability that the mean is between 15 and 25. What you would do in this situation is basically calculate the definite integral over the said normal distribution, where the lower bound of the integral is 15 and the upper bound is 25. Are you with me so far?
Okay, now let’s take another step and look at the collected sample data. Now that we have new data, we want to calculate the posterior probability:
Applying Bayes’ theorem, the above expression is equal to:
But, think about it. Isn’t this posterior probability essentially the answer to the initial claim we started with? It calculates exactly the probability that the mean is between those two values, given the data we have (the evidence). Because this data is all we used to calculate the 95% confidence interval as well.
If we assume the confidence interval was giving this probability, then we should expect that posterior probability to be equal to 95%, yes? But in fact, if you actually calculate the posterior probability with Bayes’ theorem, it most likely be a different value. In fact, it could easily be a probability much lower than 95%! Why? Well, for one, notice that the prior distribution you start with is a strong factor in this calculation.
Thank you for replying, great! Sorry for mssing the earlier question that looked like the one I had. I’ll chew on this for a while now. I feel new questions forming already, though. 🙂
I suppose I’ll keep struggling with this concept for some time. I accept that you are right, without me really seeing why yet.
But this leads me to my main concern: What is then the use of CIs as a tool to understanding your data? It is abstract, mathematical, counter-intuitive etc. How does it help anyone make a decision? One scientist told me with a straight face that a p-value from a single study is meaningless. Well, all studies are single studies. Saying «CI95%s have a high chance of containing the true mean, but only if you have an unlimited number of them» does not help you in any real sense of the word.
All of this is important for inference, evidence, decision making which Is my real point of interest.
Hi again!
I have a couple of thoughts on your examples:
1. The «can’t all be true at the same time» does not convince me that catching the true mean inside your CI limits is not a stochastic process. Consider a jar with only two marbles, one red and one black. You grab one marble with each hand. What is the chance that the marble is in your left hand? It is 0.5 although you don’t have a clue which hand is the better candidate and they can’t both be holding the red marble at the same time.
2. In your mathematical example you show that calculating the probability of finding the true mean has different results when you take the data distribution into account compared with not using the distribution. But I don’t see how this matters, or why it would show that the CI95% is not likely to contain the true mean.
Hi again, Hans!
Well, here you have basically touched upon some common points of criticism towards frequentist statistics. Indeed, frequentists historically strongly resisted the intuitive temptation to assign probabilities to hypotheses. And to any non-repeatable event in general. If you asked them about the probability of the true mean being within a particular interval, they would respond that this is a meaningless question, as that particular mean is some fixed but unknown value, not a random variable (hence, you can’t assign probabilities to it).
The reason that scientist told you that a p-value from a single study is meaningless is probably because he was implicitly making the same argument. The p-value by itself doesn’t tell you anything about the probability of your study’s hypothesis being true. Its only role is to be a sort of criterion for whether to reject or not reject your null hypothesis. And, frequentists argue, if all studies followed this procedure, in the long run you will be mostly accurate about the null hypotheses you’ve rejected (only 5% of them will actually have been “true”, if you’re using p=0.05).
Is this good enough? Well, empirically this has been a matter of different taste (and historically, a matter of heated debates!). Your comment suggests that you’re not fully satisfied with it, as you also seem to be seeking a way to assign a number to the uncertainty of a particular hypothesis being true or false. And I would personally agree with you, as I am also interested in those kinds of questions.
Of course, that doesn’t suggest that the frequentist approach isn’t valuable in its own way. But it’s important to remember the philosophical and mathematical framework underlying it, in order to make the proper inferences based on frequentist analyses.
Okay, let me try to adapt your marble example to confidence intervals. Imagine you’re working in a shopping mall and you decide to play the following game.
Every time a new person between ages 20 and 30 enters the mall, you measure their height. When you have measured 100 heights, you calculate the sample mean and variance and construct a 95% confidence interval. Then you write down the boundaries of the interval, put the paper inside the marble, and throw the marble in a jar. Then you reset your counts and the next person to enter becomes the first in your next sample and you repeat this process many times and have a new marble for each sample of 100 consecutive people. Say you play this game for a full year and manage to collect 1 million marbles, each containing a confidence interval.
For the sake of this example, let’s assume that only residents of that city ever enter the mall and each citizen aged 20-30 has the same typical frequency of visiting the mall at any given day/time of the year. Also, let’s assume that the height distribution of your citizens isn’t anything untypical.
It is true that roughly 95% of the marbles in the jar will have confidence intervals containing the true mean of the population of 20-30 year-old citizens (if you were to actually measure it).
Now, let’s say you pick a marble from the jar at random. Before you open the marble and see the confidence interval values, I ask you: “what is the probability that what’s written on the paper will contain the true mean height”?
You would then reply: “Well, the probability is 95%, because 95% of the marbles contain the true mean. And I picked a marble at random, so there’s a 95% chance I’m holding a marble with the true mean in my hand.”
“Fair enough. Now let’s go ahead and open the marble.”
You open it and you see that it holds the confidence interval [195, 205]. Now my question to you is “What is the probability that the mean height of all 20-30 year-old citizens is a value between 195 cm and 205 cm?”
Think about it. Would your answer still be “95%”? And if yes, my follow-up question to you would be “How much money would you be willing to bet, and at what odds, that if you actually measured the true mean height it will be between 195 and 205?”
You see, now that you’ve seen the actual CI values, you have some new information to take into account. Wouldn’t it be much more probable that there was something unusual about this sample, rather than that it’s a typical sample? For example, maybe there was a basketball tournament in the city that day and the players of all teams decided to go to the mall together after the tournament. That’s why you got a sample of 100 people that was dominated by really tall people and you got an unusual confidence interval for that marble.
Surely, you got very unlucky in picking exactly that marble, since most marbles’ boundaries will look like much more reasonable candidates for containing the true mean. But since it’s a stochastic process, some of your CI will be like that.
The key thing to understand here is that the following 2 questions are different and don’t have the same answer (far from it!):
Question 1: “What is the probability that a randomly picked marble will contain the true mean?”
Question 2: “What is the probability that a randomly picked marble that happened to represent the confidence interval [195, 205] contains the true mean?”
The first one is about a repeatable process. Namely, randomly picking a marble, reading its CI, and checking if it contains the true mean.
The second one is about a hypothesis. Namely, the hypothesis that the true mean is between 195 and 205. Sure, those values came from a jar containing marbles of which 95% have CIs with the true mean. But that’s not the full story. When you’re dealing with actual values, you have other sources of information to consider in calculating the actual probability.
By the way, if you’re familiar with the Monty Hall problem, the intuition there is somewhat similar. Once one of the 3 doors has been opened by the host, if you randomly pick one of the remaining 2 doors, you will get the car with a 50% probability. But, if you take into account the extra information coming from the host, you can do better and increase your chances of finding the car to ~67%.
Hi, Ctaeh!
Thank you so much for taking the time to replying at such length! Also grateful for the personal notification that you had posted a reply for me.
To the first part, you are right that I feel something is missing to the frequentist picture of things. I’ve had a few discussions with a scientist who’s a diehard Popperian/Fisherian/frequentist. His views seem waterproof, but somehow unproductive. Can’t say exactly why and how yet, I’m just getting my teeth into the stuff.
As for the marble example, I do agree that the view on what’s in the CI could change when you can assess the content. But my in my mind the framework of the thought experiment was that our data analysis yields fists, not marbles. So the CI would hold something we can’t check out further. Let’s imagine the CI holds data from a planet we have no additional information on. If one was forced to gamble onthe CI, taking the bet at odds of 95 to 5 and up is then a win in the long run.
The Monty Hall problem analogy here would be to open one hand and see if the red marble is there, and then change your mind about the probabilities concerning the other fist.
Fun if you have the time for some thoughts, but you’ve been more than kind already.
Cheers, Hans
It’s not so much about the ability to collect further data or not. It’s about the fact that, when you’re considering the probability of a specific hypothesis being true (namely, the probability of the mean being within a particular interval), you need to consider the prior distribution of the hypothesis (this comes directly from Bayes’ theorem). If you don’t, then you’re not calculating probabilities but something else.
Even if you’re collecting data on the planet Earth, you can still win in the long-run if you bet with 95:5 odds that each CI you’ve constructed following the same procedure will hold the true mean. Notice that there is no mention of any specific values for the boundaries of the CI. You just know that 95% of the CIs will contain the true mean.
But if you have actual values for the boundary of the interval, then whether the mean is within that interval or not becomes a different independent question, unrelated to the CI you just calculated.
Here’s another way to demonstrate this to you. Let’s say you calculated some CI for the mean height of a population and you came up with the interval (in cm) [163, 181]. You have a friend who’s also interested in the mean height of the same population and you tell them:
“There’s a 95% probability that the mean of the population is between 163 cm and 181 cm.”
“How come?”
“Well, I just collected 100 people’s heights and constructed a 95% confidence interval. The interval I got was [163, 181].
“Oh yeah? Well I just did the same thing and I got an interval [164, 180]. So there’s also a 95% probability that the true mean is between 164 cm and 180 cm.”
A third friend (also interested in the question) overhears your conversation and joins in:
“Whoa whoa, guys. Actually, just an hour ago I did the same thing you did and got a confidence interval of [158, 185]. So, there’s a 95% probability that the true mean is between 158 cm and 185 cm.”
Now, I ask you. Are all those statements mutually consistent? If you say yes, then you would be violating the axioms of probability theory. The actual answer to all questions in the form “what is the probability that the true mean is between X and Y?” should be answered by integrating the probability distribution of the true mean from X to Y (do you agree?). And then if we assume, for example, that there’s a 95% probability that the [163, 181] interval contains the true mean, then the probability of the interval [164, 180] cannot also be 95%, since the latter is a proper subset of the former (hence, its probability must be less).
Anyway, confidence intervals don’t tell us anything about the probability distribution of the mean. Nor are they intended to. In fact, frequentists will argue that even thinking about such a probability distribution is meaningless, as the true mean isn’t a random variable.
But even if we ignore that philosophical issue and construct a probability distribution for the true mean, then you would do so by collecting the same data as the one you collected for constructing the confidence interval in the first place. And as you collect more data (and update the probability distribution using Bayes’ theorem) then the more data you collect, the more the posterior will be approaching a narrower and narrower distribution around the true mean (it will be converging to a delta function, if you’re familiar with the term). And, at each moment, you can calculate the probability of the true mean being within a certain interval by integrating the posterior over that interval.
Notice, you don’t need to have some other, independent sources of information about the mean. Even if you’re collecting the data from a distant planet, you can still keep collecting the same data you used for constructing the confidence interval to update the posterior distribution. Then you can make actual probabilistic statements about the true mean being within a certain interval.
To iterate a point from my previous reply:
The important thing to realize is that the following 2 questions are very different, even though on the surface they may seem like they’re the same:
1. What is the probability that an arbitrary 95% CI will contain the true mean?
2. What is the probability that the true mean is between X and Y?
If you don’t care about knowing what the true mean is, then you can safely bet on ANY CI (without even looking at its boundaries) and you will win 95% of the time. But if you want to make probabilistic statements about a specific interval, then you need more. Even if all you have in your hand is a single CI you just calculated and you specifically want to frame the probability in terms of that CI, then you would do something like:
where:
A = The true mean is between 163 and 181
B = I just collected data from 100 people and the 95% CI I constructed happened to be [163, 181]
You see how in no way does it follow that P(A | B) should equal 0.95, right? That is, P(B | A) * P(A) / P(B) can be equal to anything, depending on the values of each of the 3 terms.
By the way, don’t worry about asking more questions. This is a tricky concept to get one’s head around and I’m sure other people would have similar questions and reading this conversation is as helpful to them. I myself have had my struggles too.
Hey, I think I got it now! You are right about that Matrix analogy! It’s dawning on me that frequentist analysis and “testing” doesn’t tell you a lot about your hypotheses. It is primarily about the data. However, that seems to be a backward and counter-intuitive type of investigation. I bet that’s why loads of people (practicing researchers too) get it wrong. We *crave* knowledge of what the data says about our hypothesis!
I guess this also means that when people try to amend significance hysteria by advising that we should just show confidence intervals, it doesn’t really help matters at all, because single CIs do not represent your data well.
Doctor, I think I may be a Bayesian!
This kind of reminds me of this famous quote by Jacob Cohen 🙂
“What’s wrong with null hypothesis significance testing? Well, among many other things, it does not tell us what we want to know, and we so much want to know what we want to know that, out of desperation, we nevertheless believe that it does!”
Like I said in an earlier reply, the important thing really is to remember the kind of philosophical and mathematical framework frequentist statistics is based in, in order to not make faulty conclusions. Frequentist statistics’ focus is on limiting long-term error rates, not on estimating probabilities of specific hypotheses. In a way, the philosophy there is “If p<0.01, just accept that the null hypothesis is false (while acknowledging that you could be wrong) and that way you will only be wrong about 1% of the nulls you've rejected. Don't get too hung up on any one particular hypothesis - if you're wrong, you will find out sooner or later."
Anyway, thanks for all the questions. I think this was a very good discussion that is going to be helpful to anybody who is having similar difficulties with interpreting results of frequentist analyses.
Hi, thank you for the article!
However, I have one question regarding this line: “However, for normally distributed data, it’s quite straightforward: the maximum likelihood estimate of the population mean is equal to the sample mean.” Wouldn’t the MLE of the population mean be the true mean, but the sample mean be dependent on which samples you have?
Best, Ola
Hi, Ola!
The maximum likelihood estimate of a parameter is not the same as the true value of the parameter. Well, it’s an estimate of the true value.
Let’s say you have a population whose mean is 20 but you don’t know it yet. Then say you take a sample from that population and calculate its mean which happens to be 22.5. At this point you say that based on this sample “the maximum likelihood estimate of the true population mean is 22.5”. So, the true mean is 20 but because you don’t know that, you can only estimate it.
The maximum likelihood estimate is basically like a guess for the true mean. There are other types of estimates of population parameters from sample data (like the maximum a posteriori estimate), which are more than just the mean of the sample. I will talk about those in future posts.
Does this clear things up for you? Let me know if you have more questions.
Hello,
Question about a comment you made:
“Frequentists don’t do that. Instead, their estimate of the bias will be a single number and they will have no measure of the uncertainty around that value.
For example, the maximum likelihood estimate will be 0.4 both if you flip 4 heads out of 10 flips and if you flip 400000 heads out of a million flips. But you will obviously be much more confident in your estimate in the latter case, which will be naturally reflected in the posterior probability distribution (which will be much more tightly centered around the mean).”
I’m finding it hard to believe that the frequentist approach doesn’t take into account the fact that the mean will be more likely near the center than the edge of the confidence interval.
Hi John,
You raise an interesting question! Is the mean really more likely to be near the center of a confidence interval than near the edges?
Well, the first thing we need to clarify here is that in the frequentist framework you don’t assign probabilities to fixed values (like the mean of a population). This means that the whole question about the probability of the mean being closer to the center or the edges of a CI is not defined under this framework. To make any probabilistic claims about the value of the mean, you need to be operating under the Bayesian framework.
But, for the sake of argument, let’s ignore this problem and try to interpret a CI in a Bayesian way. Can we then say that there is a higher probability that the mean is closer to the center than to the edges of a CI? The answer is still ‘no’.
Take another look at the section A graphical illustration of calculating confidence intervals in the main text. In the animated simulation, pay attention to the confidence intervals that cover the true mean. You see how some of them barely “catch” it (the mean is very close to the edge) while others “catch” it more towards the center? For ease of reference, let’s call the first kind CI-edge and the second CI-center.
In order for the original claim to be true, it should generally be the case that of the CIs that cover the true mean, a higher percentage will be of the CI-center type than of the CI-edge type. But the procedures followed for constructing a confidence interval make no such promise! All they’re supposed to guarantee is that 95% of the CIs will cover the true mean, no matter how (close to the center or close to the edges).
Note that there isn’t a single way of constructing confidence intervals. Even though conventions do exist, there are many procedures that would construct a confidence interval and different procedures will generally produce different confidence intervals for the same sample data. Some of them might indeed lead to a higher CI-center type CIs than others, but this is by no means a requirement that a CI generating procedure must follow.
Does this make sense? Please let me know if I managed to answer your question.
Thanks for your response. What about the normal approximation to the binomial distribution? Is that confidence interval more likely near the center?
Not necessarily.
Whether this is the case will depend on the parameter p of the binomial distribution, as well as on the sample size and the desired confidence level. For example, if your confidence level is higher (say 99%), that will make the width of the confidence interval bigger (all else being equal). And, the wider the CI is, the less likely it is that the true mean will be near the edges.
This comes from the fact that:
1) The CI is centered around the mean of the sample
2) The sample mean is an unbiased estimator of the true mean of the population
In other words, because the sample mean is an unbiased estimator of the true population mean, you can generally expect that the population mean will be closer to the sample mean (and hence, to the center of the CI).
But you can easily have a case where the true mean happens to be closer to the edges than to the center of a confidence interval. For example, if the population mean (the parameter p) is around 0.5 and you’re calculating a 70% CI based on a sample size around 50, the true mean is about as likely to be near the center of the CI as near the edges.
And even when the true mean is closer to the center of the CI more often, this can be anything from 60% of the time to close to 100% of the time. It will all depend on the factors I mentioned above (sometimes in complicated ways).
Bottom line is that confidence intervals were never intended to provide information about the question we started with. Once you have a CI, you have no reason to think that any value inside the interval is a better candidate to be the true mean compared to the others.
Frequentist statistics doesn’t care about questions related to assigning probabilities to fixed but unknown values.
Do these explanations help you in understanding my first answer to your original question? Let me know if you need clarification about any part of them.
I gotta say that this discussion gave me some new ideas on what to include in the post on confidence intervals I’m planning to write at some point. Thanks for raising this question!
Hi,
I think I am late but I just I want to encourage you to publish that follow-up entry on why the mathematics are different in the two approaches and the truth is not anywhere in the middle.
I could claim to be an expert on Statistics yet I think it is the first time I really grasp the Bayesian “flavour”.
Thanks!
Thank you, Miguel! I’m very happy that you found my post useful.
Ah, yes. That post you mention is on my (very long) list of drafts. I will surely get to it at some point! Feel free to subscribe to my mail list (on the top right) if you don’t want to periodically check for it.
Cheers
Hello, thanks for the really insightful posts! I was hoping you could help me clear up some things I’m still confused about from the frequentist perspective regarding data prediction and model comparison. Basically, I’m trying to fit everything I know about inferential statistics into one of the three categories you mention to make sure I’m understanding things correctly.
If I’ve done MLE to estimate the parameters of a distribution to fit a model to my data, and then I collect more data and I want to determine the probability that this new data comes from my fitted model, would this be considered data prediction, model comparison, or something else? Could you maybe give a more concrete example of data prediction from both the frequentist and bayesian perspectives? At the end of your post, when you talk about p-values and confidence intervals, it seems this focused just on parameter estimation, or did I misinterpret this?
Is frequentist NHST considered model comparison (could the null and alternative hypotheses be thought of as two different models), and if this not always true, could you explain why and provide an example of a frequentist approach to model comparison?
Cheers!
Hello, Jai! That’s an awesome question. I see that you’re trying to organize all these concepts in your head which means you really want to understand things in depth.
Yes, like I said in the post itself, I barely went into any details about model comparison because I’m planning to write an entire post on the topic (maybe even more than one post). But let me try to clarify things for you here.
Let’s say you somehow encounter some data. Let’s take the “female height” example I used in the post. Say you have the heights of 400 randomly picked adult females. Then you start reasoning “I’m going to assume that the distribution of all adult female heights is a normal distribution. So let me fit a normal distribution to the the data above.”
Fitting a normal distribution basically means to find the mean and standard deviation that would best fit the observed data. You do MLE and determine that the best fitting normal distribution is one with a mean of 160 cm and a standard deviation of 8 cm. So far, you’ve only done parameter estimation.
Then, after hearing you’ve done some analysis, I tell you “Hey, I have a 7 year-old daughter. What do you think is the probability that she will be tall when she grows up?”. And you ask me “What do you mean by ‘tall’?”. And I say “Hmm. Well, I consider a height of 170 cm or more to be tall for a woman.” And then you say “Okay, no problem. The height for adult women follows a normal distribution with mean=160 and std=8. Therefore, the probability of your daughter reaching a height of 170 cm or more is the integral from 170 to positive infinity over the normal distribution with those parameters. Which is around 0.11. Which means, the probability that your daughter will be a ‘tall’ woman (by your definition) is around 11%.”
What I just described is an example of data prediction. So far, so good?
But then, a friend of yours overhears our conversation and says “Wait a minute. Your initial assumption that female height has a normal distribution is probably wrong. I think that height actually has a gamma distribution. Your parameter estimation is irrelevant because you should have done it with a gamma distribution instead, not a normal distribution. So, your prediction is probably wrong too.”
Well, the process of resolving this disagreement would be an example of model comparison. You see, when you do parameter estimation, you do it in the context of some more basic assumptions. In this case, the assumption was that of the normal distribution (as opposed to other distributions). The set of all these basic assumptions is your model. An alternative model would be anything that has one or more different assumptions. In the example above, the different assumption is that the distribution is a gamma distribution with parameters shape and scale, not a normal distribution with parameters mean and variance.
Model comparison essentially means determining which model fits the data better. That is, if you take the best possible fit of each model, which one seems like a more adequate fit?
As for how model comparison differs between Bayesian and frequentist approaches… Well, this is a long topic and I won’t be able to go into the details of the different approaches here. But let me try to give you some basic intuition.
In parameter estimation, you consider how good of a candidate each possible value of the parameter is to fit the data, right? Bayesians would construct a probability distribution over the parameter space, whereas frequentists would calculate a point estimate (MLE).
Now, in model comparison, Bayesians would instead build a probability distribution over the model space. If there are only 2 candidate models, you would calculate the probability of each model, given the data, in a Bayesian way (by having some prior distribution over the models). Then there are different ways to select the best model based on those probabilities.
On the other hand, frequentists will not bother trying to assign probabilities to the different models because in this framework probabilities apply only to data, not to things like parameters or models. One naive approach to frequentist model selection would be to directly compare the MLEs of the two models. Whichever model gives the highest maximum likelihood, it is to be selected. But with that approach you would quickly hit one of the most serious problems in the field: that of overfitting. There are more sophisticated methods that frequentists would use to do model comparison, like cross-validation and likelihood-ratio test.
And yes, you can view NHST as a type of model comparison. In a typical frequentist setting, you would have one of your models (the simpler one) be the null hypothesis and the other model be the alternative hypothesis. Then you would derive some measure for the error of each model and perform a particular NHST type of analysis that tests if the alternative model’s error is lower than the “null” model’s error. If, based on the p-value, you manage to reject the null hypothesis, you select the alternative model over the “null” one. If not, you accept the “null” model.
I hope I managed to answer your question. I’m going to give a much richer explanation of these things in future posts. Feel free to subscribe to my mail list if you want to get a notification when that happens.
Cheers!
Terrific, this post and comment has made things much clearer for me! Thanks again!! Looking forward to the future posts : )
Hi The Cthaeh,
I just stumbled upon your website and I love it. The topics are interesting, and the explanations are lucid.
I hope you won’t mind my recurring to a discussion thread which I can’t quite understand, or, if I do understand it, I can’t agree with it.
Under the post “Frequentist and Bayesian Approaches in Statistics,” there is a discussion about the interpretation of confidence intervals. I take it up midstream: You say:
Here’s another way to demonstrate this to you. Let’s say you calculated some CI for the mean height of a population and you came up with the interval (in cm) [163, 181]. You have a friend who’s also interested in the mean height of the same population and you tell them:
“There’s a 95% probability that the mean of the population is between 163 cm and 181 cm.”
“How come?”
“Well, I just collected 100 people’s heights and constructed a 95% confidence interval. The interval I got was [163, 181].
“Oh yeah? Well I just did the same thing and I got an interval [162, 180]. So there’s also a 95% probability that the true mean is between 162 cm and 180 cm.”
A third friend (also interested in the question) overhears your conversation and joins in:
“Whoa whoa, guys. Actually, just an hour ago I did the same thing you did and got a confidence interval of [158, 185]. So, there’s a 95% probability that the true mean is between 158 cm and 185 cm.”
Now, I ask you. Are all those statements mutually consistent?
I would argue that there is nothing inconsistent about these results. The reason is that the true mean is unknown, and unless you do a census of the population, unknowable. Based on each sample therefore, a different underlying population is inferred, and without a census of the population, you have no basis to prefer one inferred population to another.
Thus, the following statement seems to me not valid. “And then if we assume, for example, that there’s a 95% probability that the [163, 181] interval contains the true mean, then the probability of the interval [162, 180] cannot also be 95%, since the latter is a proper subset of the former (hence, its probability must be less).” (I assume you meant to write that the second interval was [164, 180] so that it would be contained within the interval [163, 181]. But, as suggested by my argument below, even that would only imply that that the population which one would infer from second sample has a smaller variance than the population which one would infer from first sample.)
Thus, neither [162, 180] nor [164, 180] is a proper subset of [163, 181]. They are different, independent samples. The population implied by the latter sample is different than the population implied by the former sample. Since the true population is unknown, there is no basis for saying that one sample is more correct than the other or that one is a subset of the other sample. One could think of each sample as coming from a different (inferred) population; you can’t know which sample came from the (inferred) population which most closely matches the actual population, and thus you have no basis for preferring one sample to another, nor to say that the samples are inconsistent one with another.
I would interpret the samples as follows:
First sample: I do not know what the true mean is, but based on my sample, I believe, to a 95% likelihood, that it lies between 163 and 181, and my best estimate is the center of that interval, 172.
Second sample: I do not know what the true mean is, but based on my sample, I believe, to a 95% likelihood, that it lies between 162 and 180, and my best estimate is the center of that interval, 171.
Third sample: I do not know what the true mean is, but based on my sample, I believe, to a 95% likelihood, that it lies between 158 and 185, and my best estimate is the center of that interval, 171.5.
Each of the samples implies a certain underlying population; in particular, each sample implies a population which has a different mean and variance than that implied by the other samples, but since the true parameters are unknown and unknowable, there is nothing inconsistent about different samples implying different underlying populations.
Once you’ve calculated a confidence interval, it’s incorrect to say that it covers the true mean with a probability of 95% (this is a common misinterpretation). You can only say, in advance, that in the long-run, 95% of the confidence intervals you’ve generated by following the same procedure will cover the true mean.
I would argue that both statements are correct: a confidence interval covers the true mean with a probability of 95%, and in the long-run, 95% of the confidence intervals you’ve generated by following the same procedure will cover the true mean.
If you interpret each of these results as merely “You just know that 95% of the CIs will contain the true mean,” you are throwing away information which you expended resources to obtain.
I have long had an interest in these topics, although it has been dormant for some years. I look forward to a response from you in the hope that I can learn more about these things.
Kudos for a great website.
David
Hi David, thank you for your nice words about the website! Hopefully you will find it even more useful and interesting as my news posts arrive!
Let me address your questions:
“I would argue that there is nothing inconsistent about these results.”
You’re right, the results themselves are fine. It’s the probabilistic statements drawn from these results that are inconsistent with the axioms of probability theory (that is, if you try to make probabilistic statements about the unknown true mean).
“I assume you meant to write that the second interval was [164, 180] so that it would be contained within the interval [163, 181]”
Yes, good catch! I definitely meant 164 there, not 162. I edited my old comments to fix the error.
“Thus, neither [162, 180] nor [164, 180] is a proper subset of [163, 181]. They are different, independent samples. The population implied by the latter sample is different than the population implied by the former sample. Since the true population is unknown, there is no basis for saying that one sample is more correct than the other or that one is a subset of the other sample.”
You’re right, they are all different and independent samples. But they are all samples of the same population. There are no different populations here. If your point is that in my particular hypothetical example we could potentially be dealing with different populations, just imagine an even stricter scenario. Let’s say there’s a 3-hour-long concert taking place in a stadium and the audience is exactly 50000 people. Also, assume that during the entire concert nobody leaves or enters the stadium, so we know for sure that the population we’re interested in remains the same.
Now, let’s say during the concert you take several independent random samples of 100 people to measure their height and calculate a CI around the sample mean. Each time you get a different 95% interval and based on that interval you decide to make a probabilistic statement about the underlying population of 50000.
Let’s imagine an even more extreme example. One of the confidence intervals is [165, 179] and the other is [180, 188]. Notice that they’re completely non-overlapping. If, based on these two confidence intervals, we try to make the following statements about the underlying population P:
“There’s a probability of 95% that the true mean of P is between 165 and 179 cm. Also, there’s a 95% probability that the true mean of P is between 180 and 188 cm.”
Do you agree that these two statements can’t both be true for the same population?
Hi The Cthaeh,
Thanks for such a prompt reply!
I do think that both statements, “There’s a probability of 95% that the true mean of P is between 165 and 179 cm. Also, there’s a 95% probability that the true mean of P is between 180 and 188 cm.” could be true about the same population.
Saying that there is a 95% probability that the true mean of P is between 165 and 179 cm is not the same as saying that the mean is between 165 and 179. Hypothetically, the true mean could be, say, 190 cm, and it would be possible to draw samples of 100 out of 50,000 to give the results you posited.
I am trying to relate this difference in interpretation to the larger point of your original post. In so doing, I decided that I do not fully understand this paragraph:
I showed that the difference between frequentist and Bayesian approaches has its roots in the different ways the two define the concept of probability. Frequentist statistics only treats random events probabilistically and doesn’t quantify the uncertainty in fixed but unknown values (such as the uncertainty in the true values of parameters). Bayesian statistics, on the other hand, defines probability distributions over possible values of a parameter which can then be used for other purposes.
You wrote: If your point is that in my particular hypothetical example we could potentially be dealing with different populations
I think that is my point. So long as you have not done a census of the population, the true population, and thus the true mean, must be unknown and unknowable.
I will posit a wild hypothetical which might lead to a clarification. Suppose out of a population of 50,000 you take a random sample of 49,999, and based on that sample you calculate an estimate of the mean lying between 180.34 and 180.41 with a probability of 99.99999%.
Now, however, suppose that the true mean is 190. How could that be?
The obvious answer is that the last item in the population, which by chance we did not include in our sample, had a value in excess of 500,000.
Now, as mere numbers in a population, this would be entirely possible. But if you say the population was human beings and the values were heights, then you can say that the result is absurd. You would throw out the last value as an outlier.
In this case, you are using additional information beyond the sample taken. When you say that the population consists of heights of human beings, you are adding additional information about the range of the population, to wit, that a value of 500,000 cm is outside of the allowable range, and must not be taken into account.
This additional information may be the kind of information which justifies an assumed a priori probability in a Bayesian approach.
But I can’t see how this relates to the point and range estimates of the frequentist approach.
In any event, thank you for participating in a dialogue.
Regards,
David
“I do think that both statements, “There’s a probability of 95% that the true mean of P is between 165 and 179 cm. Also, there’s a 95% probability that the true mean of P is between 180 and 188 cm.” could be true about the same population.”
Well, not if you’re working with the current axiomatization of probabilities. If 95% of the probability mass is between 165 and 179, you’re only left with 5% for the rest of the sample space.
“Hypothetically, the true mean could be, say, 190 cm, and it would be possible to draw samples of 100 out of 50,000 to give the results you posited.”
Sure, that’s what I’m saying. If you draw many samples out of the same population, some of them will have very different means. But you need to be careful about the difference between making statements about a population and making statements about samples drawn from the same population.
“I am trying to relate this difference in interpretation to the larger point of your original post. In so doing, I decided that I do not fully understand this paragraph”
Oh, I see. Have you read my post where I talk about the different philosophical views/definitions of probabilities? If not, it might help clarify some things. The main point is that, in the frequentist framework, a statement like “there’s a 95% probability that the true mean is between X and Y” doesn’t even make sense. The only reason we’re having this conversation is because, for the sake of argument, we’re trying to give a Bayesian interpretation of frequentist concepts like confidence intervals. Which we’re not supposed to do in the first place!
“I will posit a wild hypothetical which might lead to a clarification. Suppose out of a population of 50,000 you take a random sample of 49,999, and based on that sample you calculate an estimate of the mean lying between 180.34 and 180.41 with a probability of 99.99999%.
Now, however, suppose that the true mean is 190. How could that be?”
Well, it can’t be. In your hypothetical, clearly there was a measurement error somewhere, right?
“Now, as mere numbers in a population, this would be entirely possible. But if you say the population was human beings and the values were heights, then you can say that the result is absurd. You would throw out the last value as an outlier.”
Not really. An outlier is still a true (but untypical) value. In your example, we’re talking about measurement errors, since 50000 cm tall people simply don’t exist.
By the way, throwing away outliers isn’t necessarily a good practice. In fact, technically it’s not right and a lot of times people do it out of convenience.
“In any event, thank you for participating in a dialogue.”
You bet, thank you for being active too! Any question/uncertainty that any reader has, chances are other readers have them too and these dialogues are potentially useful for them as well.
Cheers
Just wanted to comment to say thanks for the clear and informative article, and the care taken to engage with all comments and questions: I’m currently doing a basic course in inferential frequentist statistics at uni, and had the same question as many about what confidence intervals actually represent, and what their actual utility is if they don’t give us a ‘probability’; this post and the discussion in the comments has really helped.
I’ve read through your discussion with Hans Petter Kjæstad and I have to agree with your conclusive remark:
“I think this was a very good discussion that is going to be helpful to anybody who is having similar difficulties with interpreting results of frequentist analyses”
– this was certainly the case for me!
Thank you for the feedback, Tom! I’m glad the post and the comments have had the desired effect on you, as a reader.
A good opportunity for me to remind readers that asking questions isn’t in any way an act of selfishness (in the negative sense of the word). Most of the time it’s a win-win situation for you and for many other readers. Remember that if you ever hesitate to ask your question because you think it’s too basic 🙂
Hi THE CTHAEH,
thank you for your very well crafted post.
Pardon my ignorance: who are the two people in the photo at the beginning?
Hi Dario,
Those are Dennis Lindley (on the left) and Ronald Fisher (on the right). Lindley was a very outspoken proponent of Bayesian statistics, whereas Fisher is one of the fathers of Frequentist statistics (and he was a big opponent of Bayesian statistics during his lifetime).
As a little bit of background information, this debate was quite intense in the first half of the 20th century and my image is a humorous reference to this debate.
Glad you enjoyed the post!