The Sum Operator: Everything You Need to Know

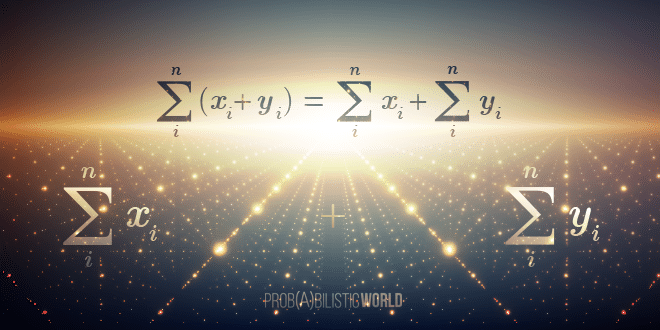
The sum operator (capital Greek letter Sigma), light beams in the background

I have used the sum operator in many of my previous posts and I’m going to use it even more in the future. I’ve introduced bits and pieces about this notation and some of its properties but this information is scattered across many posts. For these reasons, I decided to dedicate a special post to the sum operator where I show you the most important details about it.

The first time I mentioned this operator was in my post about expected value where I used it as a compact way to represent the general formula. Since then, I’ve used it in many other posts and series (like the cryptography series and the discrete probability distribution series). This is an operator that you’ll generally come across very frequently in mathematics.

So, given its importance, in today’s post I’m going to give you more details and intuition about it and show you some of its important properties. These properties come directly from the properties of arithmetic operations and allow you to simplify or otherwise manipulate expressions containing it.

In my introductory post on numbers and arithmetic I showed you some operators that represent the basic arithmetic operations. For example, the + (“plus”) operator represents the addition operation of the numbers to its left and right:

$2 + 3 = 5$

Similarly, the √ (“radical”) operator represents the root operation:

$\sqrt 4 = 2$

You can view these operators as types of instructions. For example, the + operator is instructing readers of the expression to add the numbers between which it’s written. Likewise, the √ operator instructs you to find a number whose second power is equal to the number inside it.

Well, you can view the sum operator, represented by the symbol ∑ (the Greek capital letter Sigma) in the exact same way. It has some stuff written above and below it, as well as some expression written to its right. Which, together, also represent a particular type of instruction. Let’s see what it is.

The anatomy of the sum operator

The notation surrounding the sum operator consists of four parts:

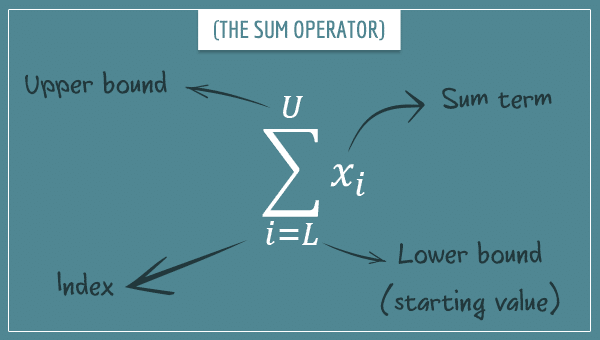
A capital letter Sigma representing the sum operator, along with its four components: the index, the lower bound, the upper bound, and the sum term (labeled with arrows)

The number written on top of ∑ is called the upper bound of the sum. Below ∑, there are two additional components: the index and the lower bound. Notice that they’re set equal to each other (you’ll see the significance of this in a bit). Finally, just to the right of ∑ there’s the sum term (note that the index also appears there). It’s important to point that U and L can only be integers (or sometimes even constrained to only be natural numbers). You’ll see why as we make progress.

I’m going to explain the role of each of these components in terms of the instruction the sum operator represents. Unlike basic arithmetic operators, the instruction here takes a few more words to describe.

You can think of the sum operator as a sort of “compressed sum” with an instruction as to how exactly to “unpack” it (or “unzip” it, if you will). Basically, you start with an expression that consists of the sum operator itself and you expand it with the following three steps:

Check if the current value of the index i is less than or equal to the upper bound. If so, move to Step 2. Otherwise, terminate the whole process and replace the sum operator with the number 0.
Add the sum term with the current value of the index i to the expression and move to Step 3.
Increment the value of the index i by 1 and return to Step 1.

This might initially sound much more complicated than it actually is, so let’s look at a concrete example.

Expanding the sum (example)

Let’s take the expression from the image above and choose 0 as the lower bound and 2 as the upper bound. To start, we can simply set the expression equal to itself:

$\sum_{i=0}^{2} x_i = \sum_{i=0}^{2} x_i$

Now we can begin expanding the right-hand side. The initial value of i is 0 and Step 1 asks you to check if $0 \leq 2$

, which it is, so we move to Step 2. This step asks you to add $x_0$

to the expression and move to Step 3, which asks you to increment i by 1. The effect of these two steps is:

$\sum_{i=0}^{2} x_i = \left(\sum_{i=1}^{2} x_i\right) + x_0$

Then you’re told to go back to step 1 and go through the same process. Well, the current value of i (1) is still less than or equal to 2, so after going through steps 2 and 3 one more time, the expression becomes:

$\sum_{i=0}^{2} x_i = \left(\sum_{i=2}^{2} x_i\right) + x_0 + x_1$

Now we return to Step 1 and again pass through it because 2 is equal to the upper bound (which still satisfies the $\leq$

requirement). After going through steps 2 and 3 one more time, the expression becomes:

$\sum_{i=0}^{2} x_i = \left(\sum_{i=3}^{2} x_i\right) + x_0 + x_1 + x_2$

Now we go back to Step 1 but this time something’s different. The current value of the index (3) is greater than the upper bound 2, so instead of moving to Step 2, the instructions tell you to simply replace the sum operator part with 0 and stop the process. Therefore, the final expression becomes:

$\sum_{i=0}^{2} x_i = 0 + x_0 + x_1 + x_2$

But, as you know, 0 is the identity element of addition, so we can simply omit it from the expression. We’ve successfully completed the instructions and now we know that the expanded form of the sum is:

$\sum_{i=0}^{2} x_i = x_0 + x_1 + x_2$

The sum term

Now I want to focus my attention on the expression inside the sum operator. In the general formula and in the example above, the sum term was $x_i$ and you can think of the i subscript as an index. More specifically, it’s an index of a variable X representing a sequence of terms (more about sequences in the next section).

In principle, the sum term can be any expression you want. For example, if the sum term is $x_i = i$ , you get things like:

$\sum_{i=0}^{2} i = 0 + 1 + 2 = 3$

Or you can have fancier expressions like:

$\sum_{i=0}^{2} (i^2 + i^3) = (0^2 + 0^3) + (1^2 + 1^3) + (2^2 + 2^3) = 14$

In fact, the index i doesn’t even have to appear in the sum term! For example:

$\sum_{i=0}^{2} 4 = 4 + 4 + 4 = 3 \cdot 4$

If the sum term doesn’t depend on i, we will simply be adding the same number as we iterate over the values of i. Which reduces the sum operator to a fancy way of expressing multiplication by natural numbers. How many times we’re going to add it to itself will depend on the number of terms, which brings me to the next topic of this section.

How many terms are there?

First, let’s cover the degenerate case of expressions with no terms. When will this happen? Well, if the lower bound is a larger number than the upper bound, at the very first iteration you won’t be able to reach Step 2 of the instructions, since Step 1 will already ask you to replace the whole expression with a zero and stop. Which means that for all L > U:

$\sum_{i=L}^{U} x_i = 0$

This is usually called the empty sum and represents a sum with no terms.

But when $L \leq U$ , the sum will have at least one term. The exact number of terms is:

$\textrm{\# of terms} = (U - L) + 1$

Which means that $\sum_{i=1}^{1} x_i$

will have 1 term, $\sum_{i=3}^{7} x_i$

will have 5 terms, $\sum_{i=-1}^{2} x_i$

will have 4 terms, and so on.

This should make intuitive sense.

A note on infinite lower/upper bounds

Infinity symbol from lines and triangles, point connecting network on blue background

So far I’ve assumed that L and U are finite numbers. But often you might come across expressions like:

$\sum_{i=0}^{\infty} x_i$

Or even (less frequently) expressions like:

$\sum_{i=-\infty}^{5} x_i$

Or maybe even:

$\sum_{i=-\infty}^{\infty} x_i$

If the lower bound is negative infinity or the upper bound is positive infinity (or both), the sum will have an infinite number of terms. Now, I’m only mentioning this here so you know that such expressions exist and make sense. The name of a sum with infinite terms is a series, which is an extremely important concept in most of mathematics (including probability theory). I’m going to dedicate a special post to it soon.

For now, let’s ignore series and only focus on sums with a finite number of terms.

Shifting the index

I want to demonstrate the full flexibility of this notation to you. The general form of a sum operator expression I showed you was:

$\sum_{i=L}^{U} x_i$

But you might also come across expressions like:

$\sum_{i=L}^{U} x_{i+1}$

By adding 1 to each i inside the sum term, we’re essentially skipping ahead to the next item in the sequence at each iteration. For example, if we pick L=2 and U=4, the difference in how the two sums above expand is:

$\sum_{i=2}^{4} x_i = x_2 + x_3 + x_4$

$\sum_{i=2}^{4} x_{i+1} = x_3 + x_4 + x_5$

The effect is simply to shift the index by 1 to the right.

But you can do all sorts of manipulations to the index inside the sum term. Here’s a couple of more examples:

$\sum_{i=2}^{4} x_{i-2} = x_0 + x_1 + x_2$

$\sum_{i=2}^{4} x_{3i} = x_6 + x_9 + x_{12}$

In the first one, we’re shifting the index to the left by 2 and in the second one we’re adding every third element.

Implicit lower/upper bounds

Before moving to the next section, I want to show you a few examples of expressions with implicit notation. You will come across such expressions quite often and you should be familiar with what authors mean by them.

The general notation for a sum is:

$\sum_{i=L}^{U} x_i$

But sometimes you’ll see expressions where the lower bound or the upper bound are omitted:

$\sum_{i}^{U} x_i$

$\sum_{i=L} x_i$

Or sometimes even both could be omitted:

$\sum_{i} x_i$

As you know, mathematics doesn’t like ambiguity, so the only reason something would be omitted is if it was implied by the context or because a general statement is being made for arbitrary upper/lower bounds.

For example, the expression for expected value is typically written as:

$\sum_{i} x_i \cdot P(x_i)$

It’s implicit that you’re iterating over all elements of the sample space and usually there’s no need for the more explicit notation:

$\sum_{i=1}^N x_i \cdot P(x_i)$

Where N is the number of elements in the sample space.

The sum operator and sequences

I’ve described what the sum operator does mechanically, but what’s the point of having this notation in first place? Well, I already gave you the answer in the previous section, but let me elaborate here.

Ultimately, the sum operator is nothing but a compact way of expressing the sum of a sequence of numbers. If you think about it, the instructions are essentially telling you to iterate over the elements of a sequence and add them one by one. We achieve this by simply incrementing the current value of the index by 1 and plugging it into the sum term at each iteration. The index starts at the lower bound and stops at the upper bound:

$\sum_{i=L}^{U} x_i = x_L + x_{L + 1} + x_{L + 2} + ... + x_U$

If you’re familiar with programming languages (or if you read any Python simulation posts from my probability questions series), you probably find this conceptually similar to a for loop. And it is! In a way, the sum operator is a special case of a for loop where you’re adding the terms you’re iterating over. I say it’s a special case because you can do pretty much anything you want within a for loop, not just addition.

You can think of the sum operator as a generalization of repeated addition (or multiplication by a natural number). I demonstrated this to you with the example of a constant sum term. In the general case, for any constant c:

$\sum_{i=L}^{U} c = (U - L + 1) \cdot c$

The sum operator is a generalization of repeated addition because it allows you to represent repeated addition of changing terms. Or, like I said earlier, it allows you to add consecutive elements of a sequence. But what is a sequence anyway?

What is a sequence?

In mathematics, the term sequence generally refers to an ordered collection of items. For example, you can view a group of people waiting in line for something as a sequence. The person who’s first in line would be the first element (item) of the sequence, second in line would be the second element, and so on.

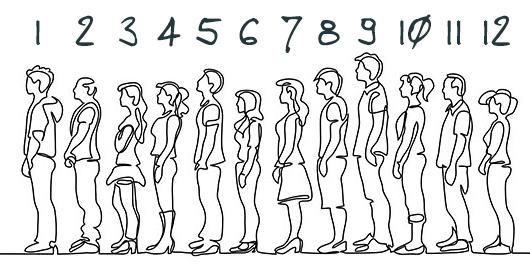
A mathematical sequence represented as 12 people waiting in line

When it comes to the sum operator, the sequences we’re interested in are numerical ones. That is, sequences whose elements are numbers. For example, here’s a sequence of the first 5 natural numbers:

0, 1, 2, 3, 4

And here’s a sequence with the first 6 odd natural numbers:

1, 3, 5, 7, 9, 11

Since the elements of sequences have a strict order and a particular count, the convention is to refer to an element by indexing with the natural numbers. From my post on natural numbers, you’ll remember that they start from 0, so it’s a common convention to start the index from 0 as well. And we write this index as a subscript of the variable representing an element of the sequence.

For example, let’s call the second sequence above X. Then, the 0th element of the sequence is actually the first item in the list, the 1st element is the second, and so on:

$x_0 = 1, x_1 = 3, x_2 = 5, x_3 = 7, x_4 = 9, x_5 = 11$

Starting the index from 0 (instead of 1) is a pretty common convention both in mathematics and computer science, so it’s definitely worth getting used to it.

Anyway, I think now you appreciate the point of sum operators. Using the index, we can express the sum of any subset of any sequence. For example, if we wanted to add the first 4 elements in the X sequence above, we would express it as:

$\sum_{i=0}^{3} x_i = x_0 + x_1 + x_2 + x_3 = 1 + 3 + 5 + 7$

Or if we want to sum the elements with index between 3 and 5 (last 3 elements), we would do:

$\sum_{i=3}^{5} x_i = x_3 + x_4 + x_5 = 7 + 9 + 11$

In general, you can express a sum of a sequence of any length using this compact notation.

Sequences as functions

In my introductory post to mathematical functions I told you that these are mathematical objects that relate two sets called the domain and the codomain. The elements of the domain are the inputs of the function and the elements of its codomain are called its outputs. If you haven’t already (and if you’re not familiar with functions), I encourage you to take a look at this post. Although, even without that you’ll be able to follow what I’m about to say.

You can think of sequences as functions whose domain is the set of natural numbers or any of its subsets. The regular convention for expressing functions is as f(x), where f is the function and x is a variable representing its input. But with sequences, a more common convention is to write the input as an index of a variable representing the codomain. If the variable is X and the index is i, you represent an element of the codomain of the sequence as $x_i$ .

Within this framework, you can define all sorts of sequences using a rule or a formula involving i. For example, you can define the i’th term of a sequence to be:

$x_i = i^2$

And, for example, the 3rd element of this sequence is:

$x_3 = 3^2 = 9$

The first 5 elements of this sequence are 0, 1, 4, 9, and 16.

By default, a sequence is defined for all natural numbers, which means it has infinitely many elements. But you can always create a finite sequence by choosing a lower and an upper bound for the index, just like we do with the sum operator.

Anyway, I’m going to talk more about sequences in my upcoming post on common mathematical functions. For now, let’s just look at a few more examples to get a better intuition.

Example sequences and their sums

In the previous sections, I showed you the definition of three example sequences:

$x_i = i$ , whose terms are 0, 1, 2, 3…
$y_i = i^2$ , whose terms are 0, 1, 4, 9…
$z_i = i^2 + i^3$ , whose terms are 0, 2, 12, 36…

There’s nothing stopping you from coming up with any rule defining any sequence. Anything goes, as long as you can express it mathematically. Let’s look at a few more examples, with the first 4 terms of each:

$a_i = 7$ , first terms: 7, 7, 7, 7 (constant term)
$b_i = i^2 + 3$ , first terms: 3, 4, 7, 12
$c_i = \frac{1}{i+1}$ , first terms: $1, \frac{1}{2}, \frac{1}{3}, \frac{1}{4}$
$d_i = 2^i$ , first terms: 1, 2, 4, 8

Now just for fun, let’s calculate the sum of the first 3 items of, say, the B sequence:

$\sum_{i=0}^{2} b_i = \sum_{i=0}^{2} (i^2 + 3) = 3 + 4 + 7 = 14$

If you like, calculate the sum of the first 10 terms of the A, C, and D sequences as an exercise. And, as another exercise, can you guess which sequences the following two formulas represent? Let’s call them the E sequence and the O sequence, respectively:

$e_i = 2i$

$o_i = 2i + 1$

What is the sum of the first 10 terms of each of them?

Sums with closed-form solutions

In the general case, to calculate the value of an expression with a sum operator you need to manually add all terms in the sequence over which you’re iterating. However, you can derive formulas for directly calculating the sums of some special sequences.

Here I want to give you (without proof) a few of the most common examples of such closed-form solutions you’ll come across. I’m going to prove some of these in my post on series but for now just know that the following formulas exist. For all of them we’re going to assume the index starts from 0 but later I’m going to show you how to easily derive the formulas for any lower bound.

First, here’s a formula for the sum of the first n+1 natural numbers:

$\sum_{i=0}^{n} i = \frac{n(n+1)}{2}$

For example:

$\sum_{i=0}^{3} i = \frac{3 \cdot (3+1)}{2} = 6$

Which is exactly what you’d get if you did the sum manually:

$\sum_{i=0}^{3} i = 0 + 1 + 2 + 3 = 6$

Try it out with some other values of n to see that it works!

Now, remember the E and O sequences I left you as an exercise? In case you haven’t figured it out, those are the sequences of even and odd natural numbers. The formulas for their sums are:

$\sum_{i=0}^{n} 2i = n(n+1)$

$\sum_{i=0}^{n} (2i + 1) = (n+1)^2$

Closed-form solutions also exist for the sequences defined by $x_i = i^2$

and $x_i = i^3$

$\sum_{i=0}^{n} i^2 = \frac{n(n+1)(2n+1)}{6}$

$\sum_{i=0}^{n} i^3 = \frac{n^2(n+1)^2}{4}$

Generally, you can derive a closed-form solution for all sequences defined by raising the index to the power of a positive integer, but I won’t go into this here, since it requires some more advanced math tools to express. But for those of you who are curious, check out the Wikipedia article on Faulhaber’s formula.

There’s also a closed-form solution to sequences in the form $x_i = c^i$ , where c can be any constant:

$\sum_{i=0}^{n} c^i = \frac{c^{n+1} - 1}{c-1}$

For example:

$\sum_{i=0}^{10} 3^i = \frac{3^{11} - 1}{3 - 1} = 88573$

Finally, here’s a formula for the binomial theorem which I introduced in my post about the binomial distribution:

$\sum_{i=0}^{n} x^{n-i}y^i = (x + y)^n$

Double sums

By now you must have a good enough understanding and feel for the sum operator and the flexibility around the sum term. You can pretty much have any expression inside, which may or may not refer to the index. Now let’s stretch our understanding of “pretty much any expression” even more.

What if the sum term itself was another sum, having its own index and lower/upper bounds? Can we do that?

Sure we can, why not? Take a look at this expression:

$\sum_{i=L_1}^{U_1} \left(\sum_{j=L_2}^{U_2} x_j\right)$

The sum term of the outer sum is another sum which has a different letter for its index (j, instead of i). Also, notice that instead of L and U, now we have L₁/U₁ and L₂/U₂, since the lower/upper bounds of the two sums don’t have to be the same.

I included the parentheses to make the expression more readable, but the common convention is to express double sums without them:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_j$

Anyway, how do we expand an expression like that? Well, it’s the same idea as with any other sum term. Only, for each iteration of the outer sum, we are going to have a sum, instead of a single number. Let’s plug in some actual values for L₁/U₁ and L₂/U₂ to see what I’m talking about:

$\sum_{i=0}^{1} \sum_{j=0}^{2} x_j = (x_0 + x_1 + x_2) + (x_0 + x_1 + x_2)$

The index i of the outer sum will take the values of 0 and 1, so it will have two terms. On the other hand, each of the terms will be the inner sum, which itself consists of 3 terms (where j takes the values 0, 1, and 2). But since we’re adding the same sum twice, the expanded form can also be written as:

$\sum_{i=0}^{1} \sum_{j=0}^{2} x_j = 2 \cdot (x_0 + x_1 + x_2)$

Because the inner sum is a constant with respect to the outer sum, any such expression reduces to:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_j = (U_1 - L_1 + 1) \cdot \sum_{j=L_2}^{U_2} x_j$

When the sum term depends on both indices

If all that double sums could do was represent a sum multiplied by a constant, that would be kind of an overkill, wouldn’t it? Well, the full power of double sums becomes apparent when the sum term is dependent on the indices of both sums. Let’s see how.

In my introductory post to functions the focus was on functions that take a single input value. However, in the general case, a function can take an arbitrary number of inputs. While the topic of multivariable functions is extremely important by itself, I won’t go into too much detail here. I’m just going to show you a few examples in the context of sequences.

Take a look at this definition:

$x_{i, j} = 2i + 3j$

Here’s a couple of examples for evaluating this function with concrete numbers:

$x_{1, 3} = 2 \cdot 1 + 3 \cdot 3 = 11$

$x_{7, 4} = 2 \cdot 7 + 3 \cdot 4 = 26$

You can think of such functions as two-dimensional sequences that look like tables. The rows of the table are indexed by the first variable (i) and the columns are indexed by the second variable (j):

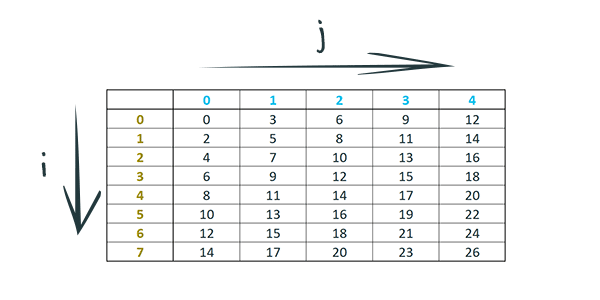
A two dimensional sequence in the form of a 8 by 5 table with numeric values

Then, the $x_{i, j}$ element of this sequence is the cell corresponding to row i and column j.

If we now want to express the sum of a particular subset of this table, we could do things like:

$\sum_{i=0}^{1} \sum_{j=0}^{2} x_{i, j} = \sum_{i=0}^{1} \sum_{j=0}^{2} (2i + 3j) =$

$(2 \cdot 0 + 3 \cdot 0) + (2 \cdot 0 + 3 \cdot 1) + (2 \cdot 0 + 3 \cdot 2)$

$+ (2 \cdot 1 + 3 \cdot 0) + (2 \cdot 1 + 3 \cdot 1) + (2 \cdot 1 + 3 \cdot 2)$

Notice how for each value of i we iterate over every value of j. In the above example i ranges from 0 to 1 and j ranges from 0 to 2, which essentially corresponds to the following cells in the table:

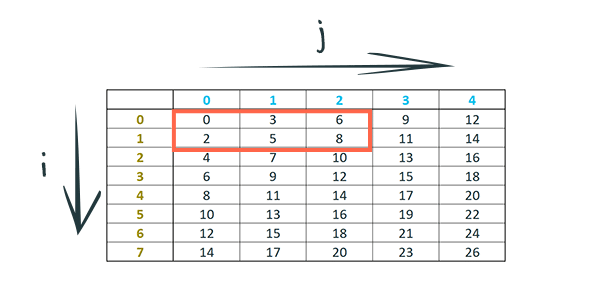
A two dimensional sequence in the form of a 8 by 5 table with numeric values. A subset of the cells are highlighted to indicate they are added together

Here’s another sum of the same sequence but with different boundaries:

$\sum_{i=2}^{6} \sum_{j=1}^{2} (2i + 3j)$

Which instructs us to add the following cells:

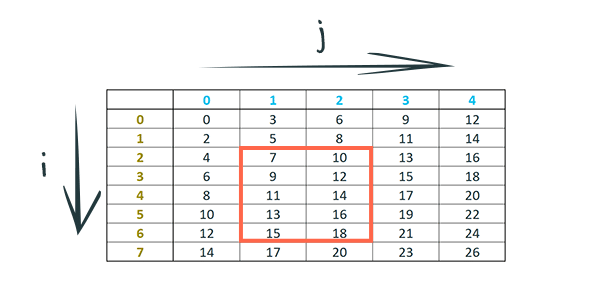
When the inner sum bounds depend on the outer sum’s index

To show you the full flexibility of this notation, I want to give a few examples of more interesting expressions. Take a look at this double sum:

$\sum_{i=0}^{2} \sum_{j=0}^{i} x_{i,j}$

What’s interesting about it? Well, the upper bound of the inner sum is not a constant but is set equal to the value of the outer sum’s index! Which means that the inner sum will have a different upper bound for each iteration of the outer sum. Let’s expand the above sum to see how it works:

$\sum_{i=0}^{2} \sum_{j=0}^{i} x_{i,j} = x_{0,0}$

$+ x_{1,0} + x_{1,1}$

$+ x_{2,0} + x_{2,1} + x_{2,2}$

You can also have the case where the lower bound depends on the outer sum’s index:

$\sum_{i=0}^{2} \sum_{j=i}^{3} x_{i,j}$

Which would expand like:

$\sum_{i=0}^{2} \sum_{j=i}^{3} x_{i,j} = x_{0,0} + x_{0,1} + x_{0,2} + x_{0,3}$

$+ x_{1,1} + x_{1,2} + x_{1,3}$

$+ x_{2,2} + x_{2,3}$

You can even have expressions as fancy as:

$\sum_{i=0}^{2} \sum_{j=i+1}^{i^2} x_{i,j}$

Here both the lower and upper bounds depend on the outer sum’s index. As you can see, the bounds can be arbitrary functions of the index as well. As an exercise, try to expand this expression yourself.

You’ll sometimes come across the term nested sums to describe expressions like the ones above.

Generalizing to multiple sums

To conclude this section, let me tell you about something many of you have already thought about. If the sum term of an expression can itself be a sum, can it also be a double sum? The answer is a resounding “yes”. And, like the case for double sums, the interesting cases here are when the inner expression depends on all indices.

For example, here’s what a triple sum generally looks like:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} \sum_{k=L_3}^{U_3} x_{i,j,k}$

And here’s what a quadruple sum looks like:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} \sum_{k=L_3}^{U_3} \sum_{l=L_4}^{U_4} x_{i,j,k, l}$

Of course, you can have expressions with as many sums as you like. By analogy to double sums representing sums of elements of two-dimensional sequences, you can think of triple sums as representing sums of three-dimensional sequences, quadruple sums of four-dimensional sequences, and so on.

The general principle for expanding such expressions is the same as with double sums. You increment the index of the innermost sum the fastest and that of the outermost sum the slowest. For example, in triple sums, for every value of the outermost sum’s index you will iterate over every value of the middle sum’s index. And for every value of the middle sum’s index you will iterate over every value of the innermost sum’s index:

$\sum_{i=0}^{1} \sum_{j=0}^{1} \sum_{k=0}^{1} x_{i,j,k} =$

$x_{0,0,0} + x_{0,0,1} + x_{0,1,0} + x_{0,1,1}$

$+ x_{1,0,0} + x_{1,0,1} + x_{1,1,0} + x_{1,1,1}$

Also, just like with double sums, you can have expressions where the lower/upper bounds of the inner sums depend on one or more of the indices of the outer sums (nested sums). For example:

$\sum_{i=0}^{5} \sum_{j=0}^{i} \sum_{k=0}^{j} x_{i,j,k}$

Properties of the sum operator

In the final section of today’s post, I want to show you five properties of the sum operator. These properties allow you to manipulate expressions involving sums, which is often useful for things like simplifying expressions and proving formulas.

All of these properties ultimately derive from the properties of basic arithmetic operations (which I covered extensively in my post on the topic). In particular, all of the properties that I’m about to show you are derived from the commutative and associative properties of addition and multiplication, as well as the distributive property of multiplication over addition.

The commutative property allows you to switch the order of the terms in addition and multiplication and states that, for any two numbers a and b:

$a + b = b +a$

$a \cdot b = b \cdot a$

The associative property tells you that the order in which you apply the same operations on 3 (or more) numbers doesn’t matter. It essentially allows you to drop parentheses from expressions involving more than 2 numbers. The property states that, for any three numbers a, b, and c:

$(a + b) + c = a + (b + c) = a + b + c$

$(a \cdot b) \cdot c = a \cdot (b \cdot c) = a \cdot b \cdot c$

Finally, the distributive property of multiplication over addition states that, for any three numbers a, b, and c:

$a \cdot (b + c) = a \cdot b + a \cdot c$

$(b + c) \cdot a = b \cdot a + c \cdot a$

Take a look at the post I linked above for more intuition on these properties. Now let’s use them to derive the five properties of the sum operator.

Splitting sums

Sometimes you may want to split a single sum into two separate sums using an intermediate bound. For example, take the following sum:

$\sum_{i=5}^{10} x_i = x_5 + x_6 + x_7 + x_8 + x_9 + x_{10}$

The associative property of addition allows you to split the right-hand side in two parts and represent each as a separate sum:

$x_5 + x_6 + x_7 + x_8 + x_9 + x_{10} = (x_5 + x_6 + x_7 + x_8) + (x_9 + x_{10})$

$= \sum_{i=5}^{8} x_i + \sum_{i=9}^{10} x_i$

Generally, for any lower and upper bounds L and U, you can pick any intermediate number I, where $L < I < U$

, and split a sum in two parts:

$\sum_{i=L}^{U} x_i = \sum_{i=L}^{I-1} x_i + \sum_{i=I}^{U} x_i$

Of course, there’s nothing stopping you from splitting it into more parts. For example, if you want to split a sum in three parts, you can pick two intermediate values $I_1$

and $I_2$

, such that $L < I_1 < I_2 < U$

. Then you can split the sum like so:

$\sum_{i=L}^{U} x_i = \sum_{i=L}^{I_1-1} x_i + \sum_{i=I_1}^{I_2-1} x_i + \sum_{i=I_2}^{U} x_i$

Example application of splitting a sum

Now I want to show you an extremely useful application of this property. Remember earlier I listed a few closed-form solutions for sums of certain sequences? For example:

$\sum_{i=0}^{n} 2i = n(n+1)$

You’ll notice that all formulas in that section have the starting value of the index (the lower bound) at 0. But what if someone gave you an expression like:

$\sum_{i=5}^{n} 2i$

Even though you can’t directly apply the above formula, there’s a really neat trick for obtaining a formula for any lower bound L, if you already have a formula for L=0.
First, let’s write the general equation for splitting a sum for the case L=0:

$\sum_{i=0}^{U} x_i = \sum_{i=0}^{I-1} x_i + \sum_{k=I}^{U} x_i$

If we subtract $\sum_{i=0}^{I-1} x_i$

from both sides of this equation, we get the equation:

$\sum_{k=I}^{U} x_i = \sum_{i=0}^{U} x_i - \sum_{i=0}^{I-1} x_i$

Do you see what happened? This manipulation allows you to express a sum with any lower bound in terms of a difference of sums whose lower bound is 0. Which, in turn, allows you to obtain a closed-form solution for any sum, regardless of its lower bound (as long as the closed-form solution exists for L=0).

Coming back to the example above, now we can derive a general formula for any lower bound:

$\sum_{i=L}^{n} 2i =\sum_{i=0}^{n} 2i - \sum_{i=0}^{L-1} 2i$

$\sum_{i=L}^{n} 2i =n(n+1) - L(L-1)$

Plugging L=5:

$\sum_{i=5}^{n} 2i =n(n+1) - 20$

In the general case, if the closed-form solution for L=0 is a function f of the upper bound U, the closed form solution for an arbitrary L is:

$\sum_{k=L}^{U} x_i = f(U) - f(L-1)$

Constant terms

The next property I want to show you comes directly from the distributive property of multiplication over addition. Multiplying a polynomial of any number of terms by a constant c gives the following identity:

$c(x_0 + x_1 + ... + x_U) = cx_0 + cx_1 + ... + cx_U$

For example, with only three terms:

$c(x_0 + x_1 + x_2) = cx_0 + cx_1 + cx_2$

Notice that we can express the left-hand side as:

$c(x_0 + x_1 + ... + x_U) = c \sum_{i=0}^{U} x_i$

And the right-hand side as:

$cx_0 + cx_1 + ... + cx_U = \sum_{i=0}^{U} c x_i$

From which we derive:

$\sum_{i=0}^{U} c x_i = c \sum_{i=0}^{U} x_i$

Or, more generally for any lower bound L:

$\sum_{i=L}^{U} c x_i = c \sum_{i=L}^{U} x_i$

Basically, anything inside the sum operator that doesn’t depend on the index i is a constant in the context of that sum. So, this property simply states that such constant multipliers can be taken out of the sum without changing the final value.

Adding and subtracting sums

Another useful property of the sum operator is related to the commutative and associative properties of addition.

Say we have the sum:

$\sum_{i=0}^{2} (x_i + y_i) = (x_0 + y_0) + (x_1 + y_1) + (x_2 + y_2)$

The commutative property allows us to rearrange the terms and get:

$(x_0 + y_0) + (x_1 + y_1) + (x_2 + y_2) = (x_0 + x_1 + x_2) + (y_0 + y_1 + y_2)$

$= \sum_{i=0}^{2} x_i + \sum_{i=0}^{2} y_i$

On the left-hand side, the terms are grouped by their index (all 0s + all 1s + all 2s), whereas on the right-hand side they’re grouped by variables (all x’s + all y’s). In this case, the L and U parameters are 0 and 2 but you see that we can easily generalize to any values:

$\sum_{i=L}^{U} (x_i + y_i) = \sum_{i=L}^{U} x_i + \sum_{i=L}^{U} y_i$

Furthermore, if we represent subtraction as addition with negative numbers, we can generalize the rule to subtracting sums as well:

$\sum_{i=L}^{U} (x_i - y_i) = \sum_{i=L}^{U} x_i - \sum_{i=L}^{U} y_i$

Or, more generally:

$\sum_{i=L}^{U} (x_i \pm y_i) = \sum_{i=L}^{U} x_i \pm \sum_{i=L}^{U} y_i$

You can use this property to represent sums with complex expressions as addition of simpler sums, which is often useful in proving formulas. Of course, sometimes you might use it in the other direction to merge two sums of two independent sequences X and Y:

$\sum_{i=L}^{U} x_i \pm \sum_{i=L}^{U} y_i = \sum_{i=L}^{U} (x_i \pm y_i)$

It’s important to note that this property only works if the X and Y sequences are of equal length. That is, if the two sums on the left have the same number of terms.

Multiplying sums

The next property I want to show you also comes from the distributive property of multiplication over addition. Say you have two independent sequences X and Y which may or may not be of equal length. Their respective sums are:

$\sum_{i=L_1}^{U_1} x_i = x_{L_1} + x_{L_1+1} + ... + x_{U_1}$

$\sum_{j=L_2}^{U_2} y_j = y_{L_2} + y_{L_2+1} + ... + y_{U_2}$

What happens if we multiply these two sums?

$\sum_{i=L_1}^{U_1} x_i \cdot \sum_{j=L_2}^{U_2} y_j = ?$

In general, when you’re multiplying two polynomials, the expanded form is achieved by multiplying each term of the first polynomial by each term of the second. This is a direct consequence of the distributive property of multiplication:

The formula of the distributive property of multiplication

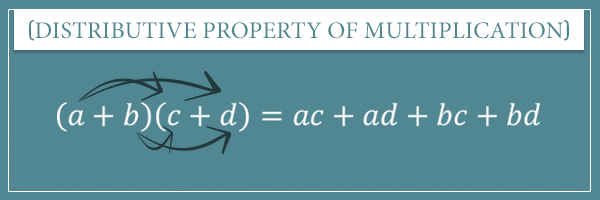
For example:

$\sum_{i=0}^{2} x_i \cdot \sum_{j=0}^{1} y_j = (x_0 + x_1 +x_2) \cdot (y_0 + y_1)$

$= x_0 \cdot y_0 + x_0 \cdot y_1+ x_1 \cdot y_0 + x_1 \cdot y_1 + x_2 \cdot y_0 + x_2 \cdot y_1$

In the general case, for any L and U:

$\sum_{i=L_1}^{U_1} x_i \cdot \sum_{j=L_2}^{U_2} y_j = (x_{L_1} + x_{L_1+1} + ... + x_{U_1}) \cdot (y_{L_2} + y_{L_2+1} + ... + y_{U_2})$

$= x_{L_1} \cdot y_{L_2} + x_{L_1} \cdot y_{L_2+1} + ... + x_{L_1} \cdot y_{U_2} + ... + x_{U_1} \cdot y_{U_2}$

In words, the expanded form of the product of the two sums consists of terms in the form of $x_i \cdot y_j$

where i ranges from L₁ to U₁ and j ranges from L₂ to U₂. But isn’t there another way to express the right-hand side with our compact notation?

Well, let’s define a new sequence W which is the product of the two sequences:

$w_{i, j} = x_i \cdot y_j$

If we sum all elements of the two-dimensional sequence W, we get the double sum expression:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} w_{i, j} = \sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_i \cdot y_j$

$= x_{L_1} \cdot y_{L_2} + x_{L_1} \cdot y_{L_2+1} + ... + x_{L_1} \cdot y_{U_2} + ... + x_{U_1} \cdot y_{U_2}$

Which expands exactly like the product of the individual sums!

The intuition here is that we’re combining each value of i with every value of j just like we’re multiplying each term from the first polynomial with every term of the second. This leads to the general property:

$\sum_{i=L_1}^{U_1} x_i \cdot \sum_{j=L_2}^{U_2} y_j = \sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_i \cdot y_j$

Remember that the property related to adding/subtracting sums only works if the two sums are of equal length. By contrast, as I just demonstrated, the property for multiplying sums works even if they don’t have the same length.

Lastly, this property naturally generalizes to the product of an arbitrary number of sums. For example, with three sums:

$\sum_{i=L_1}^{U_1} x_i \cdot \sum_{j=L_2}^{U_2} y_j \cdot \sum_{k=L_3}^{U_3} z_k = \sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} \sum_{k=L_3}^{U_3} x_i \cdot y_j \cdot z_k$

And more generally, for an arbitrary number of sums (N):

$\sum_{i_1=L_1}^{U_1} x_{i_1} \cdot ... \cdot \sum_{i_N=L_N}^{U_N} x_{i_N} = \sum_{i_1=L_1}^{U_1} ... \sum_{i_N=L_N}^{U_N} x_{i_1} \cdot ... \cdot x_{i_N}$

By the way, if you find these general expressions hard to read, don’t worry about it. It takes a little practice but with time you’ll learn to read them much more easily.

Shuffling multiple sums

The last property I want to show you is also related to multiple sums. Not just the ones representing products of individual sums, but any kind. It follows directly from the commutative and associative properties of addition.

The property says that when you have multiple sums whose bounds are independent of each other’s indices, you can switch their order however you like. For example, with double sums you have the following identity:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_{i, j} = \sum_{j=L_2}^{U_2} \sum_{i=L_1}^{U_1} x_{i, j}$

In words, you can iterate over every every value of j for every value of i, or you can iterate over every value of i for every value of j — the result will be the same. Why does it work?

Let’s pick concrete numbers for the bounds and expand the double sum to gain some intuition:

$\sum_{i=0}^{1} \sum_{j=2}^{4} x_{i, j} = (x_{0,2} + x_{0,3} + x_{0,4}) + (x_{1,2} + x_{1,3} + x_{1,4})$

Now let’s change the order of the sum operators on the right-hand side and expand again:

$\sum_{j=2}^{4} \sum_{i=0}^{1} x_{i, j} = (x_{0,2} + x_{1,2}) + (x_{0,3} + x_{1,3}) + (x_{0,4} + x_{1,4})$

Notice that in both cases the same terms appear on the right-hand sides, but in different order. Well, from the associative and commutative properties of addition we know that this doesn’t change the final value and they’re equal to each other. And it should be intuitive that the same thing holds for any choice for the lower and upper bounds of the two sums.

This property also naturally generalizes to more than two sums. For example, with three sums:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} \sum_{k=L_3}^{U_3} x_{i, j, k} = \sum_{i=L_1}^{U_1} \sum_{k=L_3}^{U_3} \sum_{j=L_2}^{U_2} x_{i, j, k} = \sum_{j=L_2}^{U_2} \sum_{i=L_1}^{U_1} \sum_{k=L_3}^{U_3} x_{i, j, k}$

$= \sum_{k=L_3}^{U_3} \sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_{i, j, k} = \sum_{j=L_2}^{U_2} \sum_{k=L_3}^{U_3} \sum_{i=L_1}^{U_1} x_{i, j, k} = \sum_{k=L_3}^{U_3} \sum_{j=L_2}^{U_2} \sum_{i=L_1}^{U_1} x_{i, j, k}$

However, I said it in the beginning and I’ll say it again. This property only works if the lower and upper bounds of each sum are independent of the indices of the other sums!

Summary

Phew, this was a long post, wasn’t it? I hope it wasn’t too exhausting to read and you found it easy to follow.

My goal here was to give you all the crucial information about the sum operator you’re going to need. Not that I can ever fit literally everything about a topic in a single post, but the things you learned today should get you through most of your encounters with this notation. And, if you need to, they will allow you to easily learn the more advanced stuff that I didn’t go into.

Notation

The sum operator is nothing but a compact notation for expressing repeated addition of consecutive elements of a sequence. The notation consists of a sum term, an index variable (which often appears in the sum term), as well as a lower and an upper bound for the index:

The way we expand a sum operator expression is by iterating over the values of the index and, for each, adding a new term with the current value of the index:

$\sum_{i=L}^{U} x_i = x_L + x_{L + 1} + x_{L + 2} + ... + x_U$

The expanded form of the sum will have a number of terms equal to one more than the difference between the upper bound and the lower bound:

$\textrm{\# of terms} = (U - L) + 1$

I also told you that sometimes the lower and upper bounds can be omitted from the expression if their values are implied from the context:

$\sum_{i} x_i$

Sequences

When it comes to the sum term itself, I told you that it represents the i’th term of a sequence. A sequence is a function whose domain is the set (or a subset) of natural numbers . For many sequences you’ll have the i’th term defined by a formula, like $x_i = i^2$ , or more generally:

$x_i = f(i)$

Where f can be any function of i.

I also showed you a few closed-form solutions to the sums of certain sequences, such as:

$\sum_{i=0}^{n} i = \frac{n(n+1)}{2}$

More generally, the sums of some sequences have closed-form solutions that can be expressed as a function of their lower and/or upper bounds:

$\sum_{i=L}^{U} x_i = g(L, U)$

I also showed you double sum expressions which expand by iterating over every value of the inner sum’s index for every value of the outer sum’s index:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_{i, j} = x_{L_1, L_2} + x_{L_1, L_2 + 1} + ... + x_{L_1, U_2} + ... + x_{U_1, U_2}$

You can think of the sum term as an element of a two-dimensional sequence. And you can similarly have triple, quadruple, or generally any multiple sum expression which represent summing elements of higher dimensional sequences.

I also showed you examples of double (or multiple) sum expressions where the inner sums’ bounds can be some functions of (dependent on) the outer sums’ indices:

$\sum_{i=L}^{U} \sum_{j=f(i)}^{g(i)} x_{i, j}$

The properties

Finally, I showed you five useful properties that allow you to simplify or otherwise manipulate sum operator expressions.

Splitting a sum into 2 sums:

$\sum_{i=L}^{U} x_i = \sum_{i=L}^{I-1} x_i + \sum_{i=I}^{U} x_i$

Multiplying a sum by a constant:

$c \sum_{i=L}^{U} x_i = \sum_{i=L}^{U} c x_i$

Adding or subtracting sums:

$\sum_{i=L}^{U} x_i \pm \sum_{i=L}^{U} y_i = \sum_{i=L}^{U} (x_i \pm y_i)$

Multiplying sums:

$\sum_{i_1=L_1}^{U_1} x_{i_1} \cdot ... \cdot \sum_{i_N=L_N}^{U_N} x_{i_N} = \sum_{i_1=L_1}^{U_1} ... \sum_{i_N=L_N}^{U_N} x_{i_1} \cdot ... \cdot x_{i_N}$

And changing the order of individual sums in multiple sum expressions:

$\sum_{i=L_1}^{U_1} \sum_{j=L_2}^{U_2} x_{i, j} = \sum_{j=L_2}^{U_2} \sum_{i=L_1}^{U_1} x_{i, j}$

As always, feel free to leave any questions or comments in the comment section below. Until next time!

Comments

James Kennedy says

February 9, 2024 at 7:00 pm

Thank you! You expressed the rules of order in both concise and thorough ways. Easy on the sanity! You extended the rules to multiple sums (3 and more sums) concisely and thoroughly, …and that was most unique and helpful compared to all the other online sources I reviewed over the last 6 hours!
Again, Thank you for preserving my sanity regarding multiple sums (Sigma) operations! Your presentation is concise and thorough.

The anatomy of the sum operator

Expanding the sum (example)

The sum term

How many terms are there?

A note on infinite lower/upper bounds

Shifting the index

Implicit lower/upper bounds

The sum operator and sequences

What is a sequence?

Sequences as functions

Example sequences and their sums

Sums with closed-form solutions

Double sums

When the sum term depends on both indices

When the inner sum bounds depend on the outer sum’s index

Generalizing to multiple sums

Properties of the sum operator

Splitting sums

Example application of splitting a sum

Constant terms

Adding and subtracting sums

Multiplying sums

Shuffling multiple sums

Summary

Notation

Sequences

The properties

Comments

Leave a Reply Cancel reply