Cryptography: Historical Introduction & Combinatoric Analysis (Series)

Hi everyone, and welcome to my series on cryptography!

Initially, I started writing this as a single post, but as I was planning what I wanted to include, and seeing how long it would become, I decided it’s best to split it into separate posts.

Cryptography is the study of techniques and procedures, such as using codes and ciphers, for secure (secret) communication between two or more agents. More specifically, it deals with finding sophisticated ways of hiding the true content of messages exchanged between communicators. People use cryptography in military and diplomatic communication, password protection, securing online transactions, as well as in any other context where some secret information needs to be protected from being accessed or understood.

As you’ll see in future posts, probability theory too can play an important role in cryptography.

Overview of the series

The post you’re currently reading is the introductory post (part 1) of the series. And here are the 6 posts that introduce different cryptographic codes and ciphers from different periods of human history:

• Ancient cryptography (part 2)
  • The column cipher
  • The Caesar cipher
• Polyalphabetic ciphers and cryptography before the 20th century (part 3)
  • Alberti’s cipher
  • Trithemius’ cipher
  • Bellaso’s cipher
  • The Vigenère cipher
  • The autokey cipher
  • The one-time pad
• The birth and evolution of cryptographic codes (part 4)
  • Alberti’s code
  • The nomenclator
  • Smith’s code
  • Slater’s code
  • The route cipher
  • Baravelli’s code
• Cryptography during World War I (part 5)
  • Playfair cipher
  • Interrupted columnar transposition cipher
  • Turning grilles cipher
  • ADFGX and ADFGVX ciphers
  • German diplomatic codes
• Cryptography with machines, before and during World War II (part 6)
  • Jefferson’s cipher
  • Wadsworth’s cipher
  • Vernam’s cipher (one-time pad implementation)
  • The Enigma machine
• Cryptography in the age of computers (part 7)
  • Symmetric-key cryptography
  • Public-key cryptography
  • Hashing functions

The 6 titles above are going to become active links one by one, as I publish the posts in the above order in the next few weeks. My plan for this series is to give an extensive overview of cryptography. And, to really get you in the mood, I’m going to give some decent historical context around the usage of the codes and ciphers I show you. I think you’ll find this very interesting!

I’m also going to use this series as a nice exercise in combinatorics. More specifically, I’m going to analyze each of the codes and ciphers in terms of their combinatoric complexity and security (ability to resist brute-force attacks).

So, after completing the series, not only will you become a junior cryptographer, but in the meantime you’ll also have a good opportunity to practice some fundamental concepts from combinatorics!

And you’ll hear interesting stories that will give you a good intuition about the historical importance of cryptography.

Combinatorics: a short recap

Before I begin with cryptography, let me first give you a brief recap of combinatorics. I introduced combinatorics and the basic concepts from the field in an early post.

So, what is it? Well, a short and informal definition of combinatorics is that it’s a field concerned with counting things. Things like the number of ways in which you can arrange a set of N items. Or the number of unique combinations of length K you can make from a set of N items.

I introduced the rule of product with which I derived a lot of formulas from combinatorics, such as:

• permutations
• partial permutations
• combinations
• the Binomial coefficient
• the cardinality (number of elements) of a set’s power set

Alright, so what is the rule of product?

Well, imagine you have a set of N objects and another set of M objects. And imagine you want to create pairs with elements from the two sets. That is, pairs in which one of the objects is from the first set and the other is from the second set.

The rule of product simply states that the number of (unique) such pairs you can create is equal to N times M. For example, if the first set is {A, B}, and the second set it {1, 2, 3}, then there are unique pairs you can form:

• (A, 1), (A, 2), (A, 3)
• (B, 1), (B, 2), (B, 3)

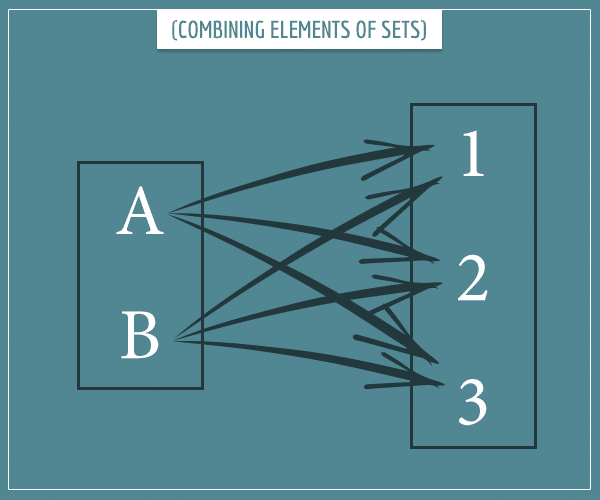
It’s really that simple (just count the arrows)! But as simple as it is, the rule of product underlies a big part of combinatorics.

Just like I used the rule of product to derive combinatorics formulas in my introductory post, in this series I’m going to use it to analyze the combinatoric complexity of codes and ciphers.

Combinatoric complexity of cryptographic codes and ciphers

More specifically, we’re going to look at how difficult it is to crack codes and ciphers using a brute-force attack. A brute-force attack on a cipher or a code essentially means trying to guess the right key or code-meaning association by individually checking all possibilities.

If you don’t know what I mean by a “key” or a “code-meaning association”, you’ll learn soon enough. For now, let me give you another example. If you try to crack someone’s password with a brute-force attack, that means you need to try all possible character combinations of every length (up to the maximum allowed).

In other words, a brute-force attack doesn’t require any sophisticated methods or algorithms. Hence, this is also the most basic test for any code or cipher. Because, if a code/cipher isn’t secure enough to endure a brute-force attack, it just isn’t secure enough for any serious usage.

In my analysis, I’m going to make the following assumption:

The enemy knows the system.

Claude Shannon

This quote is by the legendary US cryptographer Claude Shannon and it’s sometimes called Shannon’s maxim. Basically, it states that a cryptographic system should be secure enough even if its details were completely known (except for the variable key). The Kerckhoffs principle is a similar statement the Dutch cryptographer Auguste Kerckhoffs made a century before Shannon.

So, when doing combinatoric security evaluation of the codes and ciphers in this series, I’m going to assume we know how they work, and only assume lack of knowledge about their keys. And, after the evaluation, I’m going to give each of them a security score on a scale from 1 to 10.

If you don’t have previous knowledge about combinatorics, I recommend you go through my introductory post at some point.

Now let’s see what cryptography is all about.

Introduction to cryptography

Do you know anything about cryptography? No? Well, don’t worry. I’m not going to assume any prior knowledge and I’m going to introduce all relevant concepts you’ll need to follow this series.

In cryptographic literature, it’s common to use the names Alice and Bob for any two secretly communicating agents. This tradition started from a paper by the famous cryptographers Ron Rivest, Adi Shamir, and Leonard Adleman. If you’re curious, here’s a link.

Another convention is to use the fictional character Eve to represent an unwanted “eavesdropper” interested in learning the secret information Alice and Bob are exchanging.

So, to make this post fun, I’m going to stick to these conventions too.

Now let’s try to put ourselves in the shoes of people from a long time ago, before they knew anything about cryptography.

Setting up a cryptographic scenario

Here we have Alice and Bob trying to find a way to exchange messages between each other so that nobody else can read them. Let’s say Alice and Bob are two army generals from around 3000 BCE and they’re in a war against another army (around that time people hardly had any concept of cryptography).

So, they’re about to split and want to be able to communicate things like military strategy, tactics, and intelligence through exchanging letters carried by messengers. Therefore, they need to come up with a method of writing these messages in a secret way. Even if enemy forces capture a messenger and find the letter with the message, the enemy general Eve shouldn’t be able to understand its contents. Remember, Alice and Bob don’t know anything about cryptography yet!

If you like, before you continue reading, take a moment and try to come up with some methods yourself. Say you and your friend want to exchange letters with messages that only you two can understand. And anybody else reading those letters shouldn’t be able to make any sense of the contents. How would you do it?

Alright, assuming you’ve given it some thought, here’s my own reasoning.

Inventing cryptography from scratch

If I’m Alice or Bob, I might try coming up with a code system where specific words represent full sentences. For example, they can send each other letters with words for colors. Each color can have a specific meaning only Alice and Bob know. For example, “red” can mean “we are surrounded”, “green” can mean “attack at dawn”, and so on.

Would this method work? Well, although the number of messages they can send with it is quite small, at first glance it seems to work just fine. If Alice sends a letter with the word “green” and the messenger is captured, Eve won’t understand what Alice was saying to Bob (“Attack at dawn!”).

Good! What else can they try?

If they want to be more flexible in their communication, they need to find a better method. Namely, one that allows them to use the entire language. How can they write any message in a way that only they can read?

Well, what if they wrote the text in reverse? For example, “we are surrounded” becomes “dednuorrus era ew”. Does that work? At first glance this method also seems to do its job, although it doesn’t feel very secure. Can they do better?

What if Alice and Bob came up with their own alphabetic substitution rules? For example, they could write messages by substituting the letter ‘a’ with ‘d’, the letter ‘b’ with ‘k’, and so on. A full substitution rule might look like this:

Under this rule, the message “we are surrounded” becomes “yb dsb xtssatewbw”.

All these methods I’m proposing would be examples of cryptographic methods that fall under two major categories – codes and ciphers. Now let’s get back to the real world and take a closer look at each category.

Cryptography using codes

The color code system from the previous section is an example of a cryptographic code. When you use codes (as opposed to ciphers), you choose a set of symbols to represent some meaningful information. In the color example, the set of colors are the symbols and the sentences associated with them are the pieces of information.

In practice, the symbols are typically number or letter groups like 1104 or AADTR. And these symbols can represent information in the form of full words or sentences, syllables or other letter combinations, and so on.

Using cryptographic codes essentially requires inventing a new (private) language. In fact, to create a code you can even take a regular dictionary and come up with a new symbol for each word. Here’s how a part of such a code could look like:

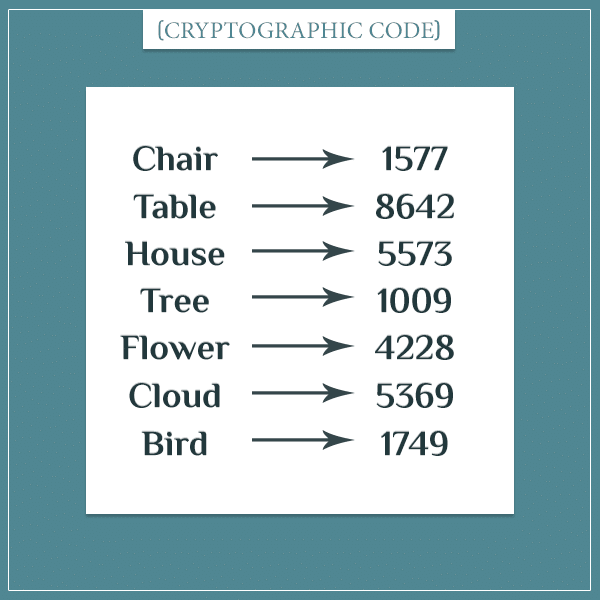
Using this code, you could write sentences in the form:

“… 1577 … 8642 … 5573.”

to mean something like “The chair and the table are in the house” (the … stand for missing words).

Of course, in order for this to work, all users of the code must be familiar with the meaning of each symbol. This is why a tool called a codebook is used. This is simply a place which stores all associations between symbols and information. It can be an actual book, an electronic device, or even the users’ memory.

An advantage of using codes is that they typically shorten messages. Also, if used properly, they can be difficult to crack, since the associations between symbols and meaning are random. On the other hand, an obvious disadvantage is that codes don’t allow for flexible communication. Meaning, you can only work with the available set of symbols in the codebook. Furthermore, the secure distribution of the codebook itself can become challenging by itself.

Cryptography using ciphers

Unlike codes, ciphers don’t operate at the level of meaning. Rather, they operate at the level of individual letters.

What ciphers do is take any text and somehow make it unreadable. In cryptographic literature, the original text is called the plaintext. Once it’s made unreadable, the result is called the corresponding ciphertext.

Do you remember the Alice and Bob examples from the beginning? Apart from the color code system, all remaining examples were using ciphers.

For example, in the text reversing method, “we are surrounded” is the plaintext and “dednuorrus era ew” is the ciphertext. And in the letter substitution method that same plaintext turns into the ciphertext “yb dsb xtssatewbw”.

Another important concept related to ciphers is a key. A key is a variable sequence of symbols or instructions that specifies the exact encipherment procedure of a particular message. Now, the two simple methods from the previous paragraph don’t have keys. And this makes them extremely insecure (practically unusable). You’ll see examples of cipher procedures with keys in the next posts when I introduce a few of the famous historical ciphers.

Transposition versus substitution ciphers

Ciphers roughly fall into 2 categories: transposition and substitution ciphers.

Transposition ciphers change the order of letters. For example, the text reversing method from the previous section is a transposition cipher. In that case, it changes the order of letters by reversing them. But in the general case, any algorithm that changes the letter order in some way is a transposition cipher.

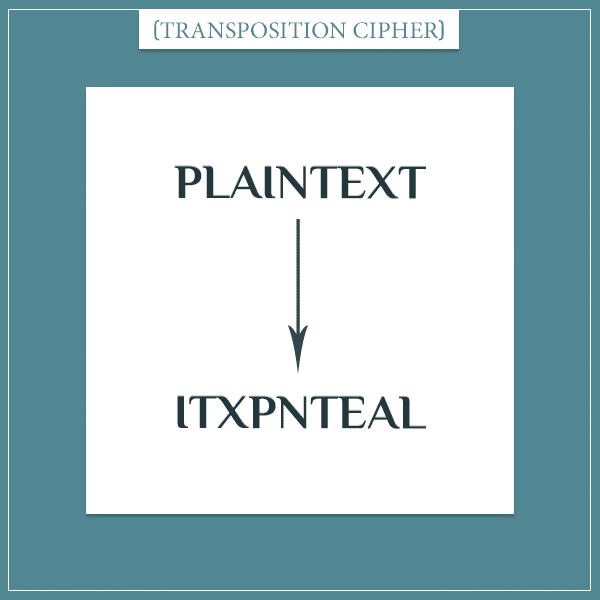
On the other hand, substitution ciphers leave the order of letters the same, but apply some algorithm that changes the letters to other letters.

The substitution rule above is an example of a substitution cipher.

In the posts to follow, I’m going to give real-world examples of both cipher types.

Monoalphabetic versus polyalphabetic substitution ciphers

Finally, I want to talk about a distinction that puts substitution ciphers into one of 2 categories: monoalphabetic and polyalphabetic ciphers.

In monoalphabetic substitution ciphers, each letter is substituted with the same letter throughout the entire message. The term comes from the Greek word “mono” which means “single”. The letter substitution rule above is a type of monoalphabetic substitution.

A weakness of monoalphabetic ciphers is that, once you learn the substitute of one cipher letter, you automatically know the true letter at every other position where that cipher letter occurs. For example, if you learn that the letter D in the ciphertext corresponds to the letter A in the plaintext in a single position, then you know that every other occurrence of D in the message is actually an A. This renders them rather insecure.

On the other hand, with a polyalphabetic substitution cipher a D in the ciphertext can translate to A in one position in a message, but to J in another position, to Z in yet another position, and so on. The Greek word “poly” means “many”, hence this class of ciphers employ “multiple alphabetic” substitutions throughout a single message. This makes them significantly more secure and difficult to crack.

In the next posts, you’re going to see real examples of both cipher types.

Summary

The intention of this introductory post was to give a high-level overview of cryptography and the important concepts from the field.

Cryptographic methods roughly fall under the categories of codes and ciphers. Ciphers themselves are two types: transposition and substitution ciphers. And substitution ciphers are classified as monoalphabetic and polyalphabetic.

• Cryptographic codes
• Cryptographic ciphers
  • Transposition ciphers
  • Substitution ciphers
    • Monoalphabetic ciphers
    • Polyalphabetic ciphers

Regarding ciphers, I also introduced the terms plaintext and ciphertext. And I also briefly mentioned the concept of a cipher’s key. You’ll see plenty of examples of those in the next posts.

Finally, I also talked about the combinatoric complexity of cryptographic methods and how it can be measured in terms of a method’s resistance to brute-force attacks.

I hope I managed to grab your attention and raise your curiosity about cryptography. Stay tuned for the next posts in the series!

---

Ready for part 2? Read about how people actually did cryptography in the ancient world!