Natural Numbers and Arithmetic: Intuition

Welcome to the third post from my series on numbers and arithmetic. In the previous two posts, I gave an overview of real numbers (and their main subsets), as well as the main operations between them. And in the rest of the series, we’re going to build all these concepts from scratch. Well, the focus in today’s post is the most basic subset of the real numbers: the natural numbers.

This post is part of my series Numbers, Arithmetic, and the Physical World.

In the introductory post, I talked about real numbers and their subsets consisting of the natural numbers, integers, rational numbers, and irrational numbers. I also gave an overview of the main arithmetic operations and their inverses:

• Addition – Subtraction
• Multiplication – Division
• Exponentiation – Roots/Logarithms

In the second post of this series, we looked at the most important properties of these operations. As a reminder, here are the main properties of single operations:

• Commutative
• Associative
• Identity element
• Inverse element

And here’s a table showing which operations have which of these properties:

I also talked about arithmetic properties of more than one operation. An important category is the distributive property of one operation over another. Here’s a table that summarizes the existing distributive properties (each row represents the operations over which the row’s operation distributes):

I also mentioned a few additional properties (both of single and multiple operations) and it’s probably good to go over the two previous posts if you’re not too familiar with this topic. Either way, the goal of this series is to get an intuitive understanding of all these properties.

Historically, natural numbers were the first discovered set of numbers. Then, with time, the other subsets of real numbers were built from natural numbers. For this reason, natural numbers are the best place to start our journey into the world of arithmetic. In today’s post, we’re going to focus on three main subtopics:

• The concept of a natural number
• The intuition behind operations with natural numbers
• Informal proofs of the properties of these operations

We’re going to temporarily set aside what we know and try to build this knowledge from the ground up. Kind of like mathematicians throughout history (although we will be taking many short-cuts).

Natural numbers

Alright, we don’t know anything about numbers yet, but we’re familiar with the fruit called ‘apple’ and its properties:

Apples are nutritious and tasty. We use them as a source of energy for our survival. So, we know that the picture above is different from this picture:

How are the two pictures different? Well, there are more apples in the second picture. And even more in this picture:

Even without knowing anything about numbers, we know that it matters if you have many apples, as opposed to few apples. If you have many, there’s more for you to eat or share with someone else (which means more nutrition). Soon we realize that it would be useful if we had a way of quantifying apples.

So, first we can come up with the somewhat vague concepts of “none”, “single”, “a few”, “many”, and so on. But at some point we realize that these concepts aren’t precise enough for all our purposes. We want to be able to keep track of exactly how many apples we’re dealing with. And this is when we reach the concept of counting. Counting is the first thing that should pop in your head when you hear natural numbers. Because the primary function of natural numbers is to keep track of counts of things.

Building the set of natural numbers

Among the vaguer concepts above, the first is still precise enough. The concept of “none” just means no objects (of whatever kind). We can then define our very first number that represents this idea: zero. To apply it to our apples example, if you have an empty basket, this means you have zero apples. The other concept which is also precise is that of a “single” object. We decide to define another number to represent this: one. If you have a basket with a single apple in it, this means you have one apple.

So far, so good. We have our first two precise numbers. And it turns out that from these two we can derive all other numbers! We do this using the simple idea of adding one object to an already existing group of objects.

If you have a basket with zero apples and add one apple to it, you get a basket with one apple. Then, if you add another apple, you get a basket of… How should we call it? How about: two apples. Then if we add another one, we get three apples. Then four, five, six…

Nothing is stopping us from continuing this indefinitely. Each addition of a new single apple leads to a count represented by the next number. And, just like that, we defined the full set of natural numbers!

Intermezzo: Is zero really a natural number?

Before we continue, I just wanted to quickly mention that today there are two different conventions when it comes to the number zero. Some mathematicians prefer to treat natural numbers as starting from one and therefore exclude zero from the set. And, in fact, historically the concept for “zero” emerged a little after the concept for counting numbers.

I personally prefer the convention that does treat zero as a natural number, but there are solid arguments for both conventions. I also think that accepting one convention over the other doesn’t make a big difference and, at least in my mind, this isn’t a debate worth spending too much time on.

In this post (and the rest of the series) we’re going to use the convention that does treat zero as a natural number.

Symbolic representation of natural numbers

So far, we only have words like “zero” and “one” to represent numbers. But even though they have a starting point (zero), natural numbers don’t have an ending point. Which means if we were to invent a new word for every number, we would need to keep inventing words indefinitely. Not to mention the difficulty in having to memorize all these new words. What we need is an efficient and consistent way of representing numbers, both in written and spoken language.

For example, we could use tallying to represent counts. Every time we add a new apple to the basket, we draw a single vertical line on some surface.

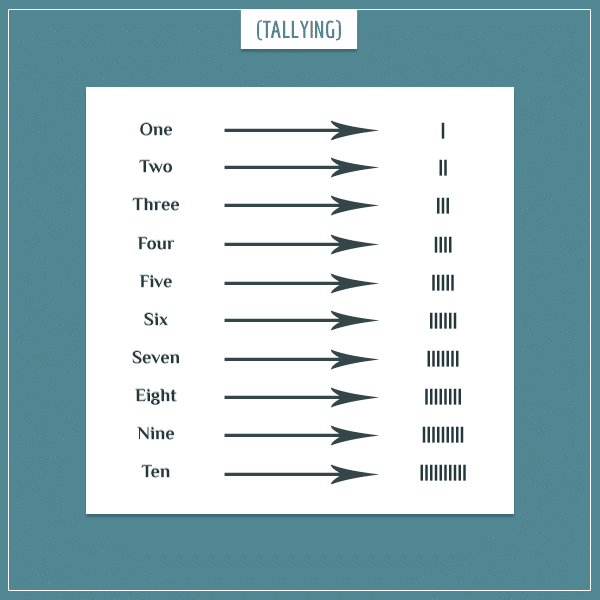
In fact, this is exactly what early humans did in Africa starting over 30 000 years ago. They would scratch lines on things like wood or animal bones to represent the count of different types of objects. Tallying evolved throughout the centuries into more sophisticated versions but it was still not the most efficient way of representing numbers.

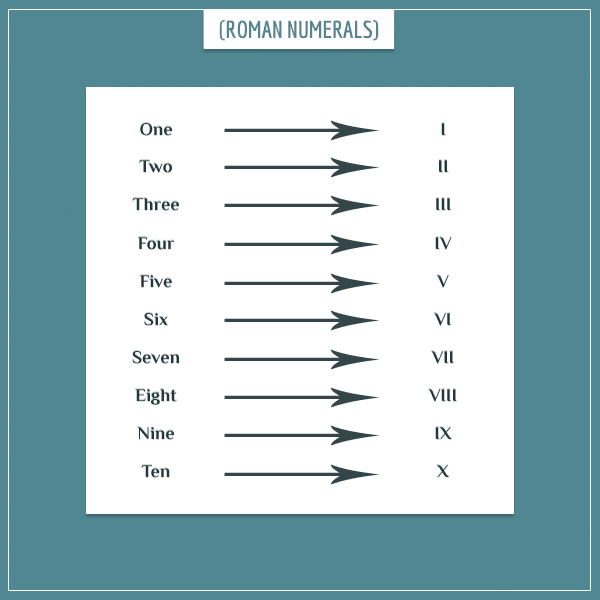
Better ways began emerging in the last 10 centuries BCE in places like China, Ancient Greece, and the Roman Republic. Today, we call all these different representations numeral systems. Numerals themselves are the symbols used for representing numbers. One of the famous ones from that period (which is still in use) is the Roman numeral system which used the Latin alphabet to represent numbers:

Fast forward to the period 7th to 9th centuries CE, during which the most commonly used numeral system today was invented in India and spread around the world by the Arabs: the Arabic numeral system we’re all familiar with.

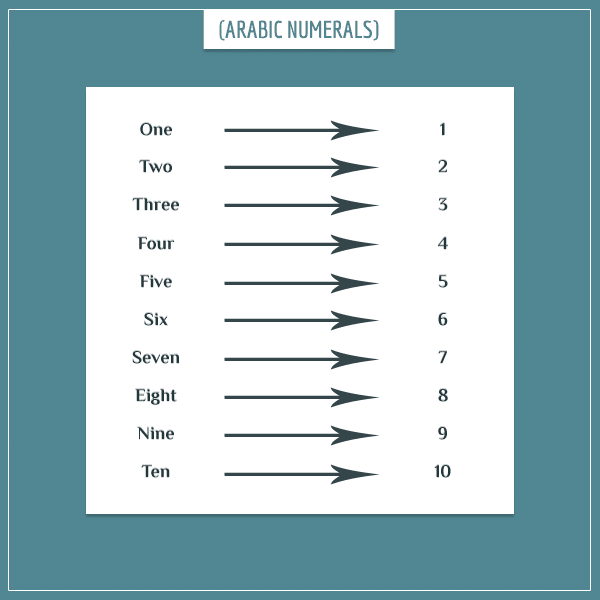
Even though the topic of numeral systems is interesting in its own right, I don’t want to go into too much detail here. I just want to draw your attention to the distinction between numbers and numerals and emphasize that there are many ways to represent a number. Anyway, for this post let’s stick with what we’re most familiar with and represent numbers with the Arabic numeral system.

If you’d like to learn more about the topic of representing numbers, check out my post dedicated to numeral systems.

Operations with natural numbers

Alright, now that we have a concept for natural numbers, let’s look at the arithmetic operations we can perform with them. I’m going to go over the operations in a particular order that I think is most intuitive. In a way, all these operations relate to each other because either they’re derived from each other they’re each other’s inverses.

Many of you are probably already familiar with the technical details of these operations, so I want to focus on their intuition instead. But still, for those of you who are completely new to the field (or if you just need a refresher), I’m going to include a few videos in each section. Most of these videos are from Khan Academy, a website I strongly recommend in general if you need a refresher on any mathematical topic. The author Sal Khan is an amazing instructor who can help you with many topics, not even limited to mathematics alone.

Nowadays, you can easily perform these operations between any two numbers using calculators and you’ll rarely find yourself in a situation where you actually have to perform them manually. Still, the techniques for performing them manually are useful to get an even better intuition about the operations.

Addition and multiplication

Addition is the simplest operation to define. In fact, we kind of did already, when we were defining the concept of “the next natural number” by adding 1 apple to a basket that already has some fixed number of apples in it. If we go back to tallying, we can represent addition by drawing a vertical line after each apple we add to the basket.

So, if we have a basket with a single apple in it, our initial state is a single vertical line. If we we have another basket with 3 apples in it and decide to move them to the first basket, we would add 3 vertical lines to the existing one to get 4 apples. Here’s the modern mathematical notation for this operation:

   

The “plus” (+) and “equals” (=) signs themselves were invented around the 14th and 16th centuries, respectively. The convention for + is that you’re adding the numbers to the left and to the right of the sign. Similarly, the convention for = is to express that the numbers on its two sides are the same number. The term for the number to the right of = is the sum of the two numbers.

Anyway, this is all that addition of natural numbers is. Pretty simple. And this operation is probably as close as you can get to directly relating math to the real world.

Now let’s consider our first level of abstraction. Suppose we’re adding the same number multiple times. For example, let’s add the number 2 four times:

   

Since we’re adding the same number, instead of repeating it, can’t we try to come up with some sort of a short-cut notation? Well, we can. And it’s how people first reached the concept of multiplication:

   

The “times” () sign is one of the most common notations for multiplication. The number to the right of the sign is the number we’re adding multiple times and it’s called the multiplicand. And the number to the left is how many times we’re adding it, called the multiplier. An alternative notation which is even more common (and which we’re going to stick to) is the “dot” sign:

   

The term for the number to the right of = is the product of the two numbers.

Techniques for performing addition and multiplication

When we’re dealing with large numbers, adding or multiplying them with tallying is more than impractical. Luckily, there are ways to perform these operations with arbitrarily large numbers in almost no time.

Here’s a short video in which Sal solves an example with adding two large numbers:

And here’s another video in which he solves a few multiplication examples of 2- and 3-digit numbers.

Subtraction and division

Subtraction and division are the inverse operations of addition and multiplication, respectively.

Like addition is about adding objects, subtraction is about taking away objects. For example, if you already have 4 apples and somebody takes 3 of them, you will end up with 1. We express this operation with the “minus” (–) sign (this notation was adopted around the 15th century):

   

We can perform this operation with tallying as well. For example, if you already have 4 vertical lines representing the 4 apples, you can scratch 3 of them in the middle to represent that 3 have been subtracted. Then you will end up with a single unscratched vertical line that represents the result of the operation.

One thing to be careful about here is that, unlike addition, subtraction is defined only if the number being subtracted is less than or equal to the number you’re subtracting from. That is, once you reach 0, you can’t take away anymore. Remember, we’re in the world of natural numbers!

The term for the number to the right of = is the difference of the two numbers.

Similarly, division is the opposite of multiplication. Remember how multiplication is nothing but repeated addition?

   

Well, division is simply answering the inverse question. Namely, if we have 8 apples and we split them into groups of 2, how many groups will we have? A common notation for division is the “division” sign ():

   

The number being divided (to the left of the sign) is called the dividend, whereas the number we’re dividing by (to the right of the sign) is called the divisor. This sign was first used around the 17th century but today a much more preferred notation is to simply separate the dividend and the divisor by a horizontal line (which is also the notation we’re going to stick with):

   

The term for the number to the right of = is the quotient of the two numbers.

When is division defined for natural numbers?

Like subtraction, division is only defined if the divisor is less than or equal to the dividend. At least in the realm of natural numbers. Also, not all divisors work for a particular dividend. For example, you can’t divide 7 objects into groups of 2.

Although there is a way out, with the help of the concept of the remainder of a division operation. This is the amount that is “left over” after we’ve distributed as much as we can from the number into groups of a particular size. For example, if we try to divide 7 into groups of size 2, we could express this as:

   

The last group contains a single object, so dividing 7 by 2 gives us 3 with a remainder of 1. On the other hand, if all groups contain exactly 2 numbers (like when the dividend is 8), we simply say that the remainder is 0. Another way to say it is that 8 divides evenly into 2.

With remainders, we can even define division when the dividend is less than the divisor. Then the quotient will simply be 0 with a remainder equal to the dividend. For example, 2 divided by 3 is equal to 0 with a remainder of 2. You can learn much more about division with remainders in my post dedicated to the topic of Euclidean division.

Finally, division by the number 0 is always undefined and it’s easy to see why. Say you’re trying to divide 8 by 0. How many times should we add 0 to itself to get 8? Well, it wouldn’t work, because no matter how many times you add it, the result will always remain 0.

Techniques for performing subtraction and division

Like with addition and multiplication, we need to have methods for performing subtraction and division fast, even with very large numbers.

Here’s another video by Sal in which he demonstrates the technique for subtraction:

And another one with a few division examples, both with and without remainder:

Notice how to multiply two numbers we only need to know about addition but when we’re performing division, we need to have addition, subtraction, and multiplication in our toolkit.

Exponentiation

Remember how we defined multiplication as an abstraction over addition? I told you that you can view multiplication as a short-cut notation for adding the same number many times. But what is to stop us from doing the same for multiplication itself? That is, can’t we also have a notation for multiplying the same number many times? For example:

   

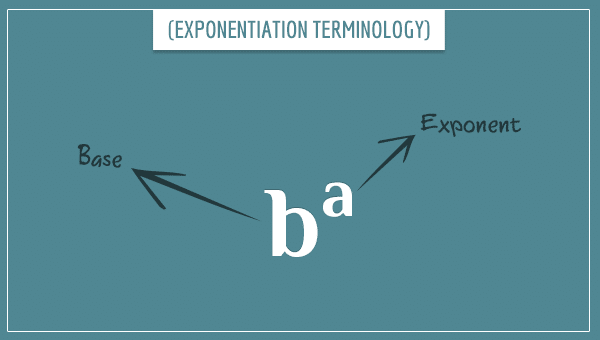
Well yes, we can! This is the arithmetic operation called exponentiation for which the most common notation is to write the number of times we’re multiplying a number at the top right corner of the number itself:

   

Remember the terminology? We read the left-hand side in the above expression as “2 (raised) to the power of 4”, where 2 is the base and 4 is the exponent:

Well, like I said, this is yet another level of abstraction. If we didn’t have exponentiation in our bucket of arithmetic operations, we would have to write as . And if we didn’t have multiplication either, we would have to write it as . Kind of wasteful, yeah?

Still, remember that exponentiation ultimately boils down to repeated addition. From this we can also see why 0 raised to any power is always equal to 0. The case for raising a number the power of 0 is an interesting one, however.

Raising a natural number to the power of 0

What is 2 to the power of 0 ()? Your first instinct might be to say that it should be equal to 0, but that’s not how it is. Actually, raising any number to the power of 0 is equal to 1. Let me try to give you the intuition.

First, let’s go back to multiplication for a moment. We said it’s just a short-cut notation for adding the same number many times, right? And we write this as:

   

But you can actually also represent this as:

   

That is, we can think of multiplication as sort of an instruction as to how many times to add the number to the right of the sign to 0. With this convention, we also see why any number multiplied by 0 is equal to zero — whatever the number is, we add it to 0 zero times, so the final result remains 0. Similarly, multiplying 0 by any number equals 0 because we will just be adding a bunch of 0’s to 0.

By analogy, we can represent repeated multiplication as the number of times we multiply the number 1 by the base of the operation:

   

Which means that if we raise any power to 0, we simply won’t touch the 1 (won’t multiply it by the base at all) and the result will remain 1. Thus, for all a:

   

By this logic, should also be equal to 1, right? This is, in fact, the most common convention in mathematics. But still, there’s a small conflict, since we also know that 0 raised to any number is equal to 0. For this reason, some fields choose to treat this expression as undefined. In rare cases, I’ve even seen a convention for (where the context makes this more suitable).

By the way, if you’re wondering why we used 0 for repeated addition but 1 for repeated multiplication… Well, this is because 0 and 1 are the identity elements of the two operations. In a way, we are representing multiplication and exponentiation as repeated application of their underlying operations (addition and multiplication) on the respective identity elements. Why? Because the identity element is the number which leaves any other number unchanged when the operation is applied on both.

You remember identity elements from the previous post, right? We’re about to revisit this topic soon anyway.

Roots and logarithms

Unlike addition and multiplication, exponentiation has two inverse operations. Like I explained in the introductory post, this is because there is an inherent asymmetry between the numbers to which the operation is applied.

Roots are the answer to the question: “Which base should I raise to a particular exponent, in order to get a particular number?”. The notation for this operation is the “radical” sign (√) where the exponent is written in the top left corner and the number whose root we’re taking inside the sign:

   

The above example represents the 3rd root of 8, which is equal to 2 (because 2 raised to the 3rd power is equal to 8).

Logarithms answer the opposite question: “To which power should I raise a particular base, in order to get a particular number?”. The notation here is the abbreviation log, followed by the base in the bottom right corner and the number itself:

   

You can read the right-hand side as the base-2 logarithm of 8. Which is equal to 3 because 2 to the power of 3 is 8.

With natural numbers, most of the time you can find roots and logarithms by simple guess work. For example, when trying to find the 3rd root of 8, we can try raising 0 to the 3rd power (to get 0), 1 (to get 1), 2 (to get 8)… Bingo! And logarithms are even easier. You just keep multiplying the base to itself until you get the desired number — the number of times you did the multiplication is the answer you’re looking for.

There are more direct techniques for solving roots and logarithms but they are more involved and, in my opinion, not really worth the effort when we know we’re only dealing with natural numbers. I’m going to mention these techniques in the next posts of the series when we start applying these operations on more general number sets.

When are roots and logarithms defined?

As you can probably guess, these two operations won’t work with all pairs of natural numbers. For example, an expression like is undefined because no natural number raised to the 4th power results in 9. Similarly, an expression like is also undefined because there’s no power to raise 3 to that will give us 7. When we begin looking at other subsets of real numbers, you’ll see that these operations will gain meaning and will no longer be undefined. But, in the world of natural numbers we have to treat them as such.

Other than that, there’s two special numbers to be careful about with these operations: 0 and 1.

First, 0 cannot be the exponent in a root operation because any number raised to the power of 0 is equal to 1. Which means there’s no way to get the number under the radical sign, regardless of which number you try to raise to 0.

Second, the base of a logarithm cannot be 0 or 1, since there is no power to which you can raise these numbers to obtain anything other than 0 or 1. Finally, the number whose logarithm is taken can’t be 0 since there’s no exponent that can turn a base into 0.

Properties of operations with natural numbers (informal proofs)

So far we explored the concept of natural numbers and the most important operations we can perform with them. And in this final section I want to give you some intuition about the properties of these operations.

I’m going to give informal and intuitive proofs for why these properties exist. Until the 19th century, mathematicians were more or less relying on such intuitive proofs for these properties. Since then, all existing properties have been proved formally as well, thanks to the work of great mathematicians like Richard Dedekind, Charles Sanders Peirce, and Giuseppe Peano. In particular, the last of these mathematicians is responsible for the proper axiomatization of natural numbers. The set of axioms are naturally named after him and are called the Peano axioms.

I’m only mentioning these axioms here and I don’t want to go into any details yet. Just know that they exist and all properties we’re about to prove informally can also be proved formally, starting from the Peano axioms. But in this series we’re mainly concerned with the intuitive relationship between mathematical and real-world objects, so let’s leave the axiomatic approach for a future post.

Anyway, here we’re going to look at most arithmetic properties from the previous post, both of single and two operations. I say most because some of these properties can only be defined after we have first defined integers and rational numbers (for example, the inverse element property).

The commutative property

In the previous post we learned that the commutative property holds only for addition and multiplication and for none of the other operations we’re considering in this series. Which means that for any two natural numbers a and b, the following equalities hold:

   

   

The commutative property of addition is very intuitive and easy to demonstrate. Say you have 3 green apples and 2 red apples:

The commutative property simply states that if you put these two sets of apples next to each other, it doesn’t really matter if you put the red apples to the left or to the right of the green apples. In both cases, when you count them, you’re going to get the number 5:

Pretty simple.

On the other hand, the commutative property of multiplication isn’t as obvious. It’s telling us that, for example, is the same as . That is, adding the number 3 two times is the same as adding the number 2 three times:

   

We can manually check that it will work for this particular example, but how can we assure ourselves that it will always work? Well, let’s try to gain some intuition about this with some more apples. We can represent as 2 rows of 3 apples:

Let’s see what happens if we simply rotate this group of 6 apples 90 degrees, without touching their positions relative to each other:

Notice how after the rotation the number of rows becomes 3 and the number of apples in each row becomes 2. Therefore, we can think of the above image as representing the operation .

You can see why this will generally work exactly the same with any two natural numbers, right? When you group the objects into rows and columns and rotate them 90 degrees, the number of columns becomes equal to the number of rows prior to the rotation, and vice versa. But the rotation itself doesn’t change the count of the objects.

Why aren’t the other operations commutative?

In principle, to prove that a property doesn’t hold, you need to show one example where the property doesn’t hold. That’s because a property is supposed to hold for all numbers for which the operation is defined and a single counter-example is sufficient to demonstrate that this is not the case.

Still, it’s good to have some basic intuition about why a property doesn’t work. Take subtraction for example. The property only works in the case where you’re subtracting a number from itself. Another way to say this is that, under subtraction, every number commutes with itself. But if the numbers are different, by definition one will be larger than the other. And it definitely matters if you’re subtracting the smaller number from the larger one or the other way around. Well, subtracting the larger from the smaller number isn’t even defined with natural numbers.

The same reasoning can be applied to division. Every number commutes with itself, but if the numbers are different, it matters if you’re dividing the larger by the smaller or the other way around.

What about exponentiation?

The case for exponentiation is somewhat more interesting. In the previous post we learned that it’s not commutative and there’s countless examples to demonstrate this (e.g. ). Because it’s not commutative, there’s no reason to expect that its inverses (roots and logarithms) would be commutative either (which they aren’t). But why isn’t exponentiation itself commutative, like the other “positive” operations?

The short answer is that not all properties of an operation are guaranteed to be preserved when we generalize it. In a way, we’re kind of lucky that addition and multiplication are commutative. If you try to define some random binary operations, chances of them turning out to be commutative are actually rather small. And for the case of exponentiation, the commutative property simply doesn’t happen to hold.

Still, to get some intuition about why it doesn’t hold, let’s try to give a real-world interpretation of the effects of exponentiation. Take an expression like . We already know we can represent this multiplication as 3 rows of 3 apples each:

On the other hand, how would we represent the operation if we switched the places of the base and the exponent? That is, how would we represent an expression like ? Well, we start with a row of 2 apples and multiply it by 2 to get 2 rows of 2 apples. Then, we multiply all that by 2 again, which is like stacking two apple squares next to each other. Which gives us a cube:

Regardless of how you try to rotate or flip the square (representing ) you will not be able to get it into the form of the cube (representing ) because the two are different objects with different structures.

In other words, the base and exponent serve different roles in the operation. In a way, the exponent determines the number of dimensions of the resulting object, whereas the base determines the size of the dimensions.

The associative property

In the previous post we learned that the associative property also holds only for addition and multiplication. The informal proofs here are equally intuitive.

We can demonstrate the associative property of addition with apples in the following way. Imagine we start with 3 green, 2 red, and 2 yellow apples:

Now let’s try to represent adding these three rows. Mathematically, we express this as and the associative property tells us that:

   

Why does the property work? Well, we can think of as first adding the red and yellow apples and then adding the resulting group to the green apples:

And we can represent as first adding the red apples to the green apples and then adding the yellow apples to the resulting group:

In both cases, we’re adding the same number of apples together and the order in which we do it doesn’t change the final count.

The associative property of multiplication is a little trickier to demonstrate, but it’s still pretty intuitive. Let’s start with an expression to work with, say . The associative property tells us that:

   

To prove that it’s true, let’s first rewrite the two expressions with parentheses in the following way:

   

   

Notice that we know we can rewrite them like this because all we did was to switch the places of numbers by applying the commutative property (which we already proved). Therefore, proving the associative property boils down to showing that:

   

Now let’s focus on the parts inside the parentheses: and . We can think of this as having a row of 3 apples that we’re going to multiply 4 times or 2 times:

Once we multiply this row by 4 or 2, then the full expression tells us that we need to multiply the resulting rows by the number outside the parentheses. Therefore, is telling us to first multiply the row by 4 and then by 2, whereas is telling us to first multiply it by 2 and then by 4. But, by the commutative property of multiplication, we know that this order doesn’t matter and in both cases we’re going to end up multiplying it by .

And from this we can conclude that the equation should be true. And by extension the equation as well. Generally, this will work for any three numbers a, b, and, c.

Why aren’t the other operations associative?

To see why subtraction isn’t associative, let’s consider the two example expressions:

   

   

Notice how in both cases you end up subtracting something from the first number (6). In the first case, you first subtract the third number from the second number (4 – 1) and then subtract this difference from the first number (6). However, in the second case, you subtract the whole second number from the first (6 – 4) and then, on top of that, you also subtract the third number (1). Regardless of what the numbers are, you’re going to subtract more in the second scenario than in the first.

The situation with division is analogous. Take the expressions:

   

   

Again, in both cases we end up dividing the first number by something. But in the first case we’re dividing it by the result of the division of the other two numbers, whereas in the second we’re successively dividing it by each number. So, whatever the numbers are, you’re bound to obtain a different final result.

The reason exponentiation isn’t associative (as well as its inverses) is the same as the reason why it isn’t commutative. Namely, the base and the exponent serve different roles in the operation. Therefore, we should expect an expression like to be completely different from an expression like . This is because and have different bases and exponents (as will be the case most of the time).

Identity elements

The identity element properties of addition and multiplication are very simple and intuitive. As you know from the previous post, 0 is the identity element of addition and 1 is the identity element of multiplication. As a reminder, the identity element of an operation is a number that leaves all other numbers unchanged, when applied as the left or the right number in the operation. This means that, for any natural number a:

   

   

For addition, if you don’t add any apples to an existing group, the number of apples won’t change. Similarly, if you multiply a row of apples by 1, you still get the same row.

On the other hand, subtraction, division, exponentiation, and roots only have right identity elements. For subtraction this is the number 0 and for the other three operations it’s the number 1.

As an exercise, try to intuitively explain why these operations don’t have a left identity element and why logarithms don’t have an identity element on either side.

Distributive properties

Now that we covered the properties of single operations, it’s time to take a look at the distributive properties of an operation over another. In the previous post I told you that multiplication distributes over addition both on the left and on the right. Which means, for arbitrary numbers a, b, and c:

   

   

The other distributive properties are:

• multiplication over subtraction (left and right)
• division over addition and subtraction (right only)
• exponentiation over multiplication and division (right only)
• roots over multiplication and division (right only)

It shouldn’t be too surprising that division, exponentiation, and roots don’t have any two-sided distributive properties. This is due to them not being commutative. Do you see why their non-commutative nature wouldn’t allow them to distribute on both sides over any operation?

In this post I’m going to exclusively focus on the distributive property of multiplication over addition and leave the discussion on the remaining properties for the next posts in the series. There are some caveats regarding some of them and the explanations will make more sense when we’re already familiar with some of the other number sets.

As a matter of fact, the distributive property of multiplication over addition is the most important distributive property, as will become clear by the end of the series.

By the way, as an exercise, try to see for yourself why none of the other distributive properties hold on the left or on the right.

Multiplication distributes over addition (intuition)

Let’s take the expression and work with it to see why this distributive property holds. First, we know that:

   

Now, let’s take the left-hand side and split it in two parts of length 3 and 2 using the associative property of addition:

   

Now we can rewrite the right-hand side of this equation as the sum of two products:

   

And, combining this with the first equation, we see that:

   

Finally, notice we can write 5 as (3 + 2):

   

And, just like that, we obtained the right distributive property! The left distributive property has the same intuition, but it also directly follows from the commutative properties of addition and multiplication.

In this case the numbers happen to be a = 2, b = 3, and c = 2. But you see how this would work out exactly the same with any other numbers. Here’s some visual intuition with apples:

The above image represents the operation which we can also write as . And if we split the numbers with an imaginary line, we can interpret it as representing as well.

Special exponential and logarithmic properties

To conclude this post, I want to give you some intuition about two important properties of exponentiation and logarithms. I’m not going to cover all special properties from the previous post and leave some of them for the next posts of the series, since they only become relevant in the context of more general number sets.

The two exponential properties that we’re going to look at are:

   

   

And the logarithmic properties we’re going to look at are:

   

   

As you’re about to see, these two sets of properties are actually very much related.

The exponential properties

Alright, let’s start with the property which is telling us that raising any number (a) to the sum of two numbers (b and c) is the same as the product of a raised to b and a raised to c. We can derive this property in a very similar way to how we derived the distributive property of multiplication over addition.

Let’s take the expression and split it in two parts using the associative property of multiplication:

   

Now we can rewrite the right-hand side as the product of two powers:

   

Combining the two right-hand sides, we get:

   

Basically, the idea is that we can split any exponent into a sum of two smaller numbers, just like we can split the repeated multiplication into two groups whose size is equal to the same numbers.

Now let’s look at the second property which is very similar. Let’s take an example expression like and rewrite the inner exponentiation as repeated multiplication:

   

Now let’s expand the second power too:

   

If we count the number of 3’s in the final result, we see that it’s precisely , which is nothing but the product of the two powers. And it’s intuitive to see that the same would hold true for any other combination of powers.

The logarithmic properties

The logarithmic properties we want to prove are:

   

   

Like I said, these two properties basically follow from the two exponential properties above. I’m only going to prove the second one and leave the first one as an exercise for you. And this time (as a conclusion to the post) I’m going to prove it a little more rigorously, instead of using examples with concrete numbers.

So, the property says that if the argument of a logarithm is raised to some power, this is the same as multiplying the logarithm of the argument by that power.

First, let’s set the left-hand side equal to some unknown value x:

   

Remember, the logarithm is the answer to the question “to which power should I raise the base, in order to obtain the argument?”. In this case, the base is a, so we’re looking for a value for x such that:

   

Now let’s consider a simpler expression where the argument isn’t raised to a power and set it equal to another unknown value y:

   

Which we can rewrite as:

   

Now let’s raise both sides of the last equation to the power of c:

   

Notice that both and are equal to which means they are equal to each other:

   

Using the second special exponential property and the commutative property of multiplication, here we can rewrite the right-hand side as:

   

From which we conclude that:

   

Finally, we substitute the values of x and y with the initial logarithms we started with to obtain:

   

Simple, right?

Summary

Even though this ended up being a pretty long post, I hope it was straightforward to follow.

We basically derived the concept of natural numbers from the mere act of counting objects. The number 0 represents no objects at all and the number 1 represents a single object. From that point on, we can derive each successive natural number by continually adding 1 object to a group of objects: 0, 1, 2, 3, 4, 5, …

I also told you that it’s important to distinguish between a number itself and its symbolic representation, called a numeral. The number four is the number four, regardless of whether you represent it as ||||, IV, 4, or using any other numeral system.

We also defined the “positive” operations addition, multiplication, and exponentiation, as well as their respective inverses subtraction, division, roots, and logarithms. As we first learned in the previous post of this series, some of these operations happen to have certain properties. Namely, the commutative, associative, and identity element properties of single operations, as well as the distributive property of multiplication over addition and a few special exponential and logarithmic properties. In this post, I showed you the intuition for why these properties hold in the world of natural numbers.

As always, feel free to ask any questions or leave feedback in the comment section below. I’ll see you in the next post on negative numbers and integers where we’ll extend our notion of numbers into a more general set.