Negative Numbers and Arithmetic: Intuition

Many numbers of different sizes with the planet Earth in the background and the text "negative numbers" in the foreground

Hi everyone, and welcome to the next post from our journey in the world of numbers. Where we last left off, I was telling you about natural numbers — the objects that most naturally appear when we make our first steps in the world of Mathematics. Well, today’s post is about the next most natural kind of mathematical objects: negative numbers and the new structure they form together with natural numbers called integers!

This post is part of my series Numbers, Arithmetic, and the Physical World.

In the previous post, I related our discovery of natural numbers to the need to count (or order) objects from the physical world we interact with. We want to be able to distinguish between different quantities in a precise manner, not just vaguely with terms like “few” and “many”. So, we came up with different systems to represent things like “three apples”, “a hundred people”, or “the twenty-fifth day of the month”.

Once we got comfortable with numbers, we gradually developed operations we can perform on them. For example, we learned to mathematically describe the process of adding together two or more groups of objects, each with potentially different counts. Then we generalized this operation for the case of adding the same number multiple times to arrive at the idea of multiplication. Then we generalized that too to the idea of exponentiation, which is multiplying by the same number multiple times. Finally, we started studying the properties of those operations and discovered their inverses as well, in the form of subtraction, division, and taking roots and logarithms.

Table of Contents

Why didn’t we stop at natural numbers?

So far everything sounds cool. We know how to take any two numbers and add them together:

$4 + 8 = 12$

We can also take any two numbers and multiply them:

$2 \cdot 13 = 26$

And nothing’s stopping us from taking any two numbers and raising one to the power of the other:

$3^4 = 81$

Of course, apart from these examples, we can substitute the concrete numbers above with any pair of natural numbers a and b and all expressions that look like $a + b$

, $a \cdot b$

, and $a^b$

will be perfectly valid. That is, the result will always be another natural number.

Then we can also take any two natural numbers and apply all inverse operations on them… Or can we? See, this is where we encounter a problem. Like I showed you in the previous post from this series, subtraction, division, roots, and logarithms aren’t defined for all pairs of natural numbers. In fact, it turns out they aren’t defined for most pairs!

Well, today we’re going to exclusively focus on solving the problem with subtraction. Take a look at this example:

$4 - 6 = ?$

Here we’re basically asking “Which number do I add to 6 in order to get 4?”. But there is no such natural number! Anything you add to 6 will produce a number greater than or equal to 6, there’s no way you’re getting anything smaller. If the operation was $6 - 4$

instead, then we wouldn’t have a problem answering this question. The number we need to add to 4 to get 6 is 2 and there’s nothing more to it.

But it’s rather uncomfortable that we can’t subtract a number from a smaller number, isn’t it? To just leave things “undefined” like that… Why don’t we try to make this operation defined for all pairs of numbers somehow? Of course, we want to do it in a way that leaves the original definition intact.

The need for a new kind of number

We want our extended definition of subtraction to preserve all properties of the operation. Furthermore, we want to be able to use the result of the operation just like we do with other numbers. We don’t want to just come up with a random definition that isn’t consistent with what we’ve discovered so far, right?

Well, we just saw that for any pair of natural numbers a and b, where $a < b$ , there is no natural number c such that $a - b = c$ . This means that c has to be some other kind of number. To get a better intuition for what this new kind should look like, let’s review what subtraction is actually doing. Let’s start with visualizing the natural numbers as they appear in their natural order:

To add two numbers, like 2 and 3, you start at the first number and make a number of steps to the right equal to the second number. That is, start at 2 and make 3 steps to the right. The number you end up on is the result of the operation:

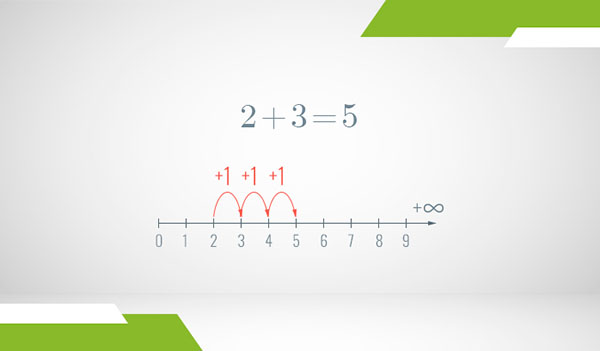
A number line of the positive integers where addition is illustrated as steps with arrows

Subtraction works exactly the same way, except we make the steps to the left:

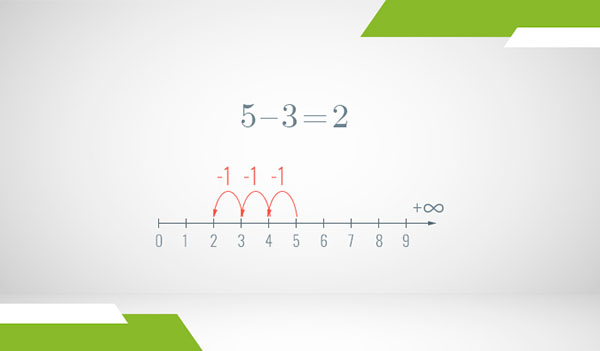
A number line of the positive integers where subtraction is illustrated as steps with arrows

As expected, when we start from the sum of two numbers and subtract one of the numbers from it, we end up on the second number (subtraction being the inverse operation of addition and all). If we subtract 3 from 5, we end up at 2 because 3 + 2 = 5. Similarly, if we subtract 2 from 5, we end up at 3:

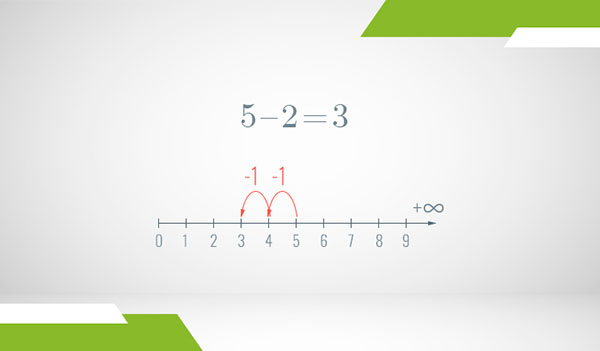
The “birth” of negative numbers

So far, so good. Now, in this setting, what is the problem if the number we’re subtracting is larger than the number we’re subtracting from? Let’s go back to the earlier example of $4 - 6$ . We are instructed to start at 4 and make 6 steps to the left. But the first 4 steps already take us to the number 0, which is the first natural number and there’s no more “to the left” to go!

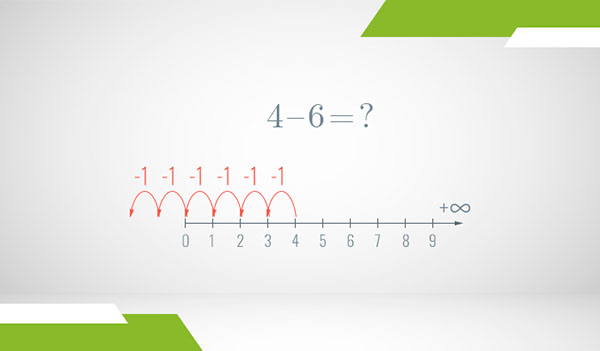
So, here’s where we decide to push our boundaries. What if the natural numbers weren’t the full picture and the actual set of numbers extended infinitely to the left, as it does to the right? That is, what if the true number line looked something like this instead?

A number line of the integers (negative ones not labeled)

If that’s the case, then $4 - 6$ means we simply need to make 4 steps to the left to reach 0 and then 2 additional steps to the left:

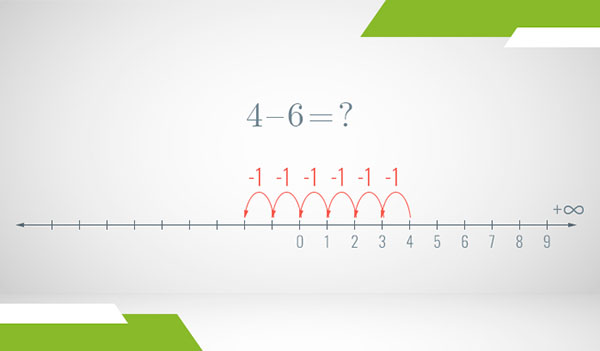
Look at that, seems like we might have just reached a completely new place in the world of Mathematics! Let’s explore it and see what we find.

The first step is to come up with a way to represent these new numbers with the same terms as we represent natural numbers. Well, since where we ended up is exactly 2 steps to the left of 0, why not call that number “minus 2” or simply -2? We came to this choice because it’s the “minus” operation that took us there. And while we’re at it, let’s apply the same logic to the remaining unnamed numbers:

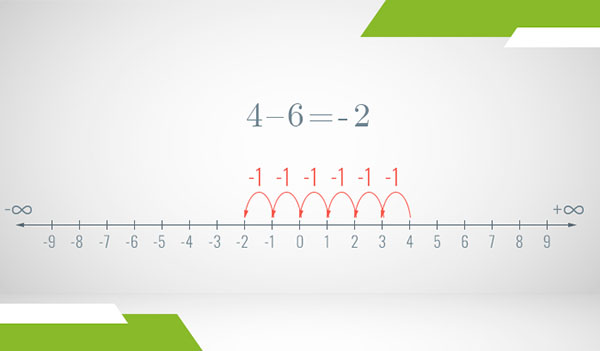
A number line of the integers where subtraction is illustrated as steps with arrows

It turns out we just discovered negative numbers!

What do negative numbers represent?

It seems like we made a genuine new mathematical discovery but let’s make sure it really is a coherent concept. In this section I want to give some basic intuition about negative numbers. And in the rest of the post I’m going to focus on how the familiar operations work with them.

So, natural numbers had a natural interpretation as counts of things, right? That is, the real-world concept that corresponds to natural numbers is “quantity of objects”. For example, the number 3 can represent the count of the this row of apples:

Now let’s try to build a similar intuition about negative numbers by relating them to something we’re familiar with.

Imagine you have 0 apples but you really feel like eating one. So you ask to borrow an apple from your friend, promising to give back another apple tomorrow. Right after you eat the borrowed apple, you still have 0 apples on you, but can we really say you possess 0 apples? If that were the case, it would mean that when you get an apple tomorrow you will have 1 apple. But remember, tomorrow you also have to give an apple back to your friend, so you’ll still be left with 0 apples.

Then what is the state of your “apple account” after you ate the apple you borrowed? Well, it seems like “negative 1” or simply -1 is a really appropriate candidate, don’t you think? Because however many apples you obtain tomorrow, you know you’re going to have to subtract 1 from them to return the borrowed apple to your friend.

Now I want to introduce you to a metaphorical object I’m going to use for representing such “negative” quantities. Meet the anti-apple!

Artistic depiction of a hypothetical "anti-apple" (a "negative apple")

Anti-stuff

We’re already familiar with many things that are “opposites” of each other, right?

cold versus hot
big versus small
good versus evil

…and so on. What all these dichotomies have in common is that they describe things that (may) have identical properties, except for one property on which they are opposites. In general, at least in English, you can create the “anti” of something by simply attaching the word “not” before it, even if there is no special word to describe its opposite. For example, “blue” versus “not blue”, “overwhelmed” versus “not overwhelmed”, and so on.

In many sciences we have objects which are natural opposites of each other (with respect to a particular property). For example, you may have heard that opposite electric charges attract each other and when two particles with equal but opposite charges meet, their total charge becomes zero (and thus no longer has attractive properties). You may have also heard about the acid versus base distinction in chemistry where acids and bases neutralize each other when you mix them (producing water which has no acidic or basic properties).

A particularly nice example to accommodate my “anti-apple” metaphor is the idea of an antiparticle. Every physical particle has an antiparticle version with identical properties but opposite charge. One thing that’s cool (or uncool, depending on your perspective) about them is that when a particle-antiparticle pair meets, they destroy each other!

Take a look at this awesome 3-minute video by minutephysics for a quick introduction to the subject (and a warm-up for today’s main subject):

You can basically think of an antiparticle as the “evil twin” of its particle. Because the two twins are equal in strength (but opposite in intentions), when they meet, their battle leads to their mutual destruction (… and the energy that is released as a result).

Negative numbers as opposites of natural numbers

Let’s go back to the borrowing apples example from earlier. I came up the metaphorical “anti-apple” to represent a debt of one apple. As far as the objective total number of apples you own is concerned, every anti-apple will effectively cancel out an actual apple you get. If you owe 2 apples and someone gives you 4 apples tomorrow, you will eventually have to use 2 of those to cancel your debt. And similarly, if you already have 3 apples and somehow you acquire a debt of 1 apple, you effectively only have 2 apples.

In a way, we can think of natural numbers and their negatives as each other’s antiparticles. When a single apple and a single anti-apple (a debt of 1 apple) meet, they annihilate each other. Well, it turns out this “meeting” process is nothing but the good old addition. Which means the number that represents the result of their addition is the good old zero. If you owe N number of apples and you find N apples somewhere, the effective total number of apples you owe will be zero because each of the N apples will be used to cancel one of the N anti-apples. In the end, you will be left with no apples or anti-apples.

Here’s a short video (the very first video on my new YouTube channel) which visually illustrates this process of canceling out:

Every time you borrow an apple from someone, it’s like they’re separately giving you an apple and an anti-apple. If you eat the apple, you’re left with an anti-apple, which means that one of the next actual apples you get in the future will be annihilated by the anti-apple you have (when you decide to return your debt).

Now imagine that you start out with 3 apples and acquire a new debt of 2 apples. Here, after the 2 anti-apples annihilate 2 of the actual apples, you’re left with a single apple:

On the other hand, if you acquire a debt higher than the number of apples you started with, you’ll be left with only debt:

Finally, if you acquire a debt that is exactly equal in count to what you started with, you’ll simply be left with nothing:

Now let’s take a deeper look at addition and the remaining arithmetic operations with this new kind of number!

Operations with negative numbers

Alright, now that we have a good feeling for what these new numbers represent, let’s see how the familiar operations work with them. The name of the game is “consistency”. We want to make sure that these operations behave the same way even when we extend the set of numbers to include negative numbers. This means that we shouldn’t need to redefine the operations in any way and they should retain all of their old properties.

Before we start exploring binary operations, let me briefly introduce two unary operations that only make sense after we know about negative numbers.

The first is called the absolute value operation (or function). If a is any number, the notation for its absolute value is |a| and it returns the positive version of the number. In other words, the absolute value of a natural number is the number itself and the absolute value of a negative number is its positive version:

$|5| = 5$

$|-5| = 5$

You can think of this operation as returning a number’s distance from zero, without taking into account the direction (left or right).

The second is called the sign operation (function) which has the notation $\textrm{sgn } a$ . It returns 1 for positive numbers, 0 for 0, and -1 for negative numbers. For example:

$\textrm{sgn } 3 = 1$

$\textrm{sgn } -5 = -1$

$\textrm{sgn } 0 = 0$

You can use these two operations to break a number into two components: its sign and its absolute value:

$a = \textrm{sgn } a \cdot |a|$

But we’re getting a little ahead of things…

By the way, for readability purposes in most places below I’m going to write negative numbers enclosed in parentheses:

$(-5) = -5$

Though in practice you’ll frequently see parentheses omitted when there’s no ambiguity (for example, when the first number in the operation is negative).

Addition

Earlier we visualized the operation $a + b$ as starting from a and taking b steps to the right. This is how it worked when a and b were both natural numbers. Now let’s see what happens when a or b (or both) are negative.

First, let’s consider the case where a is negative and b is positive. As you’re about to see, applying the rule of taking steps to the right gives us the “canceling out” result we expect. For example, let’s do the addition $(-3) + 4$ . The rule is telling us to start at -3 and make 4 steps to the right:

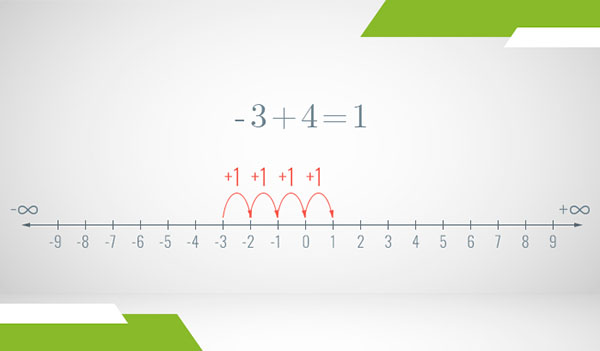
A number line of the integers where addition is illustrated as steps with arrows

So we reached the expected result of $(-3) + 4 = 1$ , This corresponds to, for example, you having 3 “anti-apples” (a debt of 3 apples) and someone gifting you 4 actual apples. The net result is that 3 of the 4 apples cancel out the debt and you’re left with a single apple. Notice that adding a positive number to a negative number is equivalent to subtracting the absolute value of the negative number from the positive number, because:

$4 - |-3| = 4 - 3 = 1$

Therefore, $(-3) + 4 = 4 - |-3|$

and, more generally, if a is negative and b is positive:

$a + b = b - |a|$

Now, following this logic, what should adding a negative number look like? For example, let’s think about the operation $5 + (-2)$

. We know we need to start at the number 5. And, intuitively, we should make two steps, but in which direction? Well, this corresponds to a situation of you having 5 apples and acquiring a debt of 2 apples, right? The net result of adding a negative number is again the same as subtracting its absolute value, so we should be making the steps to the left:

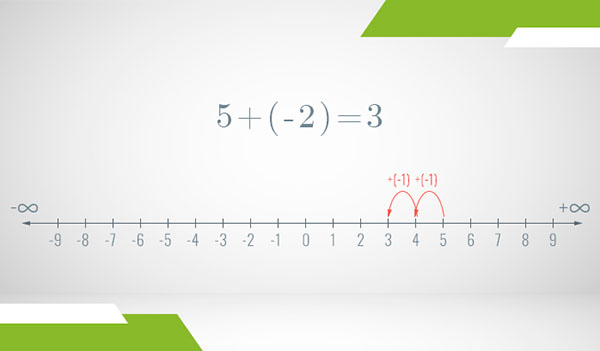
Finally, if we add a negative number to another negative number, the logic is exactly the same. The only difference is that now the starting point is a negative number. For example, if you have a debt of 2 apples and on top of it acquire another debt for 1 apple, you will have a debt of 3 apples:

$$(-2) + (-1) = (-3)$

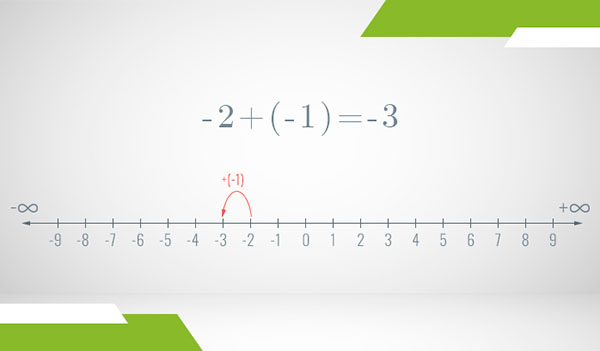
The key intuition is this: adding a negative number is the same as subtracting its positive version (absolute value).

Subtraction

We have defined subtraction as the inverse operation of addition, right? Or, informally, we can think of subtraction as “taking away” stuff. If you have 3 apples and someone takes one of them, you’re left with $3 - 1 = 2$ apples.

Now let’s think about what it means to do subtraction with negative numbers. For example, how can we interpret an expression like:

$(-4) - (-1) = ?$

Well, let’s go back to our apples metaphor. The -4 can represent a state of having 4 anti-apples (a debt of 4 apples). We can then think of subtracting -1 as taking away one of those anti-apples. And you will only be left with 3 anti-apples, right? Then we can say:

$(-4) - (-1) = (-3)$

Notice that the effect of subtracting a negative number is the same as adding its absolute value! That is:

$(-4) - (-1) = (-4) + 1$

And, more generally, for any a and b where b is negative:

$a - b = a + |b|$

So, you see that negative numbers have the property of inverting the operation applied on them. For any pair of numbers a and b, $a + b$

and $a - b$

mean “start at a and make b steps”. Normally, addition and subtraction instruct you to make the steps to the right and to the left, respectively. But if b (the number we’re adding/subtracting) is negative, the direction is inverted. Here’s a summary of all of this:

A table showing the direction to move along the number line when performing addition/subtraction with positive/negative integers — Direction of steps on the number line

Multiplication

If you remember, in the natural numbers post I gave the following intuition about multiplication. For any two numbers a and b, you can think of $a \cdot b$ as adding the number b to 0 a times. For example:

$3 \cdot 2 = 0 + 2 + 2 + 2 = 6$

If we wanted to represent this graphically:

A number line of the integers where multiplication is illustrated as steps with arrows

If the second number is negative instead, it’s pretty straightforward to apply the same rule again. For example:

$3 \cdot (-2) = 0 + (-2) + (-2) + (-2) = 0 - 2 - 2 - 2 = (-6)$

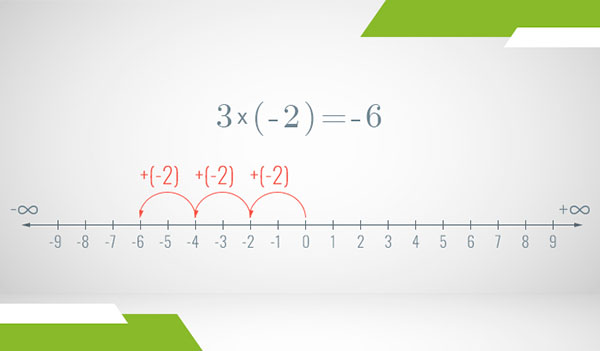
We can again interpret this as something like “debt magnification”. If you already have 2 anti-apples, multiplying them by 3 gets you 6 anti-apples. You have basically tripled your debt.

Now let’s think about what happens if the first number is negative. For example, how can we interpret an expression like:

$(-2) \cdot 3 = ?$

Until now we were interpreting the first number in the operation as a sort of count. It tells us how many times to add the second number to 0. But now suddenly we have a negative count? What does it mean to add a number to zero a “negative number of times”?

By now you must have gotten used to negative numbers’ tendency to invert things. The most straightforward interpretation of multiplying by a negative number is that, instead of adding to zero, we’re going to be subtracting from it. That is:

$(-2) \cdot 3 = 0 - 3 - 3 = (-6)$

That is, we interpret a “negative count” simply as subtraction from zero (instead of addition).

Finally, what happens if both numbers are negative? Well, this case is a combination of the previous two, isn’t it? The second number being negative means that the number we’re adding or subtracting from zero will be negative. And the first number being negative specifies that we need to be subtracting it from zero. For example:

$(-3) \cdot (-2) = 0 - (-2) - (-2) - (-2) = 0 + 2 + 2 + 2 = 6$

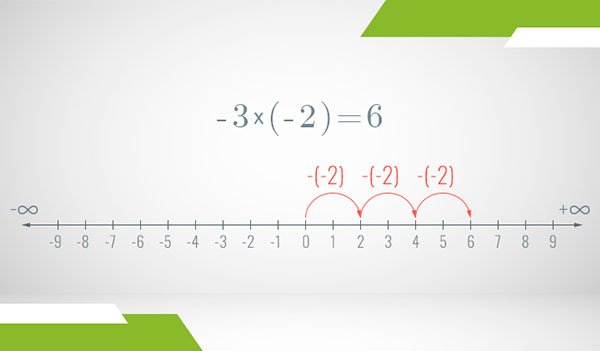
You see that multiplying any two numbers boils down to multiplying their absolute values and maybe changing the sign of the result. If both numbers are positive or both are negative, the product is positive. And if only one of them is negative, the product is negative.

A table showing the the sign of the product when with positive/negative integer multiplier/multiplicand

Compare this table to the table with the rules for adding/subtracting a positive/negative number. Do you see any similarities?

Division

Since multiplication involving negative numbers is identical to natural number multiplication (except for a possible sign change), division is equally straightforward.

Remember, division is the inverse of multiplication and answers the question “What should I multiply the first number by, in order to get the second number?”. For example, $6 \div 3 = 2$ because $2 \cdot 3 = 6$ .

Then, by this logic, it should be easy to convince yourself that:

$(-6) \div 2 = (-3)$

$6 \div (-2) = (-3)$

Because $(-3) \cdot 2 = (-6)$

and $(-3) \cdot (-2) = 6$

, respectively.

Also:

$(-6) \div (-2) = 3$

Because $3 \cdot (-2) = (-6)$

This all shows that division involving negative numbers is also equivalent to division with natural numbers with a possible sign shift. If both the divisor and the dividend are negative, the quotient (result of the division) is positive. And if only one of them is negative, the quotient is also negative.

Division isn’t defined for all pairs of numbers, however. Just like it was with natural numbers, most of the time the dividend won’t divide evenly into the divisor and some part of the dividend will remain undivided. We call that part the remainder. However, this is a somewhat more detailed topic, so I’m going to leave it for a separate post where I introduce the idea of Euclidean division.

Exponentiation, roots, and logarithms

Finally, it’s time to talk about exponentiation and its two inverses. This won’t be a very long discussion because we’ll have to leave the result of these operations undefined for most number pairs. But this is only temporary. It turns out, in order to define those inverses, we need other kinds of numbers, beyond natural numbers and their negative inverses.

What we can define is exponentiation where we’re raising a negative number to a positive power. This works exactly as you’d expect — you simply do repeated multiplication as specified by the exponent. For example:

$(-2)^3 = (-2) \cdot (-2) \cdot (-2) = (-8)$

$(-3)^2 = (-3) \cdot (-3) = 9$

What about negative exponents like:

$(-2)^{(-3)} = ?$

$(3)^{(-2)} = ?$

These will have to remain undefined until the next post from this series because we need new types of numbers to represent their results. That is, the result of raising a number to a negative power is neither a natural number nor any negative whole number.

And the same goes for roots and logarithms involving negative numbers. In the general case, their result will not be within this domain.

The integers

I want to give you the big picture containing both natural numbers and the new number type we discovered today. We used to think that the set of “all numbers” consists of the counting numbers 0, 1, 2, 3, …, all the way to infinity. We called these the natural numbers:

But in our attempts to define the subtraction operation to work for any pair of numbers, we discovered a new type we decided to call negative numbers:

And when we put them together, we obtain the full set of the so-called whole numbers, also known as integers:

Why are they called “whole” numbers? Well, their name only makes sense in the context of the number sets we haven’t talked about yet. And those yet unknown number sets themselves are also named in the context of their supersets. For now, just know that this is the conventional name for the union of the sets of natural and negative numbers. It will all make sense when we reach the end of this series.

Notice that, within the integers, we technically no longer even need the subtraction operation. Why? Because we can represent any subtraction as the addition of the inverse of the number we’re subtracting. For example:

$5 - 3 = 5 + (-3) = 2$

$6 - (-2) = 6 + 2 = 8$

I’m showing you this in order to further draw your attention to the “inversive” properties of negative numbers, as well as to the “inverse” relationship between addition/subtraction and positive/negative numbers.

The typical convention in mathematics is to use the blackboard bold Z to represent the set of all integers and the letter N for the set of all natural numbers:

$\mathbb{N} = \{0, 1, 2, 3, ..., \infty\}$

$\mathbb{Z} = \{-\infty, ..., -3, -2, -1, 0, 1, 2, 3, ..., \infty\}$

Properties of operations with integers

To be sure these new numbers indeed behave like numbers, we need to make sure that all properties of the familiar arithmetic operations still hold when we use them on any pair of integers. That is, extending the set of numbers from naturals to integers shouldn’t make any of the properties change or disappear.

We actually implicitly proved most of the properties I talked about in the previous post. I want to leave it as a small exercise for you to convince yourself that the way we defined addition and multiplication with negative numbers leaves their commutative and associative properties intact. Meaning, for any three integers a, b, and c:

$a + b = b + a$

$a + (b + c) = (a + b) + c$

And:

$a \cdot b = b \cdot a$

$a \cdot (b \cdot c) = (a \cdot b) \cdot c$

It’s also easy to see that the distributive property of multiplication over addition (and subtraction) still holds:

$a \cdot (b \pm c) = (b \pm c) \cdot a = a \cdot b \pm a \cdot c$

Also, when a is a natural number, the right distributive property of exponentiation over multiplication (and division) still holds:

$(b \cdot c)^a = b^a \cdot c^a$

$(b \div c)^a = b^a \div c^a$

And, finally, the additive law of exponents (when b and c are natural numbers):

$a^b \cdot a^c = a^{b + c}$

Coming back to addition and multiplication, it’s also easy to verify that 0 and 1 (respectively) are still the identity elements of these operations. But now, for the first time, we can also talk about the inverse element property of addition. If you remember (from my arithmetic properties post), applying an operation to an element and its inverse element always results in the identity element under that operation. Well, now the “antiparticle” metaphor should make even more sense. Adding any number to its inverse results in 0, which is the identity element under addition:

$5 + (-5) = (-5) + 5 = 0$

And, more generally, for any natural number a:

$a + (-a) = (-a) + a = 0$

You see that 0 is this special number that is neither positive nor negative. Within addition, it has no power to cancel out and it is its own inverse:

$(-0) = 0$

Why do arithmetic properties generalize so easily to negative numbers?

I said I would leave the proofs of the commutative, associative, and distributive properties as an exercise for you. And by that I meant analytic proofs involving arbitrary integers a, b, and c. But let me give you some general intuition for why there’s almost no need for these proofs and how they follow naturally from the already established properties for natural numbers.

The main intuition is that, before we let them annihilate each other, the positive and negative numbers that are being added or multiplied together can be treated merely as “numbers”. The apple/anti-apple metaphor is really useful to illustrate this. To see why, let’s review the intuition I gave for some of these properties in my post on natural numbers.

For example, I gave you the following intuition for the commutative property of addition:

A picture of two red and three green apples (commutative property of addition)

A picture of three green and two red apples (commutative property of addition)

When we’re dealing with real apples, their relative positions to each other don’t affect their final count. So, if we have 2 red and 3 green apples, their total count will be 5 regardless of which group is on the left or on the right.

By identical logic, we also established the associative property of addition:

A picture of 3 green, 2 red, and 2 yellow apples illustrating the associative property of addition

But now imagine that, say, the red apples in these examples are replaced by anti-apples. Before they annihilate each other, we can just treat the mixed group of apples and anti-apples as a group of “objects”. Regardless of the order in which we put them, their total count doesn’t change. And, once we “let” them “destroy” each other, the anti-apples will start knocking out real apples one by one. In the end, you’ll be left with only apples or only anti-apples, depending on which you had more of in the beginning, regardless of their order.

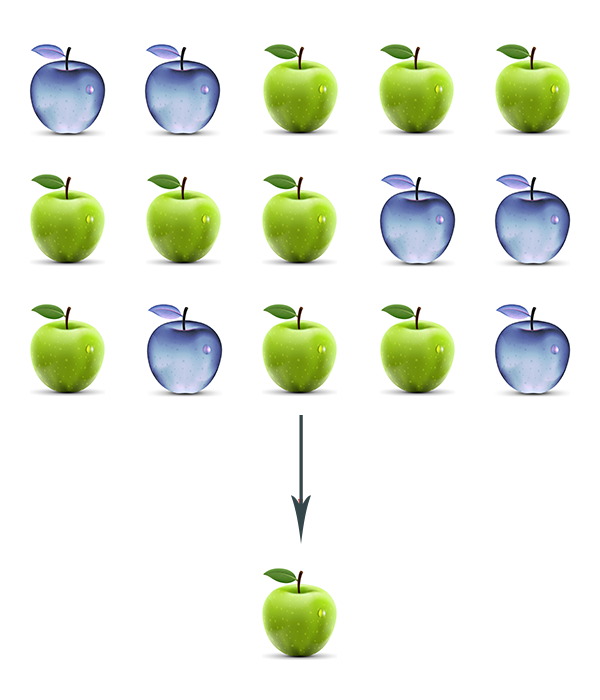
A picture of two purple and three green apples (commutative and associative properties of integer addition)

In this image, we have a total of 5 “objects”, 3 of which are apples and 2 of which are anti-apples, in three different orders. But whatever the order is, two of the apples will be cancelled by the two anti-apples and the net result will always be a single apple.

Summary

Today’s journey was started by the motivation to find meaning for the result of subtracting a natural number from another, smaller, natural number. This led us to the “other side” of the number line which had been dark until now. Which is how we discovered negative numbers.

Once we discovered them, we wanted to:

Find real-world things that they may represent.
Make sure they do behave like numbers when we apply the familiar arithmetic operations on them.

For the first, the most straightforward real-world concept negative numbers stand for is debt. Here we’re really talking about the general concept of debt where a negative number a stands for a debt of |a| (apples, dollars, or whatever you’ve acquired debt for). More generally, you can also intuitively think of negative numbers as “negative counts”. The concept of ‘debt’ isn’t something that physically exists somewhere. In a way, it’s like an agreement between two parties. Therefore, negative numbers describe the state of “having to give something” or “lacking something”. So, you see that, as we enter the world of negative numbers, things are getting a little more abstract (though they are still pretty intuitive and relatable).

Even more generally, we can treat a negative number like a word preceded by “not” in English. For which I gave you the “antiparticle” metaphor from physics. Just like “not” inverts adjectives into their opposites, so does the “minus” sign for numbers — it makes a positive number negative and vice versa:

$-(3) = -3$

$-(-3) = 3$

$\textrm{not Cold} = \textrm{Hot}$

$\textrm{not (not Cold)} = \textrm{not Hot} = \textrm{Cold}$

This interpretation also helps us in getting the intuition for why negative numbers behave just like positives when it comes to arithmetic operations. At least for the four main operations (addition, subtraction, multiplication, and division) we saw that they all work as expected, with the commutative, associative, and distributive properties intact.

However, negative numbers didn’t solve all our problems. We still can’t divide all number pairs and the situation with exponentiation and its inverses (roots and logarithms) is even messier. But, one problem at a time. By the end of this series we’re going to have addressed (almost) all of them.

Anyway, this is it for today. As always, feel free to leave a comment below if you have any questions or feedback!