Combinatorics is a branch of mathematics with applications in fields like physics, economics, computer programming, and many others. In particular, probability theory is one of the fields that makes heavy use of combinatorics in a wide variety of contexts.
For example, when calculating probabilities, you often need to know the number of possible orderings or groupings of events, outcomes of experiments, or generally any kind of objects.
Here’s what I’m talking about.
You can think of probabilities as measures of uncertainty in the occurrence of an event, the truth of a hypothesis, and so on.
These measures are numbers between 0 and 1. Zero means the event is impossible to occur and 1 means the event is certain to occur.
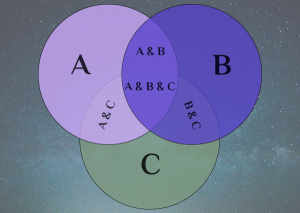
If you have many events of interest, you can measure their probabilities separately, but you can also measure probabilities of different combinations of these events.
Say you’re following the national soccer championships of England, Spain, and Italy. You want to calculate the probabilities of Arsenal, Barcelona, and Juventus becoming national champions next season. These probabilities are:
But what if you want to calculate the probability of both Arsenal and Barcelona becoming champions? Or the probability that at least one of the three teams does?
In this post, I’m going to show how probabilities of such combinations of events are calculated. I’m going to give the general formulas, as well as the intuition behind them. To do that, I’m first going to introduce a few relevant concepts from probability theory.
The concept of a sample space is fundamental to probability theory. It is the set of all possibilities (or possible outcomes) of some uncertain process.
For example, the sample space of the process of flipping a coin is a set with 2 elements. Each represents one of the two possible outcomes: “heads” and “tails”. The sample space of rolling a die is a set with 6 elements and each represents one of the six sides of the die. And so on. Other terms you may come across are event space and possibility space.
Before getting to the details of sample spaces, I first want to properly define the concept of probabilities. [Read more…]