Vigenère and the Age of Polyalphabetic Ciphers

In this week’s post, I’m going to introduce you to the world of polyalphabetic substitution ciphers. And to the most famous cipher from this category: the Vigenère cipher.

This post is part of my series Cryptography: Historical Intro & Combinatoric Analysis.

Where we last left off, I was telling you about cryptography in the ancient world. In the previous post of the series, I showed you two ciphers from the dawn of cryptography: the column cipher and the Caesar cipher.

And today I’m going to talk about how cryptography developed in the following 19 centuries. The focus here is going to be on the birth and evolution of polyalphabetic ciphers. I’m going to show you the Vigenère cipher, which is the most notable example, as well as two related but more advanced ciphers: the autokey cipher and the one-time pad.

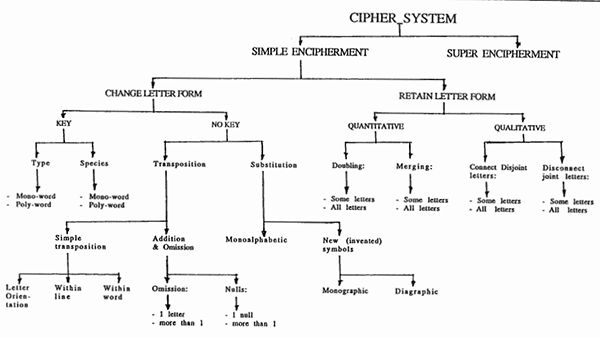
Remember the bigger picture? Cryptographic methods are roughly divided into the categories of codes and ciphers. Ciphers themselves fall under the categories of transposition and substitution ciphers (I showed you an example of each in the previous post). Finally, substitution ciphers are of two general types: monoalphabetic and polyalphabetic.

Monoalphabetic ciphers substitute each plaintext letter with the same ciphertext letter. On the other hand, in polyalphabetic ciphers the same plaintext letter can translate to different ciphertext letters in different positions of the text. In the sections below. I’m going to explain how the 3 ciphers above work and give you interesting historical context around their invention and usage.

Of course, like in all posts of the series, using a combinatoric analysis, I’m going to show you how to calculate the total number of possible keys of each cipher. The purpose is to evaluate the brute-force security score of the ciphers (from 1 to 10).

Overview of cryptography in the Common Era

In the last post, I tried to give you a sense of what cryptography was like before the Common Era. Apart from a few tentative attempts, it wasn’t really developing yet. One of the main reasons was the very low rates of literacy across the world at the time.

Well, in the first 15 centuries of the Common Era, partly due to the rise in literacy, the interest in cryptography started increasing. But things were still chaotic. Cryptography was developing independently in different parts of the world and new methods were hardly building on top of previous ones. In terms of lasting knowledge, more was lost than retained.

Cryptography in the East

There is some historical evidence that Persians started using cryptography in the first few centuries for political purposes. The 10th century Arab chronicler Ibn al-Nadim mentions a script called shāh-dabīrīya which Persian royalty used between the 3rd and 7th centuries for communicating between each other secretly from regular people. He also mentions another script called rāz-sahrīya that Persians used for secret communication with foreign nations.

The 11th century Chinese military collection Wujing Zongyao recommended a small code for military communication that is very similar to the color code example I gave you in the introductory post (“red” = “we are surrounded”, “green” = “attack at dawn”, etc.). Instead of colors, the Chinese system used the first 40 ideograms of a poem as the code symbols to represent messages like “I need more bows and arrows”, “we were victorious”, and so on. Other than that, surprisingly enough, cryptography wasn’t really used in China in this period.

In the 9th century, the Arabic scientist Al-Kindi wrote a book called “Risalah fi Istikhraj al-Mu’amma” (A Manuscript on Deciphering Cryptographic Messages). This was an extremely valuable resource on cryptography and is probably the oldest systematic book in the field. In the book, Al-Kindi classified cryptographic methods in a way that is remarkably similar to today’s classification.

Al-Kindi was by no means the only Arabic contributor to the field. Cryptography was flourishing in the Arab world during the Islamic Golden Age and many other authors like Al-Khalil, Ibn ‘Adlan, and Al-Qalqashandi also had important contributions.

Cryptography in the West

During the same period, Europe was lagging behind its eastern neighbors in many areas, including cryptography. In the first few centuries, some rudimentary cryptographic methods were used in the Roman Empire that were similar or modified versions of older ciphers from the Caesar period.

Before the adoption of the Latin alphabet, some European regions had the so-called runic alphabets. The letters in these alphabets were divided into 3 groups and each letter had a specific order in its group. In Scandinavia, starting around the 8th century, there were different substitution ciphers for encrypting texts written in runic alphabets. These ciphers revolved around replacing letters with 2 numbers: one indicating their group and one indicating the letter number in the group (for example, by a corresponding number of short/long vertical marks). A famous example of a runic cipher was found on the 9th century Rök runestone in Sweden:

Unfortunately, around that time Europe had started slipping into the (“Dark”) Middle Ages. After the collapse of the Roman Empire in the end of the 5th century, literacy levels started dropping and interest in subjects like arts and sciences was very little. Until around the 14th century, there was hardly any cryptography in Europe. In the Middle Ages, things like codes and ciphers were associated with dark magic and other esoteric practices. So, not only was there low interest, but people generally didn’t look kindly on cryptography.

By the late Middle Ages and the beginning of the Renaissance period, this started to change. Starting from the 14th century, there was a sharp rise in cryptography’s development in countries like Italy, Germany (then known as the Holy Roman Empire), Spain, England, and France. Five-ten centuries after the Arabs, Europe was finally taking cryptography seriously!

And cryptography’s development never stopped ever since.

The birth of polyalphabetic ciphers

Polyalphabetic substitution ciphers were first discussed by Arabs. For example, Al-Kindi talked about them in the 9th century in his book “Risalah fi Istikhraj al-Mu’amma” I mentioned earlier. Although other Arab authors also talked about polyalphabetic ciphers in the next few centuries, this knowledge failed to spread over the world.

Polyalphabetic ciphers were independently discovered in Europe in the 15th and 16th centuries. The first polyalphabetic cipher was invented by the Italian author Leon Battista Alberti in the 15th century. His overall work in cryptography was so important that he earned the title “Father of Western Cryptography”.

In the 16th century, the German author Johannes Trithemius and the Italian author Giovan Battista Bellaso invented two other methods for polyalphabetic substitution which, together with Alberti’s method, became the basis of the Vigenère cipher and the other two related ciphers I’m going to show you in a bit.

Let me first show you these earlier ciphers.

Alberti’s cipher

One of Alberti’s inventions was a cipher disk that consisted of two circles made of copper plates. The smaller circle was inside the larger one and it could be rotated relative to it.

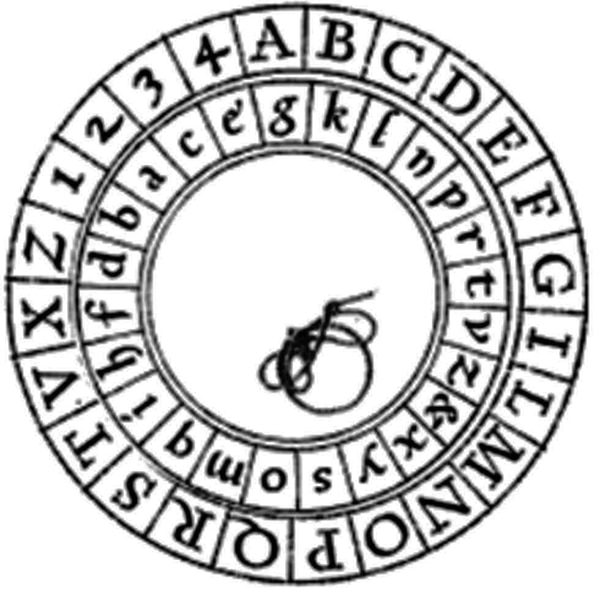
The two circles were both divided into 24 equal parts, each part containing a symbol. The large circle had all uppercase letters in the Latin alphabet (except H, J, K, U, W, and Y) in their proper order, as well as the numbers 1 through 4. The smaller circle had all lowercase letters (except j, u, and w) in a random order, as well as the ‘&’ symbol. Some of the missing letters aren’t part of the Italian alphabet and others Alberti considered “not necessary”.

One of the letters in the small circle (let’s say ‘a’) was used as an index letter. The position of the small circle is then indicated by the symbol on the large circle above the index letter (in the above image, it’s at 2).

The letters on the large circle represent plaintext letters and those on the small circle represent their corresponding ciphertext substitutes. Therefore, each of the 24 possible positions of the small circle specifies a different substitution rule with which words should be enciphered.

But here’s the trick! With every few words, the position of the index letter was changed and the next few words were enciphered with a different substitution rule. This means that the same plaintext letter now turns to different ciphertext letters in different positions (words) of the message. Thus, polyalphabetic substitution ciphers were born in Europe!

The key in Alberti’s cipher

In modern terms, the key of this cipher consists of a sequence of letters indicating the position of the small circle (its index letter), as well as the words at which to switch the position. However, that’s not how Alberti used it.

Alberti suggested the final message should be a mixture of lowercase ciphertext letters and uppercase plaintext letters inserted at the right positions. These uppercase letters indicated the new position of the small circle for the next few words. In other words, the secrecy of this cipher depended on the secrecy of the procedure itself. Alberti’s cipher doesn’t have a key and hence doesn’t conform to Shannon’s Maxim I told you about in the introductory post.

Trithemius’ cipher

Do you remember the tabula recta I showed you in the Caesar cipher section of my last post? Well, it was actually invented by Johannes Trithemius in the beginning of the 16th century.

Let me explain it with an analogy to Alberti’s cipher disk.

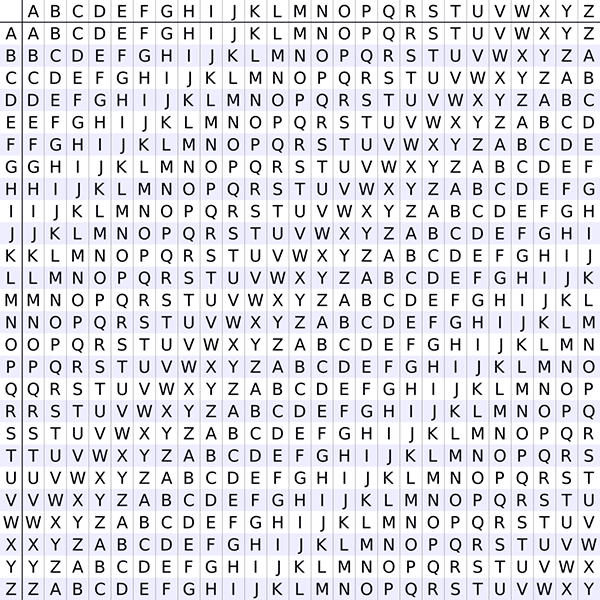
The letters of the leftmost column are the labels of the 26 rows in the table. Each row is the Latin alphabet shifted by 0 to 25 steps and serves the role of the small circle in Alberti’s disk. The topmost row is like the large circle and serves as a reference for the plaintext letters. In other words, each row specifies a different substitution rule. For example, row B’s rule is:

A->B, B->C, C->D, …, Z->A

Trithemius’ cipher was very simple. He enciphered each letter in the plaintext with the next row of the tabula recta, starting from the first and going in order. For example, if he wanted to encipher “hello”, he would apply the substitution rules of rows A, B, C, D, and E on the letters ‘h’, ‘e’, ‘l’, ‘l’, and ‘o’, respectively. The final ciphertext becomes “hfnos”.

A glaring weakness of this cipher is that it also lacks a key! So, anybody aware it’s being used is in the same position to decipher messages as are intended recipients of those messages. And, like Alberti’s cipher, this is another direct violation of Shannon’s Maxim.

In a more “advanced” version of this cipher, you also specify the initial row (instead of starting from the A row by default). But that just makes the cipher as secure as the Caesar cipher, which also has only 26 possible keys.

Still, Trithemius’ cipher and the tabula recta were important steps in the development of polyalphabetic ciphers.

Bellaso’s cipher

Giovan Bellaso built a cipher combining the ideas of Alberti and Trithemius. He invented an alternative to the tabula recta which he called a reciprocal table. He split the 22-letter Italian alphabet (ABCDEFGHILMNOPQRSTVXYZ) in half and put the two halves into 2 rows. Then he listed 11 different shifts of the bottom row relative to the top row which created 11 different row pairs. Bellaso labeled each pair with a pair of consecutive letters from the alphabet.

Notice, the shifts in the bottom rows are made the same way as the shifts in the tabula recta (the alphabetic order is preserved) but the row pairs themselves are ordered randomly. Each row pair specifies a reciprocal substitution rule. For example, the ST rows specify the substitution rule:

a<->p, b<->q, c<->r, d<->s, e<->t, f<->v, g<->x, h<->y, i<->z, l<->n, m<->o

So, how did Bellaso use this table to encipher messages?

Before you begin enciphering a message, you first need to choose a keyword (the cipher key). This can be any word. Then, you write the keyword on top of a message by repeating it throughout its length. For example, if your keyword is “axe” and the plaintext is “hello”, you do:

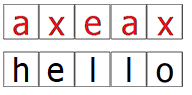
Then, you substitute each plaintext letter by the rule specified by the keyword letter above it. If the letter is ‘a’ or ‘b’, you use the AB rule, for ‘c’/’d’, you use the CD rule, etc.

In this example, the first letter ‘h’ should be substituted with the AB rule and it becomes ‘v’. The second letter ‘e’ is substituted with the VX rule, so it becomes ‘n’. The full ciphertext is “vnxyf”.

Now this is a polyalphabetic cipher with a properly variable key!

The Vigenère cipher

The Vigenère cipher is arguably the most famous polyalphabetic cipher. Its invention is also in the 16th century and until the middle of the 19th century most people considered it unbreakable.

The name of the cipher comes from the 16th century French cryptographer Blaise de Vigenère. But not because he was the one who invented it. Actually, the whole story of this cipher’s name is rather strange. And it’s not exactly known who really invented it.

People commonly say that the Vigenère cipher is wrongly attributed to Blaise de Vigenère and its real inventor was Giovan Bellaso. But as you’ll see below, the Vigenère cipher isn’t exactly identical to Bellaso’s cipher. In fact, the Vigenère cipher is a hybrid between Bellaso’s cipher, Trithemius’ cipher, and the autokey cipher I’m going to show you later.

The strangeness doesn’t end here. The autokey cipher itself was invented by… Blaise de Vigenère. Yes, I know it’s a bit confusing, but at this point the terminology is what it is. This confusion was most likely created because there was a 2-3 century gap between the invention of the Bellaso and autokey ciphers and the widespread use of what people now call the Vigenère cipher.

Anyway, let’s see how the Vigenère cipher works.

Details of the Vigenère cipher

If you already understand Caesar’s, Trithemius’, and Bellaso’s ciphers, you will have no difficulty understanding the Vigenère cipher as well. On the one hand, it’s simply an advanced version of the Caesar cipher. Or, another way to put it, the Caesar cipher is a special case of the Vigenère cipher. On the other hand, it’s almost identical to Bellaso’s cipher but it’s based on Trithemius’ tabula recta, instead of Bellaso’s reciprocal table. Here’s how it works.

Like Bellaso’s cipher, you choose a keyword that you repeatedly write over the plaintext. For example, if the keyword is “axe” and the plaintext is “we are surrounded”, you do:

Then, based on the tabula recta, you shift each letter in the plaintext by a number specified by the key letter above it. Meaning, you apply a Caesar cipher locally for each letter.

For example, the first letter ‘w’ should be enciphered with the key A, which is simply a shift of 0, so it remains ‘w’. The next letter ‘e’ should be enciphered with the key X, so it becomes ‘b’. The final ciphertext becomes “wb erb wuovorrdbh”.

Decryption works in the opposite direction. You repeatedly write the keyword on top of the ciphertext and perform a negative shift for each letter.

You also see why the Caesar cipher is a special case of the Vigenère cipher, right? If not, just look at what happens when you use it with a keyword that is only one letter long.

The Vigenère cipher during the American Civil War

Now let’s jump across the Atlantic Ocean to the continent of North America.

While polyalphabetic ciphers were busy being discovered in the 15^th and 16th centuries in Europe, other Europeans were making the first steps in colonizing the “New World”. The first colonies in North America started appearing in the beginning of the 17th century and, by the middle of the 18th century, their number was 13.

These colonies were under British rule and locals didn’t like that very much. This lead to the (successful) War of Independence (1775–1783) after which the 13 colonies became the 13 states. Which gave birth to a new country on the world map: the United States of America! The officially celebrated date is the 4th of July related to the Declaration of Independence from 1776.

One of the most important events in this new country’s history took place less than a century later. Namely, the American Civil War between 1861 and 1865.

Before this war, the United States was informally divided between the North and the South. They were divided politically, socially, and economically. At the time, the North was seeing a rapid industrialization, whereas the South relied on more traditional agriculture to sustain and grow their economy.

A central cause for the war was the issue of slavery. In the previous few decades, northern states had already abolished it and they were also known as free states. On the other hand, southern states’ agricultural economy was dependent on slavery and they were known as slave states.

Overview of the conflict

For a period, there was an equal number of free and slave states. But, as new states joined the union, the free states grew in number and southern states were worried about losing political influence. One of their fears was that the North was eventually going to ban slavery across the country.

All this tension culminated after the 1860 presidential elections. Then, Abraham Lincoln, the leader of the newly formed Republican Party, won a convincing victory. Lincoln was very outspoken against slavery. And, despite reassurances that he had no intention to intervene in the southern states’ internal affairs regarding slavery, the southern states didn’t trust him. So, they decided to secede and form their own country.

The seceding states would later become the Confederate States of America and would be opposed to the northern United States of America.

Long story short, war broke out in April 1861 when South Carolina (one of the slave states) militias attacked and took over Fort Sumter, a federal military fort. Shortly after, the Confederate Army was formed and would be in a 4-year-long war against the Union Army. At the end of it, Union forces were victorious. Confederate states were taken back and slavery was officially abolished once and for all.

To this day, the Civil War is the largest military conflict in US history. In some ways, it was foreshadowing some of the features of World War I half a century later (which is the topic of one of the next posts in this series). These similarities include:

• Elements of total war
• Trench warfare
• Naval blockades
• Large-scale secret communication

Interesting as they are, the details of the war are beyond the scope of this post. So, let me focus on the last of these points.

Military communication during the Civil War

During the war, there were two main types of military communication. The first was short-distance communication between different military units and their commanders. This type was concerned with military tactics. The second type was long-distance communication and was more about communicating military strategy.

You need to remember that, at the time, communication technologies themselves were very different and much less developed. So how did they do it?

Well, for long-range communication, they still relied on traditional letters. But since about 25 years before the war, the electric telegraph had also been making its way as a method of communication. Some time after the outbreak of the war, the military on both sides adopted it.

The usage of the electric telegraph during the US Civil War is an important point in the history of cryptography. With it, fast and secret military communication became possible for the first time in organized warfare.

Another method that was also widely used for short-range military communication (particularly by Union forces) was visual signaling, also known as “aerial telegraphy” or “wig-wag signaling“.

This involved sending visual signals with flags during the day and torches during the night. Different types of motions with the flags (left, right, up, down, etc.) indicated different symbols. And combinations of symbols stood for things like letters from the alphabet and the numbers 0 through 9. If you’re curious, you can read more about this communication system here.

At first, both sides sent all their messages in plaintext form. But soon they learned that the messages were being intercepted and had to do something to protect their secrecy (both for tactical and strategic communication).

Cryptography and the Vigenère cipher during the Civil War

The Union Army was using a type of transposition cipher they called a route cipher, which I’ll explain in the next post of the series.

On the other hand, the Confederate Army was using a cipher called the “Court cipher“. Well, without even knowing, they were actually using the Vigenère cipher, but under a different name. According to the US cryptographer William Friedman, this term came from to the fact that, at the time, the Vigenère cipher was commonly used in diplomatic or “court” communication. It could also have something to do with the fact that Vigenère presented his autokey cipher to the French king Henry III in his royal court.

As you can see, even then there was significant confusion about the terminology. But still, now we know that it was definitely the Vigenère cipher that Confederates were using.

They used a special cipher disk to help them encipher and decipher messages. The inner disk was rotatable and could be turned to different positions for a particular alphabetic shift (it was basically simulating a tabula recta). As you can see, this is pretty similar to Alberti’s cipher disk!

By the way, you see the CSA abbreviated in the middle? It stands for (you guessed it) the Confederate States of America.

In some sense, Confederates were a bit lazy in its usage. To our knowledge, they used a very limited number of keys to encipher messages. In fact, let me give you the 4 most commonly used keys:

• Complete Victory
• In God We Trust
• Come Retribution
• Manchester Bluff

And now let me show you some examples of its usage during the war. Particularly, with the last of these keys.

“Manchester Bluff”: secret messages during the Siege of Vicksburg

From the start of the war, one of the major strategies of the Union was to blockade the Confederates. This strategy’s name was the Anaconda Plan.

This basically involved:

1. Cutting Confederate access to ports
2. Taking control over the Mississippi River

Given the geography of the Mississippi River, the second part of this plan would split the South in two. That would divide their forces and they wouldn’t be able to help each other by sending troops or supplies.

In 1863, two years into the war, the city of Vicksburg, Mississippi, was the last major Confederate stronghold on the river. If it fell into Union hands, the Anaconda Plan concerning the river was going to be complete.

And Union forces, led by Gen. Ulysses S. Grant, did manage to capture the city from Confederate Gen. John C. Pemberton. Many historians consider this one of the major turning points of the Civil War.

Grant managed to capture the city after an almost 50 day siege (between the 18th of May and the 4th of July, 1863). Gen. Pemberton’s army was twice as small as Gen. Grant’s, so Pemberton decided to retreat into a defensive position inside the city (which had strong fortifications). At first, Grant’s forces tried to attack, but after a week of unsuccessful attempts and heavy casualties, he decided on a siege. The plan was to starve Pemberton’s forces into submission.

On the 4th of July 1863, Pemberton surrendered to Grant. The date is rather unfortunate, isn’t it? In fact, it’s said that citizens of Vicksburg didn’t celebrate the 4th of July for about 50 years after the war.

Well, with this background information, let’s finally look at two secret messages related to this event.

Gen. Jonston’s letter to Gen. Pemberton, 25th of May 1863

During the siege, Grant’s scouts had captured several cipher-dispatches from Gen. Joseph E. Johnston, addressed to Pemberton. Johnston was another Confederate general who, at the time, was trying to join forces with Pemberton to help him defend Vicksburg.

This is one of those dispatches, captured on the 25^th of May 1863:

I took this from the 1907 book Lincoln in the Telegraph Office whose author David Homer Bates was one of the original four operators of the U.S. Military Telegraph Corps.

The message was enclosed in a letter from Grant to Col. John C. Kelton in Washington, D.C. saying:

So, Gen. Grant wasn’t able to understand what the secret message said. But can you?

If you like, before I show you the full plaintext, try to break it yourself as an exercise. Here’s a few small clues:

• The message is enciphered with the Vigenère cipher and the key is “Manchester Bluff”.
• It’s enciphered only partially. The full message is a mix of plaintext and ciphertext.
• Treat the ciphertext parts of the message independently of the plaintext. Meaning, ignore the existence of any plaintext.
• While deciphering, ignore spaces between words (both in the message and in the key).

To make it easier for you, here’s the message in a more readable form:

My XAFV USLX was VVUFLSJP by the BRCYIJ. 200 000 VEGT SUAJ NERP ZIFM. It will be GFOECSZQD as they NTYMNX. Bragg MJ TPHINZG a QKCMKBSE. When it DZGJX I will YOIG AS QHY. NITWM do you YTIAM the IIKM VFVEY. How and where is the JSQML GUGSFTVE. HBFY is your ROEEL.

Alright, if you tried and managed to solve it, congratulations! And if you had difficulties, don’t worry about it. This is how learning works!

Anyway, here’s the solution.

The solution

First, let’s isolate the enciphered parts of the message:

XAFV USLX VVUFLSJP BRCYIJ VEGT SUAJ NERP ZIFM GFOECSZQD NTYMNX MJ TPHINZG QKCMKBSE DZGJX YOIG AS QHY NITWM YTIAM IIKM VFVEY JSQML GUGSFTVE HBFY ROEEL

Now, we need to decipher this with the key “Manchester Bluff”. Like I said, we ignore spaces and simply write “MANCHESTERBLUFF” repeatedly to match the length of the ciphertext.

MANC HEST ERBLUFFM ANCHES TERB LUFF MANC HEST ERBLUFFMA NCHEST ER BLUFFMA NCHESTER BLUFF MANC HE STE RBLUF FMANC HEST ERBLU FFMAN CHESTERB LUFF MANCH

And now we’re ready to break the cipher. Let’s start with the first word. We need to apply the following negative shifts to the letters X, A, F, and V:

• M (-12)
• A (0)
• N (-13)
• C (-2)

X shifted by -12 is L. A shifted by 0 is A. F shifted by -13 is S. V shifted by -2 is T. So, the XAFV ciphertext block corresponds to the plaintext LAST.

When we repeat this procedure for the whole ciphertext, it turns into the following plaintext:

LAST NOTE RETURNED BEARER CAPS HAVE BEEN SENT CONTINUED ARRIVE IS SENDING DIVISION COMES MOVE TO YOU WHICH THINK BEST ROUTE ENEMY ENCAMPED WHAT FORCE

And, finally, we put back the deciphered blocks in their original place in the message:

My LAST NOTE was RETURNED by the BEARER. 200 000 CAPS HAVE BEEN SENT. It will be CONTINUED as they ARRIVE. Bragg IS SENDING a DIVISION. When it COMES I will MOVE TO YOU. WHICH do you THINK the BEST ROUTE. How and where is the ENEMY ENCAMPED. WHAT is your FORCE.

Easy, isn’t it?

Gen. Walker’s letter to Gen. Pemberton, 4th of July 1863

On the 4th of July, the day of Pemberton’s surrender, Gen. John G. Walker (another Confederate general) tried to send him a message. Given the date of the message, we can guess that Walker most likely didn’t know about the hopeless situation in Vicksburg.

He sent the message through one of his loyal captains, Capt. William A. Smith. The letter with the message was put in a tiny bottle along with a .38-caliber bullet. The bullet was most likely there to make the bottle sink to the bottom of the river in case it needed to be tossed (if in danger of being captured by enemy forces).

But the message obviously never made it to its destination. After learning of Pemberton’s surrender, Capt. Smith kept the bottle as a souvenir for himself and in 1896 donated it to the Museum of the Confederacy (now part of the American Civil War Museum).

It wasn’t until 2010 that the bottle was actually opened by a curious collections manager of the museum and deciphered by a retired CIA code breaker.

Actually, deciphering this message was harder than usual because of a few errors in the ciphertext. The errors are small, but due to the nature of the Vigenère cipher, even a single extra or missing letter in the ciphertext can ruin deciphering. So, let me give you the ciphertext in a cleaned up form:

sean wieuiiuzh dtg cnp lbhxgk oz bjqb feqt xzbw jjoy tk fhr tpzwk pvu rysq voupzxgg oeph ck uasfkipw plvo jiz hmn nvaeud xyf durj bovpa sf mlv fyyrde lvpl mfysin xy fqeo npk m obpc fyxjfhoht as etov b ocajdsvqu m ztzv tphy dau fqti uttj j dogoaia flwhtxti qltr sea lvlflxfo

Want to try to decipher it yourself?

The solution

Notice that this time the entire message is in ciphertext. This makes deciphering it more straightforward, but also it takes a bit longer.

Again, all we need to do is repeatedly write “manchesterbluff” to match the length of the message and apply the proper negative shifts to each ciphertext letter. Here’s the result:

genl pemberton you can expect no help from this side of the river let genl johnston know if possible when you can attack the same point on the enemys line inform me also and i will endeavour to make a diversion i have sent you some caps i subjoin despatch from gen johnston

Well, the letter never made it to its destination. But even if it had, judging by its contents, you see that it wasn’t going to be of much help to Pemberton.

Combinatoric analysis of the Vigenère cipher

After all this historical background, let’s finally evaluate the security of the Vigenère cipher.

Let’s establish a few terminological conventions:

• A – the number of letters in the alphabet
• N – the number of letters in the ciphertext
• k – the number of letters in the keyword

Let’s consider the case where we know the length of the keyword. And let’s say it’s only 3 letters long. Also, let’s assume that we’re still dealing with the Latin alphabet of 26 letters. How many possible keywords of length 3 are there?

We basically have 3 slots for letters. And each slot can be occupied by 26 possible letters. Therefore, 26 letters from the first position can be combined with 26 letters from the second position. And each so-formed pair can be combined with 26 letters in the third position. Hence, here we also have a straightforward application of the rule of product:

   

Or more generally, for any keyword length k and any alphabet length A:

   

The general case

If the keyword length isn’t known (as is the case most of the time), then we need to do the above calculation for every possible keyword length and sum the results. And there are N possible keyword lengths: anything from 1 to N (the length of the ciphertext). Therefore, the general formula for the total number of possible keys here is:

   

If you’re not familiar with the above notation (the sum operator), please take a look at my post dedicated to this notation and its properties.

Those of you familiar with geometric series will recognize that the above sum is exactly that. The closed-form solution on the right-hand side of the equation comes from a geometric series formula (which I’m not going to prove here). I’ll introduce geometric and other types of series in future posts. If you’re not familiar with them, don’t worry about it for now.

If the length of the alphabet is 26 and the length of the ciphertext is, say, 15, the number of possible keys would be:

   

Well, this is a huge number which will get uncontrollably larger for even slightly longer messages. So, it’s only practically possible to break the key with a brute-force attack if the message is very short.

The brute-force security score here approaches the levels of security of the double transposition cipher I showed you in the previous post. Therefore, I’m going to give the Vigenère cipher the same security score of 9.

Brute-force security score: 9

Security of earlier polyalphabetic ciphers

Before moving on, let me say a few words about the cryptographic security of the three ciphers I showed you earlier.

Let’s start with Alberti’s cipher. In his original formulation, the cipher didn’t have a key which makes combinatoric analysis irrelevant.

Brute-force security score: 1

The Trithemius cipher also doesn’t have a key in its original formulation. In the more advanced version (with random starting position of the initial shift), it has the same brute-force security as the Caesar cipher. That is, the number of possible keys is equal to the number of letters in the alphabet.

Brute-force security score: 1

Finally, there’s the Bellaso cipher, which is almost identical to the Vigenère cipher. The main difference is that the number of possible shifts is half of the length of the alphabet. This changes the formula for calculating the number of keys to:

   

Again, A is the number of letters in the alphabet and N is the ciphertext’s length. Even though the number of keys will be growing a little slower as N grows, this doesn’t significantly change the overall complexity of the cipher. But just because some shorter messages are easier to break, I’m going to give it a score of 8.

Brute-force security score: 8

Polyalphabetic ciphers related to the Vigenère cipher

In the final section of this post, I want to show you two ciphers that are natural extensions of the Vigenère cipher. One of these ciphers (the autokey cipher) relies on a technique for adding an element of randomness to the key, whereas the other (the one-time pad) takes the idea of a “long key” to its limit.

Let’s take a look at these ciphers.

The autokey cipher

The autokey cipher is very similar to the Vigenère cipher. You still have a keyword that you write on top of the plaintext. However, instead of repeating the keyword for the whole plaintext, here you write it only once and complete the remaining empty spaces with the plaintext itself!

For example, to encipher “we are surrounded” with the keyword “axe”, you do:

Then you encipher the plaintext exactly as you would with the Vigenère cipher, by shifting each plaintext letter by an amount specified by the letter above it. Yes, it’s that simple! The ciphertext we get here is “wb eni slvjileryq”.

How does deciphering work? Well, first you write the keyword on top of the first letters of the ciphertext:

In this case, these are the first 3 letters which can be deciphered in the regular way, by applying negative shifts based on the keyword letters. We get “we a…”. Well, now we can use these 3 letters to fill the next 3 empty spaces. This allows us to decipher the next 3 letters of the ciphertext (…ni s…) and we get “…re s…”. So, now the deciphered plaintext is “we are s…”.

Now we can fill 3 more empty spaces. Continuing like this, we reconstruct the full plaintext.

As you can see, this is like a Vigenère cipher but the key for each message is unique to the message. That’s a pretty clever idea for adding natural randomness to the key, which makes this cipher much harder to break with methods other than brute-force.

History of the autokey cipher

Earlier I told you that the autokey cipher was invented by Blaise de Vigenère, right? Well, in his version of the cipher, he used a single letter to “prime” the key and filled the remaining empty spaces above the plaintext with the plaintext itself. In other words, the actual key (shared between correspondents) was a single letter. I’m not sure why Vigenère limited his cipher in this way, given that it made it extremely insecure. Still, people associate the general version of the cipher I showed you with him.

Vigenère himself was familiar with the works of Alberti, Trithemius, and Bellaso. So, the link between the autokey cipher and the earlier ciphers I showed you is clear. Another cipher that contributed to Vigenère’s idea was by another Italian author, Gerolamo Cardano.

Cardano invented the same cipher, except he didn’t use any keyword but just wrote the plaintext on top of itself and enciphered it with itself. As you can guess, since his cipher lacks a key, it’s extremely insecure. Vigenère “improved” it by adding a single priming letter at the beginning, which wasn’t really much of an improvement. But at least it was a special case of a more general idea that created a powerful cipher.

Actually, Bellaso himself had invented a different type of “autokey” cipher a little earlier, which probably also influenced Vigenère.

Bellaso’s autokey cipher

Bellaso was using a variant of his original cipher where the row pairs and the bottom pair in each pair of his reciprocal table were shuffled according to a keyword. The method involved enciphering each plaintext letter with the rules specified by the row pairs in their original order. That is, the first plaintext letter is enciphered with the first row pair, the second letter with the second row pair, and so on. When you’ve used the 11^th row pair, you simply loop back to the first.

In addition, at the first letter of every word, you skip the regular order and jump to the the row pair containing the first letter of the previous word. For example, if the first letter of the first word is B, at the first letter of the second word you move to the row pair AB (or whichever row pair has B in it) and continue enciphering from there.

Frankly, Bellaso’s autokey cipher was much more secure than Vigenère’s. So, why don’t we attribute its invention to him? Well, we probably should, but I’m not sure if this is so important.

For what it’s worth, the earliest mention of the term “autokey cipher” I could find was in the 1949 paper Communication Theory of Secrecy Systems by the legendary cryptographer Claude Shannon (remember Shannon’s Maxim?). There, he describes the procedure I showed you above (Vigenère’s version of the autokey but with a priming word, instead of a single letter). So, the real inventor of what we call “the autokey cipher” today could be Shannon himself. And since Shannon also introduces the Vigenère cipher in the same paper, most likely he is the one who coined that term as well.

Combinatoric analysis

The combinatoric analysis of the autokey cipher is identical to that of the Vigenère cipher, since the keyword can be as long as the plaintext and each letter can be any of the 26 possibilities.

But keep in mind that this is true only in the context of brute-force attacks. In general, using other methods for breaking polyalphabetic substitution ciphers, the autokey cipher is much more secure. But that’s a topic for another conversation (another post).

Brute-force security score: 9

The one-time pad

The last innovation in cryptography related to the Vigenère cipher I want to talk about is the one-time pad.

We already know that the Caesar cipher is a (much less secure) special case of the Vigenère cipher, right? The reason for its lack of security is the fact that the number of possible keys for any message is too small. Like I showed you in the combinatoric analysis section for the Vigenère cipher, the number of possible keys for any given key length (k) is equal to (A = length of alphabet). Given this relationship, the longer the key is, the more difficult it is to break it.

As a method, the one-time pad came from taking this idea to the extreme.

What if every message is enciphered with a keyword as long as the message itself? Not only that, but what if the keyword isn’t an actual word or phrase but a completely random sequence of letters? And what if this keyword is unique to every message and the same keyword is never intentionally used more than once?

Any cryptographic method following these three criteria falls under the definition of a one-time pad. And any method that doesn’t follow even one of them is not a one-time pad.

For example, let’s encipher “we are surrounded” in the style of Vigenère but the keyword being a randomly generated sequence of letters as long as the message:

The ciphertext here becomes “mi mtd hnthbaxmzv“.

Using the one-time pad

In a typical implementation of this cipher, you generate a very long random sequence of letters and share it in advance with another person. The idea is to use different pieces of this sequence as keywords for different messages. And you indicate this by writing your starting position in the sequence at the beginning of each message.

For example Alice and Bob generate a sequence of 10 000 random letters and each save a copy before splitting. Then, let’s say Alice wants to write Bob a message that’s 100 letters long. She enciphers the message with the first 100 letters of the sequence and sends the ciphertext along with the phrase “position 1”. Then Bob replies with a 60 letter long message which he enciphers with the letters 101-160 and sends the ciphertext along with “position 101”.

Sharing this position in clear isn’t a problem because it won’t be of any help to potential eavesdroppers if they don’t have access to the actual letter sequence. And sharing it is important, in order to avoid potential errors, especially if more than 2 parties are using the same letter sequence to generate keys for their messages.

History of the one-time pad

A cryptographic system conforming to the definition of a one-time pad was first described at the end of the 19th century by a US Civil War veteran. His name was Frank Miller but not much is known about his work.

But we know that in 1882 he created a codebook in which he described a method of encipherment involving shifting letters using modular arithmetic. He emphasized that the shifts must be random and never reused, which are the requirements of the one-time pad.

But at the time Frank Miller’s work didn’t receive any attention and it was rediscovered quite recently. That’s why most people associate the invention of the one-time pad with another American engineer and cryptographer, Gilbert Vernam. Although there’s some possibility that Vernam was indirectly inspired by Miller’s work, it’s Vernam’s work that truly popularized the one-time pad.

Vernam came up with his idea in 1917 which is from a period I’m going to discuss in the next 2 parts of this series. In particular, I’m going to leave the description of Vernan’s method for part 6 of the series. In that post, the focus is going to be on the first serious attempts to use machines for automating parts of the cryptographic process.

Combinatoric analysis

How secure is the one-time pad?

What if I told you that this is the most secure cipher ever invented? And not just at the time of its invention, but even to this day. You read that right. Even our most advanced ciphers today aren’t as secure.

In fact, the one-time pad is so secure that it’s theoretically impossible to break. Well, as long as you use it properly. That is, as long as the key is truly random and never reused. This was proved by Shannon in that 1949 paper I mentioned in the autokey cipher section: Communication Theory of Secrecy Systems.

I won’t go into his proof here, but the simple intuition for why the one-time pad is impossible to break is that there’s nothing to break. Not just with brute-force, but with any other method. Think about it, what does it even mean to break this cipher?

Let’s say you tried to guess the key with brute-force. Let’s even assume that the ciphertext is only 5 letters long: “wiqnn” coming from the plaintext “hello”. There are possible keys here. It’s a large number but still you could try all of them. The question is, how will you even know that you’ve guessed the right key? Sure, one of the keys will turn “wiqnn” into “hello” but other keys will turn it into other 5-letter words that will be equally likely candidates for the original plaintext.

This isn’t true for other ciphers, since the overwhelming majority of the possible keys will produce nonsensical plaintext and you can easily spot the right key.

Well, given all this, I have no choice but to give this cipher a security score of infinity.

Brute-force security score: ∞

Summary

In today’s post, I talked about the evolution of cryptography throughout the first 19 centuries of the Common Era. I told you that until the 15th century cryptography was evolving more or less independently in Europe and Asia.

The particular focus of the post was on polyalphabetic substitution ciphers. They were first invented by Arab cryptographers in the 9th century and independently by European cryptographers 6 centuries later. The early polyalphabetic ciphers I showed you were invented by Alberti and Trithemius, followed closely by Bellaso and Vigenère.

In the previous post I showed you how the earliest idea of a column cipher in Ancient Greece evolved into more complicated transposition ciphers. Well, in this post you saw how the Caesar cipher itself became the basis of much more complicated substitution ciphers too.

Before I conclude this post, let me give you a summary of all the ciphers I showed you today, along with their combinatoric analyses.

Brute-force security scores

Here’s a list of all the ciphers I showed you, each with its brute-force security score and the formula for calculating it. In the formulas below, N stands for the number of letters in the message and A stands for the number of letters in the alphabet used for writing the message.

• Alberti’s cipher
  • Number of keys formula: —
  • Brute-force security score: 1
• Trithemius’ cipher
  • Number of keys formula: —
  • Brute-force security score: 1
• Bellaso’s cipher
  • Number of keys formula: 
  • Brute-force security score: 8
• The Vigenère cipher
  • Number of keys formula: 
  • Brute-force security score: 9
• The autokey cipher
  • Number of keys formula:
  • Brute-force security score: 9
• The one-time pad
  • Number of keys formula: —
  • Brute-force security score: ∞

---

If you feel confident enough in your understanding of transposition and substitution ciphers and want to learn more about cryptographic codes, continue to part 4 of my series dedicated to this topic!