
Today, I’m going to introduce two ciphers from the dawn of cryptography: the column cipher and the Caesar cipher. These ciphers illustrate some of the first human ideas in the direction of cryptographic thought.
This post is part of my series Cryptography: Historical Intro & Combinatoric Analysis.
The link above will take you to the main series post in which I introduce some basic concepts from cryptography. In that post, I talked about the two main approaches in the field. Namely, codes and ciphers. Well, the focus in the current post is going to be on the latter.
Ciphers hide the meaning of a plaintext by manipulating its individual characters and turning it into a ciphertext. Transposition ciphers do that by changing the order of letters, whereas substitution ciphers do it by replacing the letters with other letters. I also told you that most ciphers have a key – a variable piece of information or instruction known only to the users of a cipher. Here you’re going to have the opportunity to see all these concepts in action.
Part of this series also involves performing a combinatoric analysis of the ciphers. That is, evaluating each cipher’s ability to resist a brute-force attack. I’m going to do this by using concepts from combinatorics like the rule of product and permutations to give each cipher a security score from 1 to 10. If you’re new to combinatorics, you’ll benefit from reading my introductory post on the topic.
The two ciphers I’m going to show you are simple and represent one of the earliest attempts at doing cryptography, even though this term didn’t even exist at the time. They were invented more than 2000 years ago but, with some modifications, remained in use throughout later centuries.
Table of Contents
The column cipher
The column cipher, commonly known as the columnar transposition cipher, is one of the simplest transposition ciphers in existence. Here you simply write the plaintext into rows of a matrix with variable number of columns. You do this by skipping any spaces between the words. This is necessary for the security of the cipher and the spaces are inferred by the recipients of the message.
For example, here’s how you can write “we are surrounded” into a 3-column matrix:
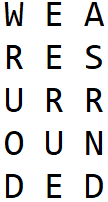
And here’s how you can write the same text into a 4-column matrix:

Notice that here there are only 3 letters in the last row. Often the number of columns won’t divide the number of letters in the plaintext evenly and the last row will be only partially filled. That’s not a problem, as you’ll see below.
There’s a more complex version of this cipher where the matrix columns are also rearranged in some prespecified order. For example, in the 3-column matrix above, we can specify that the order of the columns should be 3-1-2, instead of the default 1-2-3. Then the matrix becomes:

The key of the column cipher specifies the number of columns and their order. In other words, it determines the exact matrix the plaintext is going to turn into. This key is the only thing that needs to remain secret between users of this cipher.
Once you have the plaintext in matrix form, the next step is to create the ciphertext. And when the other side receives this ciphertext, using the same key, they need to put it back in matrix form and then recreate the plaintext. Let’s see how all this works.
Enciphering and deciphering with the column cipher
When the plaintext is in matrix form, to create the ciphertext, you take the columns one by one and write out their letters from top to bottom.
With the 3-column version, the columns are WRUOD, EERUE, and ASRND, so the ciphertext becomes WRUODEERUEASRND. And with the 4-column version, the columns are WERD, ESOE, AUUD, and RRN, so the corresponding ciphertext is WERDESOEAUUDRRN. Finally, with the 3-column version with shuffled columns, the ciphertext is ASRNDWRUODEERUE. Notice that different choices for a key lead to completely different ciphertexts.
To get back the plaintext, the other side first needs to put the ciphertext into a matrix with the right number of rows and columns. Since the number of columns is part of the key (which the other side knows), they only need to determine the number of rows. And the number of rows is simply the length of the ciphertext divided by the number of columns (rounded up, if it doesn’t divide evenly).
Once you know the number of rows and columns, you need to put the ciphertext into a matrix with those dimensions. The first few letters of the ciphertext fill the first column of the matrix. When it’s filled, the next letters fill the second column, and so on. When you enter the whole ciphertext into the matrix, you will have the same matrix that the other side used to encipher the plaintext. For example, the matrix for the ciphertext WRUODEERUEASRND with key 3 is:
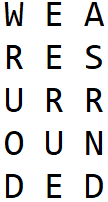
Finally, you can read out the plaintext from the rows.
If you’re dealing with the advanced version of the cipher and the column order is also part of the key, you need to return the columns to their original order before you start reading out the plaintext. Here’s how that works.
Deciphering when columns are shuffled
If the key specifies a column order of 3-1-2 (like in the third example above), you know that the 1st column in the ciphertext matrix should go to position 3, the 2nd should go to position 1, and the 3rd should go to position 2.
There’s a tricky part if you have empty cells in the plaintext matrix. Take the 4-column example above:

If the key specifies a column order of, say, 1-2-4-3, this matrix becomes:

And the ciphertext becomes WERDESOERRNAUUD. If you apply the deciphering procedure above and directly put this ciphertext in matrix form, you will get:
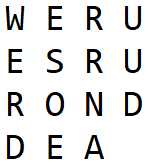
And when you return the columns to their original order (by swapping the 3rd and the 4th columns), you’ll get:
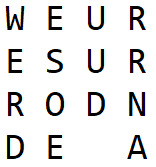
The “plaintext” you will “recover” here is WEURESURRODNDEA (not WEARESURROUNDED). You see it’s quite messed up.
There are two ways around this.
The first is to agree in advance to fill empty cells in the plaintext matrix with random letters. This automatically solves the problem of empty cells. And it will be pretty easy for the recipient to spot and discard the “filler” letters once they decipher the text. The disadvantage is that it makes the cipher less secure because potential eavesdroppers will know that the number of letters in the ciphertext is a multiple of the number of columns used to encipher it.
In the second approach, the recipient calculates the remainder of the division to figure out how many cells in the last row should be empty. In the example above, the number of letters is 15 and the remainder of
is 3. This means that the last row has 3 letters and 1 empty cell. Consequently, the 4th column must also have 3 letters. Knowing this, the recipient must remember to fill the 4th column with only 3 letters and jump to the next column, whatever the 4th column’s position happens to be in the raw matrix (in this case, 3rd).
Historical uses of the column cipher
Now let’s go back in time about… 2500 years! Particularly, to Ancient Greece in the beginning of the 5th century BCE.
This was the end of the Archaic period and the beginning of the Classical period in Greek history. At the time, the territory of Ancient Greece covered territories of present day Greece and (parts of) other countries.
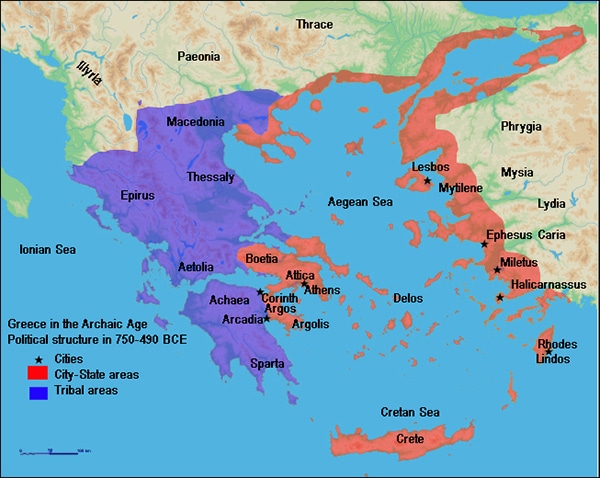
The two most powerful Greek city-states then were Sparta and Athens and there was constant tension and a threat of war between them. However, what caused them to temporarily put their differences aside and unite was an external threat.
Since the middle of the 6th century BCE, the Persian Empire (centered in present day Iran) had been making aggressive territorial gains towards Greece. This eventually led to the Greco-Persian Wars of 499-459 BCE.
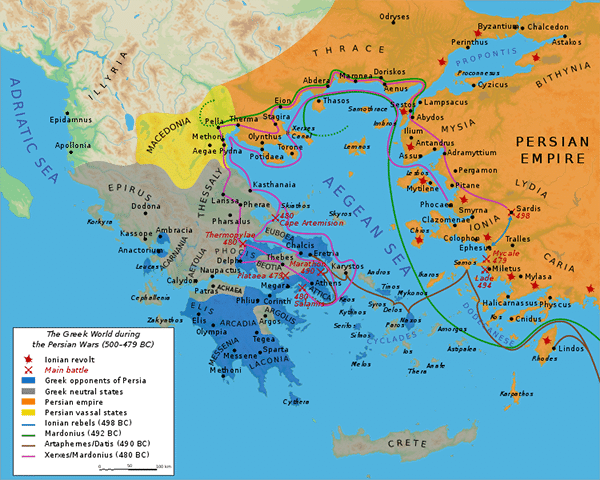
These wars ended with Greek victory and the Persian threat was eliminated. Now that the foreign enemy was gone, the old rivalry between Athens and Sparta came back to focus. This eventually escalated to a great war between them, the Peloponnesian War of 431–404 BCE.
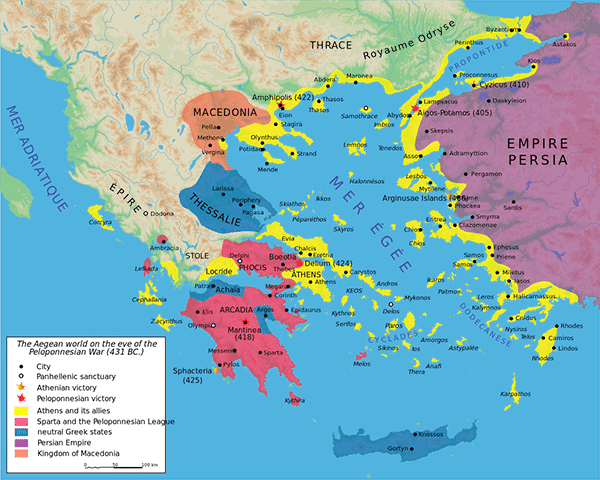
The war was between Sparta and Athens, along with each city’s allies. The two sides were the Peloponnesian League (led by Sparta) and the Delian League (led by Athens).
In a sense, this was a Greek civil war, but the classification is debatable, considering the city-state status of Sparta and Athens. Either way, Sparta turned out victorious and this completely changed the ancient Greek world. Sparta became the leader of all Greeks and Athens never managed to recover its former influence.
The Peloponnesian War is also significant because it might have been the first war where cryptography was used in military communication. The story of this revolves around a tool called “scytale”.
The scytale
The scytale was nothing more than a cylindrical wooden stick. But many historians believe that Spartans used it to encrypt messages in military campaigns during the Peloponnesian War.
They would wrap a thin strap of paper around the scytale without leaving empty spaces and write the message on the resulting “rows”.

Then, they unwrapped the paper and sent it to its intended recipient.
Notice that this produces the exact same ciphertext on the paper that a column cipher would! The letters which end up on top of each other when the paper is still wrapped are like the columns of the plaintext matrix. And similarly, when the paper is unwrapped, they end up next to each other in the ciphertext.
The recipient of the message would wrap the paper around another scytale the same way and read the message row by row. Of course, both communicators had to have scytales with identical diameters. If that’s not the case, the “matrix” that will be formed after wrapping the paper around it would have a different number of columns and deciphering won’t work. In other words, the diameter of the scytale serves the role of the cipher key.
I want to clarify that there is some historical debate whether Spartans really used the scytale as a cryptographic tool or for other purposes. Its earliest mentions as a cryptographic tool are by authors like Apollonius of Rhodes and Plutarch at least 2 centuries after its supposed usage. And the lack of earlier evidence makes some historians question the validity of their accounts.
But even if Spartans didn’t use it for cryptography, we know that at least these later authors were thinking about it in that way, so it still gives us some clue about the timeline of cryptographic ideas’ evolution.
The column cipher after the Spartans
Whenever the column cipher was really discovered, at some point people realized that its most basic version isn’t secure (as you’ll see in my combinatoric analysis below). That’s why throughout the years it was enhanced with the column order shuffling procedure.
Sometimes people also used it in combination with other ciphers, to increase the overall security of the encryption procedures. But at some point cryptographers realized that instead of doing that, they could simply combine the column cipher with itself. That is, apply it twice: once on the plaintext and a second time on the ciphertext they got from the first round of encipherment. Today, this method is commonly known as the double (columnar) transposition cipher.
The double transposition cipher was actually quite popular in the first half of the 20th century. For example, the German military used it in both World War I and World War II (they called it “Doppelwürfel”). During World War II, it was also used by many resistance groups in countries occupied by Germany, like France, the Netherlands, and Czechoslovakia. In the US, the Army and the Office of Strategic Services used it as an emergency cipher. Also, the British Special Operations Executive used it to communicate with its agents.
Enciphering with a keyword
In the 20th century, it was common to specify the key of the column cipher with a keyword. This keyword specifies both the number of columns and their order. The number of columns is determined by the length of the keyword and their order is determined by the rank of the keyword letters in the alphabet. Let me show you how this works with an example.
Suppose you want to encipher “we are surrounded” with the keyword “duck”. The first thing you do is put the plaintext in a 4-column matrix (because “duck” has 4 letters) and write the keyword on top of the matrix:

Then you reorder the columns so that the letters of the keyword are in their proper alphabetical order:
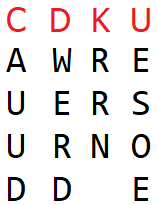
And then you create the ciphertext from the columns of this matrix. The receiving side needs to perform the opposite operations to get back the plaintext. This is pretty much the same procedure I described in the previous sections, just maybe a little more intuitive to implement.
Notice that, to avoid ambiguity, the keyword should not have the same letter repeated more than once.
Combinatoric analysis of the column cipher
Breaking this cipher means figuring out its key. Let’s start with the simplest version where the key only specifies the number of columns of the matrix.
A brute-force attack on the column cipher means individually trying every possible key. So, if we intercept a ciphertext whose length (number of letters) is N, how many possible columns could it have been enciphered with?
Well, think about. The number of columns can’t be 1, since that would just produce the original plaintext. For the same reason, it can’t be N (or greater than N) either. But all other choices for a key will produce unreadable ciphertext. So, the candidate key values are all the numbers between 1 and N (excluding the boundaries):
Therefore, the possible number of keys here is:
Alright, that’s not very secure, is it? Even if the ciphertext is very long, say 1000 letters, that means there are only 998 candidate keys. And yes, trying all 998 keys can be long and tedious, but it’s doable. Especially with current technologies. This isn’t secure at all.
Brute-force security score: 2
What if columns are shuffled?
How can we calculate the combinatoric complexity of the advanced version of the cipher where the column order is part of the key?
Here’s how it works. Any given key is associated with a specific number of columns, right? Let’s denote the number of columns with the letter k. How many different column orders are there for a particular k?
In combinatorics, a particular order of a certain number of objects is called a permutation. As I explained in my introductory post on combinatorics, the total number of permutations of k objects is equal to k! (k-factorial).
Okay, so there are k! possible permutations (orders of the columns) for each k. Therefore, to calculate the number of all possible keys, we need to sum these factorials over all k, ranging from 2 to N:
Notice that this time we’re summing from 2 to N (not N – 1) because changing the order of the columns allows you to create proper ciphertext even if the number of columns is equal to the length of the text.
By the way, if you’re not familiar with the sum operator (the above notation), please take a look at my post about this notation.
Anyway, is this version of the cipher secure? Let’s take a short message like “we are surrounded”, which is 15 letters long. If you set N = 15 in the formula above, you get:
That’s a pretty high number (almost 1.5 trillion)! Obviously, no hand method will be able to crack the key here. Still, a brute-force attack is more than possible with today’s computers. But for even moderately longer messages, the number of keys becomes impossible to be handled with brute-force attacks.
Brute-force security score: 8
What if double encipherment is used?
Finally, let’s analyze the double transposition cipher used in the 20th century.
First, let’s consider the case without column shuffling. Here the final key consists of two parts, where each part has N – 2 possible keys. That’s because the length of the final ciphertext will still be the same as the length of the plaintext. If we consider the two-part composite key, how many possibilities are there now?
Let’s see. There are N – 2 possibilities for the first step and another N – 2 for the second. Every possible key from the first step can be combined with every possible key from the second step. Then, this is nothing but a straightforward application of the rule of product:
(I explained the rule of product in my introductory combinatorics post and reminded you about it in the introductory post of this series).
This still isn’t very secure, but at least it might significantly slow down anybody trying to break the cipher by hand with a pen and paper.
Brute-force security score: 3
Double encipherment and shuffled columns
If we also use column shuffling, another straightforward application of the rule of product gives us:
Is this secure? Actually, it is. For a ciphertext of length 15, the number of possible keys is:
That is pretty large! And the situation gets much worse for longer ciphertexts.
I’m going to give this most sophisticated version of the cipher a score of 9. It’s not 10 because for very short messages (15 or fewer letters) breaking it with a brute-force approach is possible (though extremely hard). This can be done with the help of some modern supercomputers which are capable of executing hundreds of quadrillions (about ) of operations per second.
Brute-force security score: 9
The Caesar cipher
The Caesar cipher is one of the most famous substitution ciphers. Not so much because it’s a great cryptographic tool (it’s not, especially today), but for historical reasons.
This is also one of the simplest monoalphabetic substitution ciphers out there. Here’s how it works.
To turn a plaintext into a ciphertext, you simply shift each letter of the ciphertext by N letters down the alphabet. N is a number between 0 and 25, assuming we’re dealing with the standard Latin alphabet of 26 letters. For example, if you encipher the word “hello” with a shift of 1, H becomes I, E becomes F, and so on. And the final ciphertext becomes “ifmmp”.
If the letter rank + the shift is more than the length of the alphabet, you simply continue counting from the beginning of the alphabet. For example, the letter Z with a shift of 1 becomes A, with a shift of 2 it becomes B, and so on. In other words, here you’re using simple modular arithmetic.

This cipher got its name from Julius Caesar. By accounts of some of his contemporary historians, he was using it with a shift of 3 when he wanted to send secret letters.
Caesar was a Roman military general and politician who probably needs little introduction. He was one of the most powerful and influential people who ever lived. Caesar played a central role in the eventual end of the Roman Republic and the birth of the Roman Empire.
Now let’s take a look at the details of using this cipher and then I’ll apply it to some actual letters of Caesar where he might have used it himself.
Enciphering and deciphering with the Caesar cipher
A simple device you can use to encipher and decipher with Caesar ciphers (and other shift ciphers) is the tabula recta (I’m going to tell you about its invention in the next post of the series). This is a 26 by 26 grid where each row represents the alphabet shifted by a number between 0 and 25:
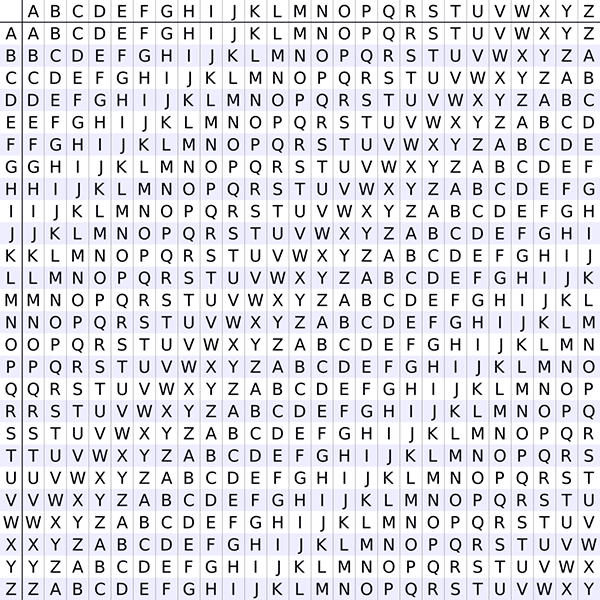
The leftmost column is for specifying the key (the shift). For example, the letter A corresponds to a shift of 0, the letter D to a shift of 3, and so on. And the topmost row is the reference point for your plaintext letters.
To encipher a message, you draw lines from the plaintext letters in the top row to the corresponding letters in the row of your key. The matching letters become the ciphertext substitutes.
For example, let’s encipher “we are surrounded” with the key G. The unique letters in the sentence are A, D, E, N, O, R, S, U, and W. After the shift, these letters are respectively substituted with G, J, K, T, U, X, Y, A, and C from the G row.
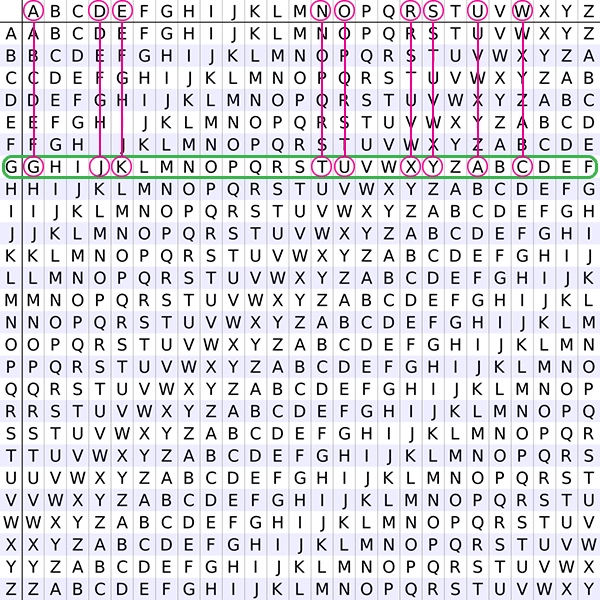
And the corresponding ciphertext becomes “ck gxk yaxxuatjkj”.
Deciphering works in the opposite direction. If you know that a message was enciphered with a shift of 6, you apply a shift of negative 6 to the ciphertext to get back the plaintext. Or, alternatively, you can apply a shift of 26 – 6 = 20 to get the same result (again, this is just modular arithmetic).
Now, just for fun, let’s use the Caesar cipher to encipher a few letters from Caesar himself.
Keep in mind, we don’t know which of his letters Caesar actually enciphered. But given the nature of the subject, we can assume that he would probably have wanted to send the following letters in secret.
Caesar’s use of his cipher
Before showing you the letters, let me first give a little bit of historical context, so you can better understand their contents.
Caesar’s ascent to power
Caesar was born in 100 BCE. From an early age he began pursuing political and military ambitions.
Long story short, in 60 BCE (at the age of 40), he formed a semi-secret alliance with Pompey and Crassus, who were two of the most powerful people in the Roman Republic. Historians call this alliance the First Triumvirate. A year later, Caesar was elected consul for one year. At the time, this was the most powerful position in the Roman Republic.

Shortly after his consulship, Caesar began a military campaign for 8 years, now called the Gallic Wars, during which he conquered the region of Gaul. This was a huge expansion of territory for the Roman Republic. The region of Gaul occupied the territories of present day France, Luxembourg, Belgium, and Switzerland, as well as parts of Germany, the Netherlands, and Italy.
The First Triumvirate fell apart shortly after the death of Crassus in 53 BCE. Tension and rivalry started growing between Caesar and Pompey. It was never a very stable allience in the first place because the interests of the three men were aligned only temporarily.
After the huge military success in the Gallic Wars, Caesar gained large popularity among common people. This made the Roman Senate and Pompey worried about his power ambitions.
The Senate decided to side with Pompey (who had been a consul in 52 BCE). That’s why in 50 BCE they ordered Caesar to disband his army and return to Rome. Instead, in January 49 BCE, Caesar marched one of his legions to Rome. This act started a 4-year-long civil war which Caesar eventually won and assumed the position of dictator of the Roman Republic.
Caesar’s letters during the Great Roman Civil War
After Caesar approached Rome with his army in 49 BCE, Pompey decided to consolidate his own army in the South of Italy and retreated to the city of Brundisium. He asked his ally Domitius to meet him there so they can join forces. However, before he can do so, Caesar’s forces trapped Domitius around the city of Corfinium where he had to surrender. Still, Caesar didn’t punish Domitius and instead set him free hoping he would be able to convince Pompey to agree to peace terms.
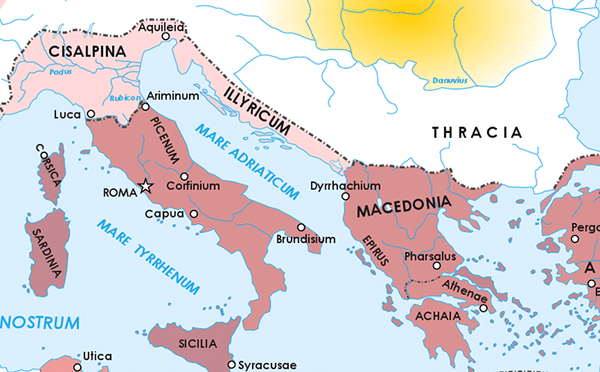
Shortly after that, Caesar also tried to trap Pompey in Brundisium but Pompey managed to escape to the Epirus province through sea.
In March of 49 BCE, about 2 months into the war, Caesar wrote two letters to his friends and allies Oppius and Cornelius about these events. Both of them were big opponents of the war and had been actively trying to make Caesar and Pompey settle their differences peacefully.
First letter to Oppius and Cornelius
Here’s the first letter, as it might have been written in Caesar’s ciper with a shift of 3 (that is, with the key D):

Obviously, you don’t understand anything. Well, after all, it’s enciphered and you’re not supposed to! So, let’s apply a shift of negative 3 to see what Caesar wrote:

Okay, this is in Latin and I don’t imagine most of you speak this language (neither do I). Luckily, the English translation is also available to us:

Second letter to Oppius and Cornelius
Now let’s look at the second (“original”) letter:

Here’s the deciphered version in Latin:

And here’s the English translation:

A letter to Cicero
After Pompey’s escape in March, Caesar marched to destroy his forces in Hispania. Which he did in less than a month. On his way to Hispania, he sent a letter to Cicero.
Cicero was a powerful figure in the Roman Republic (also an ex-consul). During the civil war, both sides had tried to win his allegiance, but he refused to take part in the conflict. Instead, he remained neutral and tried to compel them to make peace.
However, due to some rumors at the time, Caesar worried about his neutrality and wrote this letter to ensure Cicero doesn’t join Pompey:

In Latin, the letter says:

And here’s the English translation:

I don’t know about you, but reading these original letters with their historical context truly fascinates me.
Well, Cicero ended up maintaining neutrality (kind of). After the war, the situation between him and Caesar was cleared and Caesar pardoned him for his lack of support.
Combinatoric analysis of the Caesar cipher
The Caesar cipher has only 26 possible keys. In general it has A possible keys, where A is the number of letters in the alphabet used to write the message.
Some alphabets may be much longer than the Latin alphabet and may have a 2-3 times larger value for A. But even with them it would be trivial to individually check all the keys.
Therefore, this cipher lacks any security.
Brute-force security score: 1
But let’s not leave the analysis here. Since this is the first monoalphabetic substitution cipher of this series, let’s also consider the combinatoric complexity of a more general monoalphabetic substitution cipher.
A general monoalphabetic substitution cipher
If all we know about a ciphertext is that it was generated with a monoalphabetic substitution cipher, we can view it like the letter substitution rule I showed in the introductory post:

This, of course, is only one possible substitution rule. Imagine the key of the cipher is the particular mapping between letters (like the one above). Any other substitution rule would be a different key.
In cryptographic literature, this cipher commonly goes by the name simple substitution cipher.
To correctly guess which rule was used with a brute-force approach, you need to check all possible such rules. But how many of them are there?
Well, take a look at the image above. The letters on the left of the arrows are listed in their proper alphabetical order, whereas the ones on the right are a random shuffle of the same letters. To figure out how many rules are possible, you basically need to figure out the number of ways in which you can order the letters on the right. Which means, the number of ways to order the letters in the alphabet.
In other words, you need to calculate the number of permutations of all letters. If A stands for the number of letters in the alphabet, the number of possible keys here is simply:
For the Latin alphabet, this number is:
That’s not bad! This number is close to the number of keys for the double transposition cipher when the message is about 15 letters long. Obviously, no hand method will be able to crack the key. But you can still guess the right key with the help of supercomputers, so I’m giving the simple substitution cipher a score of 7.
Brute-force security score: 7
Overview of cryptography before the Common Era
In this post I showed you two of the earliest ciphers in human history. In the next posts of this series, the focus is going to be on more recent cryptography. So, before we move on, let me give you a rough overview of the state of cryptography before the Common Era.
Well, at the time cryptography was almost nonexistent. The earliest attempts to conceal the meaning of written text were more about creating mystery or amusement than to ensure secrecy of communication.
For example, archaeologists have found unusual hieroglyphs (substituting regular ones) carved into the walls of a tomb in an ancient Egyptian town called Menаt-Khufu in the 20th century BCE. Take a look at a few examples (the unusual hieroglyphs are on the left of the “equals” sign and their real meaning is on the right):

Some slightly more serious attempts at cryptography were made in places like India and Mesopotamia between the 16th and 3rd centuries BCE, where people were exploring very basic forms of substitution ciphers.
Also, Hebrew scholars were using a substitution rule called Atbash around the 7th century BCE where the letters were substituted with the alphabet in reverse. For example, if you applied Atbash to the Latin alphabet, the substitution rule would be A -> Z, B -> Y, C -> X, D -> W, and so on. In other words, this is a special case of the simple substitution cipher with no key.
Greek and Roman cryptography
Then, of course, Ancient Greeks and Romans were also making sporadic attempts at cryptography from around the 5th century BCE. I already showed you two of those attempts here. But they weren’t the only ones. There is some historical evidence that other Romans like Cicero and Augustus also used some basic methods for concealing messages.
In Greece, in the 2nd century BCE, the historian Polybius developed a method now called the Polybius square. This was a 5 by 5 grid where the letters of the (Greek) alphabet were written in order. The rows and columns were labeled with the numbers from 1 to 5:
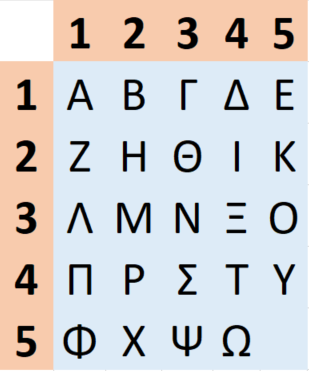
The Polybius square was intended to be used as a simple substitution rule where each letter was substituted with a combination of its row and column numbers. For example, the letter Γ is written as 1-3 (or just 13), the letter Σ as 4-3 (43), and so on.
As you can see from all these examples, in those days cryptography wasn’t very advanced. Well, before the Common Era even writing itself was an extremely rare ability. Just putting some words in written form was already a high enough security measure against most eavesdroppers. Probably for that reason the need for cryptography wasn’t too high to begin with.
But at least you have a good sense of how things were before the Common Era. Now you’re ready to delve into more recent cryptographic methods!
Summary
I told you that cryptography is divided roughly into codes and ciphers. The focus of this post was on the latter. Since ciphers themselves can be transposition and substitution ciphers, I introduced you to one of the earliest examples from each category.
The column cipher is a prime example of a transposition cipher. It was (probably) invented by Spartans in the 5th century BCE. Or at least by other people some time in Ancient Greece. And, in one form or another, it remained in use until the second half of the 20th century. This cipher involves putting a plaintext into matrix form with the number and order of its columns specified by the cipher key. The ciphertext is then created by joining the columns of the matrix. Deciphering works in the opposite direction, by first putting the ciphertext in the appropriate matrix form (using the same key) and joining its rows.
I also told you about the double transposition cipher which is simply applying the column cipher twice.
The other cipher I showed you is the Caesar cipher. This is one of the oldest monoalphabetic substitution ciphers and was (probably) invented by Julius Caesar in the 1st century BCE. It involves simply shifting each letter in the plaintext by a constant number between 0 and 25 (assuming it’s written in the Latin alphabet). This number is the key for the Caesar cipher. Deciphering works by applying a negative shift with the same key. As far as we know, nobody besides Caesar used this cipher for any serious purpose.
But the Caesar cipher became the basis for more complicated ciphers. I’m going to show you three of these ciphers in the next post of this series. Namely, the Vigenère cipher, the autokey cipher, and the one-time pad.
Brute-force security scores
I showed you how to calculate the number of possible keys for each cipher. Most of it involved simple counting and/or a simple application of the rule of product. And the formula for permutations, which of course is also based on the rule of product.
Here’s a list of all the cipher variations I showed you, each with its brute-force security score and the formula for calculating it. In the formulas below, N stands for the number of letters in the message and A stands for the number of letters in the alphabet used for writing the message.
- Column cipher (fixed column order)
- Number of keys formula:
- Brute-force security score: 2
- Number of keys formula:
- Column cipher (variable column order)
- Number of keys formula:
- Brute-force security score: 8
- Number of keys formula:
- Double transposition cipher (fixed column order)
- Number of keys formula:
- Brute-force security score: 3
- Number of keys formula:
- Double transposition cipher (variable column order)
- Number of keys formula:
- Brute-force security score: 9
- Number of keys formula:
- Caesar cipher
- Number of keys formula: A
- Brute-force security score: 1
- Simple substitution cipher
- Number of keys formula:
- Brute-force security score: 7
- Number of keys formula:
If you’re curious to see how cryptography continued to develop after the Common Era and learn about polyalphabetic substitution ciphers, check out part 3 of the series!
![Rendered by QuickLaTeX.com \[ \textrm{\# keys} = \sum_{k=2}^{N} k! \]](https://www.probabilisticworld.com/wp-content/ql-cache/quicklatex.com-9dc8e7ff574cd998b4169e37d474b03c_l3.png)
![Rendered by QuickLaTeX.com \[ \sum_{k=2}^{15} k! = 1401602636312 \approx 1.5 \cdot 10^{12} \]](https://www.probabilisticworld.com/wp-content/ql-cache/quicklatex.com-82cf8beff0af95798858967198f97dbf_l3.png)
![Rendered by QuickLaTeX.com \[ \textrm{\# keys} = \sum_{k=2}^{N} k! \cdot \sum_{k=2}^{N} k! = \left(\sum_{k=2}^{N} k! \right)^2 \]](https://www.probabilisticworld.com/wp-content/ql-cache/quicklatex.com-65d095aa5ca6533b00811439e2a622d3_l3.png)
![Rendered by QuickLaTeX.com \[ \left(\sum_{k=2}^{15} k! \right)^2 = 1964489950116748540961344 \approx 2 \cdot 10^{24} \]](https://www.probabilisticworld.com/wp-content/ql-cache/quicklatex.com-c80e2ec47da8d2fbfb3c0e64702c9ee2_l3.png)
Leave a Reply