The Birth and Evolution of Cryptographic Codes

Welcome to part 4 of my series on cryptography! After taking an in-depth look into ciphers in the previous two posts, now it’s time to delve into the other big category of cryptographic methods. So, this week’s post is going to be about cryptographic codes.

This post is part of my series Cryptography: Historical Intro & Combinatoric Analysis.

Let’s remember the big picture of cryptography:

• Ciphers
  • Transposition ciphers
  • Substitution ciphers
    • Monoalphabetic ciphers
    • Polyalphabetic ciphers
• Codes

In part 2 of this series, I talked about ancient cryptography and showed you two of the earliest transposition and monoalphabetic substitution ciphers (the column cipher and the Caesar cipher). And in part 3 I showed you many examples of polyalphabetic substitution ciphers (most notably, the Vigenère and autokey ciphers, as well as the one-time pad).

By now, you must have a good understanding of the evolution of ciphers (and cryptography in general) up until the 20th century. One thing that I haven’t touched upon is cryptographic codes for the same period. Well, the goal of this post is to fill this missing gap.

Overview of the post

In the sections below, I’m going to show you how the concept of cryptographic codes was discovered and how it developed over the centuries, up until the 20th century.

In the next post I’m going to introduce more codes when discussing World War I cryptography, where they played a very important role. After World War I, procedures improved and codes remained in use until the end of World War II (and, more sporadically, in the following two decades). But after World War I, a process of replacing codes with more sophisticated methods had begun.

In the sections below I’m going to present some famous codes, show you their details, and give you historical context around their invention and usage:

• Alberti’s code
• The nomenclator (particularly, the code of Mary, Queen of Scots)
• The route cipher
• Baravelli’s code

And, as always, I’m going to analyze the security of each code with a combinatoric analysis of their resistance to brute-force attacks.

After reading this post, you’ll have an almost complete picture of cryptography’s development until the 20th century. I’m going to fill the few remaining gaps by the end of the series, even though the focus there is going to be mostly on 20th century cryptography.

The first codes

The first codes were very simple and, by modern standards, very insecure. In fact, it seems like initially their purpose was often more to shorten messages, rather than to make them unreadable.

In the previous post, I briefly mentioned the 11th century Chinese military collection Wujing Zongyao which recommended a small code for military communication. Very primitive codes were also used in the Vatican by different popes and cardinals from around the 14th century where they replaced some common words with single capital letters (A = king, D = the Pope, etc.).

These codes were very immature and, by today’s standards, offered no real security. Well, they offered very little security even for the standards of earlier periods. So, let me show you one of the first solid codes that had real cryptographic security.

Alberti’s code

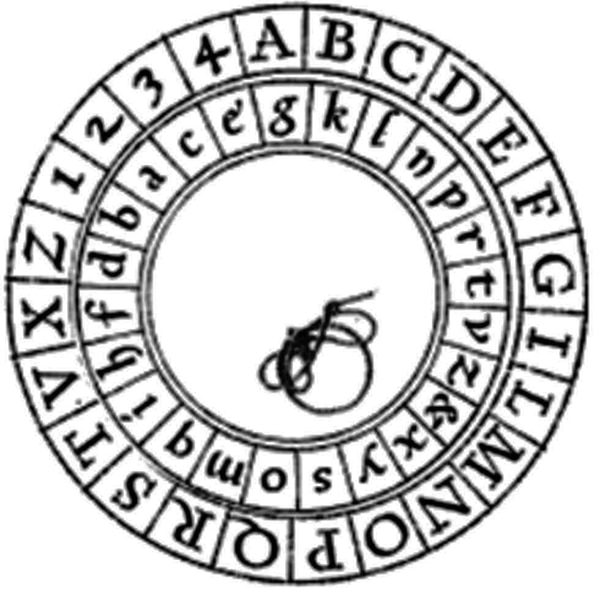
Do you remember Alberti’s cipher disk from the 15th century I showed you in the previous post? There I told you that it was a tool for implementing one of the first polyalphabetic ciphers in history. What I didn’t tell you was that it was also a tool for one of the first cryptographic codes.

Encoding was done with the four digits which were part of the plaintext alphabet (the symbols on the large circle). Alberti combined them into two-, three-, and four-digit groups to create a total of 336 combinations:

   

And each group (like 11, 243, 3341, etc.) stood for a particular word or a phrase. The code-meaning associations were written in a table which served the role of a codebook. One of the examples Alberti himself gives is:

In this table, according to agreement, we shall enter in the various lines at the numbers whatever complete phrases we please, for example, corresponding to 12, ‘We have made ready the ships which we promised and supplied them with troops and grain.’

Just like any other plaintext, Alberti recommended enciphering these code words with his polyalphabetic cipher as well. This was the first European example of superencipherment (I’ll tell you more about that in the next sections).

The nomenclator

In the previous post, I showed you how in Europe polyalphabetic substitution ciphers were invented in the 15th and 16th centuries. But the main example of a serious use I gave you was the Vigenère cipher during the US Civil War in the 1860s. Why the big gap?

Well, the short answer is that people simply found polyalphabetic ciphers hard to use and prone to error. Until the invention of the telegraph in the 19th century, another cryptographic system was the most popular: the nomenclator.

The name “nomenclator” comes from an early meaning of a person whose job is to remember information like names of people and later it became associated with books for keeping similar information. And, in the context of cryptography, nomenclators were the first codebooks.

This was a system that combined both codes and ciphers. Which was kind of similar to Alberti’s method, except it used monoalphabetic substitution and didn’t use superencipherment. It involved enciphering most of the plaintext as usual but replacing certain common words with specific symbols or code words, instead of regular ciphertext.

Two other inventions associated with nomenclators were the concepts of homophones and nulls. Homophones were alternative substitutions for particular high-frequency letters. Meaning, some high-frequency letters (like ‘a’, ‘e’, and ‘t’) had multiple substitutes, instead of just one. On the other hand, nulls were ciphertext symbols that didn’t stand for any plaintext letter and were there just to confuse potential eavesdroppers (they were supposed to be skipped during deciphering).

Nomenclators were widely used between the 14th and 19th centuries in many European countries like Italy, Spain, England, and France.

History of the nomenclator

The first nomenclator was a compilation of ciphers from the beginning of the 14th century by Gabriele de Lavinde of Parma, one of the secretaries of Antipope Clement VII. It contained a set of keys that combine a monoalphabetic substitution alphabet (with nulls) and a short list of a few dozen common words or names with two-letter code equivalents. This was extended by other Italians to include homophonic substitution and larger lists of codewords. They improved the procedures by removing spaces and punctuation from the ciphertext and sometimes even used polyphones (ciphertext symbols with more than one plaintext meanings).

Nomenclators were further developed in Spain in the 16th and 17th centuries, starting from the reign of Philip II. Homophonic substitution was now used not just for single letters but for common two- or three-letter combinations. The code section started growing to more than 1000 words.

One common characteristic of most nomenclators was that the codes and their corresponding meaning were both arranged in alphabetic/numeric order. For example, if the code words are numbers, the lowest numbers represented words starting with A and the highest numbers represented words starting with Z. This practice was for convenience but it was also a security weakness.

This weakness was fixed in the 17th century by the famous French cryptographer Antoine Rossignol. He introduced the so-called two-part nomenclator where the alphabetic order of words was random relative to the order of codes. To keep the convenience aspect, nomenclators had two lists — one where the words are listed alphabetically but the code order is random and vice versa.

Nomenclators continued to be used in many places in the 18th century and the beginning of the 19th century. Substitution rules were becoming more complex and the code sections could be up to 3000 words.

The nomenclator of Mary, Queen of Scots

I want to show you a real example of a nomenclator which also has a pretty interesting story behind it. This is the nomenclator used by Mary, Queen of Scots.

Mary was a queen of Scotland in the 16th century and historians describe her as smart, beautiful, and talented. Sadly, she also had a tragic end.

Mary was queen of Scotland from 1542 (her birth) until 1567 when she was forced to abdicate and was imprisoned by her own people. The reason was suspicions that she had plotted the murder of her husband. A year later, she managed to escape and ran to England to seek help from her cousin, queen Elizabeth I. Unfortunately, Elizabeth, perceiving her as a threat, chose to imprison her instead.

Mary spent the following 19 years under a sort of a house arrest in an English castle under the supervision of Sir George Talbot. She was allowed to have some domestic staff but her overall living conditions weren’t too good. Also, she wasn’t allowed to have any correspondence with the outside world.

Mary’s codes

Mary managed to overcome the last obstacle by finding a secret way to smuggle letters in and out of the castle. The person facilitating this was Gilbert Gifford. He was one of the few people Mary was allowed to see during her imprisonment and he was delivering her messages by hiding them inside the stopper of a beer barrel.

As an extra security measure, she was using different codes to encipher her messages. Here’s a preserved copy of one of those codes (click on the image to see a larger version):

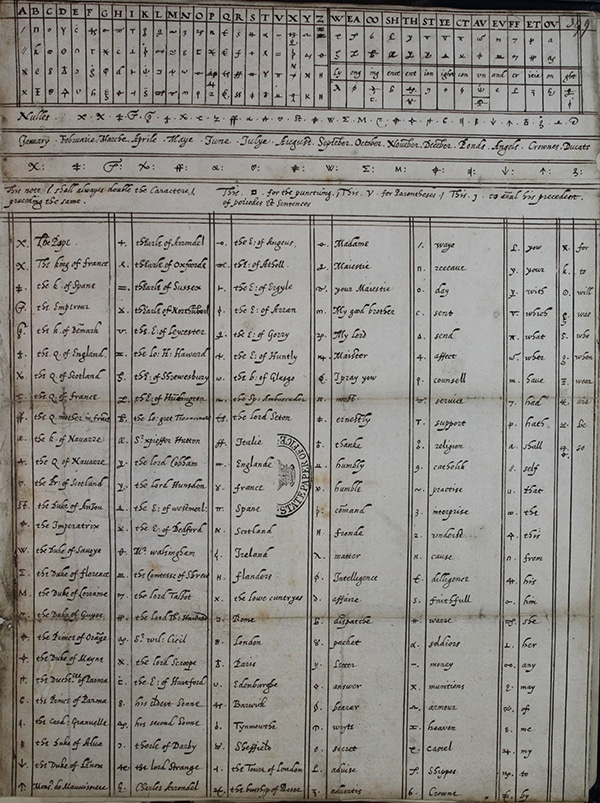
This is a fascinating document, so let’s analyze it.

It’s roughly divided into 5 sections:

• A homophonic substitution table for letters (top left)
• A homophonic substitution table for common letter combinations (top right)
• A list of nulls (right below the two tables)
• A list of code symbols for common units like months and currency (right below the nulls)
• A table of code symbols for common words and expressions like “Madame”, “The Pope”, and “The King of France” (bottom)

As you can see, this nomenclator uses mostly random symbols (instead of letters) as substitutes. This was a common practice in that period. Mathematically, it doesn’t make the ciphers more secure, but it might be able to confuse some inexperienced codebreakers.

Here’s one of the last codes that Mary used (unfortunately, the quality isn’t as good, but it’s still somewhat readable):

Here’s a more readable version of part of it (source):

Mary used the above code to write her last letter to Sir Anthony Babington during the infamous Babington Plot, which ended up getting her executed.

The Babington Plot

You might be wondering why Elizabeth decided to imprison Mary in the first place. After all, they were cousins, weren’t they? Not to mention, there was never concrete proof that she took part in her husband’s murder (she probably didn’t).

You see, at the time England was transitioning from Catholicism to Protestantism, following the wave in Europe caused by the Reformation. Queen Elizabeth I was a protestant, whereas Mary was a catholic. Not only that, Mary had a legitimate claim to the English throne which she had previously tried to push. At the time, the country itself was split between the two religions and a significant part of the catholic population supported Mary’s claim (hoping she would restore Catholicism in England). All of this convinced Elizabeth that it’s safer to keep Mary imprisoned.

Sir Anthony Babington was one of those Catholics who wanted to help Mary replace Elizabeth as queen of England. In 1586, along with other conspirators, he plotted to assassinate Elizabeth, rescue Mary, and make her queen. The last part of the plan was supposed to be achieved with military help from Spain and France who didn’t switch to Protestantism and were trying to stop its spread in Europe. All this was happening during the reign of Philip II in Spain whose use of nomenclators I mentioned in one of the previous sections.

Mary was an active participant in the plot. Her participation was happening through messages she was secretly sending and receiving from her castle. Unfortunately for her, the plot was doomed to fail, since it was discovered by Elizabeth’s spies from the very beginning. This eventually led to the arrest and execution of all participants, including Mary herself.

Mary’s last letter during the Babington Plot

During the plot, Mary and her two trusted secretaries exchanged a few letters with Babington.

What Mary didn’t know was that Gifford (her messenger) was in fact a double agent working for Elizabeth’s spymaster Sir Francis Walsingham. Sir Francis was using the abilities of a talented linguist and cryptographer, Thomas Phelippes, to decipher and read Mary’s letters as soon as they were sent or received. So, the whole plot was being monitored and it never had a chance of succeeding. Sir Francis let it continue in order to give Mary a chance to incriminate herself with her letters and use this as a reason for her execution.

In his last letters, Babington outlined the details of the plot, including the part where “six gentlemen” were going to assassinate queen Elizabeth. In her reply, Mary tentatively agreed with the plan and this was sufficient for her incrimination. Now Sir Francis was ready to shut down the plot and arrest anybody involved. To do that, he asked Phelippes to forge a postscript to Mary’s letter (using her own cipher!), “asking” Babington to reveal the names of the six men who were supposed to carry out the assassination.

Lucky for us, this forged postscript has been preserved:

It was enciphered with the second code I showed you in the previous section. If you like, try to decipher it yourself, though this won’t be an easy task because of the poor quality of the letter combined with the old spelling.

Anyway, here’s what the text says:

Mary’s full letter was quite long. If you’re curious to read it, here’s a link. It’s from the 19th century history book Mary Queen of Scots and the Babington Plot (now in the public domain).

Overview of codes in the 19th century

The late 18th and early 19th centuries were the beginning of a revolution in communication technologies. The most notable invention, of course, was the telegraph. And as communication became more efficient, this also increased its importance in many areas of life, including warfare. Well, especially warfare!

No longer could a general sit horseback atop a hill and survey the battle, like Napoleon or Hannibal, sending messengers to hand-carry instructions to wheel or to counterattack. The forces engaged were too numerous, the field too vast. He had to work from a command post far in the rear, following the progress of the battle by telegraph on maps that showed more than his naked eye could ever see. He could issue orders by telegraph that would coordinate the movement of one out-of-sight wing with that of another, bring up reserves to block an enemy charge, order up food and ammunition in a hurry. The number of messages grew correspondingly. The command post became virtually a communications center.

David Kahn, The Codebreakers

Since nomenclator’s invention in the 14th century, its variations remained popular across the world until the 19th century. But now that communication was becoming so important, so was communication’s secrecy. And people started realizing the nomenclator was simply not good enough to meet these new secrecy requirements.

The nomenclator wasn’t secure enough mainly because it was still relying on monoalphabetic substitution. And, by the 19th century, codebreakers had excelled in breaking it, despite security features like nulls and homophones. So, in the late 18th and early 19th centuries, cryptography gave up on the nomenclator and began improving in 2 separate directions:

• Polyalphabetic ciphers
• Cryptographic codes

The birth of modern cryptographic codes

In the previous part of the series, I told you about the use of polyalphabetic ciphers (namely, the Vigenère cipher) by Confederates during the American Civil War of 1861-1865. Polyalphabetic ciphers remained in use ever since but I’ll tell you more about their development in the next 3 parts of the series.

Codes, on the other hand, are an extension of nomenclators in a different direction. Instead of replacing only some of the words with codewords (and enciphering the rest with monoalphabetic substitution), here you replace most or all words with a symbol. These symbols are written in a codebook with tens (or even hundreds) of thousands of entries. Also, these symbols could replace smaller or larger pieces of text (like parts of words, word combinations, or full sentences).

Some ideas in this direction had started appearing even by the end of the 18th century. For example, the (infamous) American military officer during the American Revolutionary War Benedict Arnold came up with a way to encode messages by replacing every word with a sequence of three numbers: page, line, and word. The idea was to share a specific book and use the three numbers for indicating specific words from it. For example, 177-9-4 stands for “page 177, line 9, word 4”. Arnold used this code for secret communication with the British military.

By the middle of the 19th century, the telegraph was becoming a central means of communication and people were inventing different procedures for working with it. One of those was the Morse code, an efficient way of encoding letters and numbers with dots and dashes (represented by short and long telegraph signals).

Francis Smith’s code

The Morse code itself wasn’t a cryptographic tool. But one of the first proper codes was invented by Francis Smith, a business partner of Samuel Morse (the inventor of the Morse code). Smith published a book called The Secret Corresponding Vocabulary: Adapted for Use to Morse’s Electro-Magnetic Telegraph. This is one of the first real codebooks in history. It had 56 thousand entries listed in alphabetic order. As an example, here’s the first page of the codebook (source):

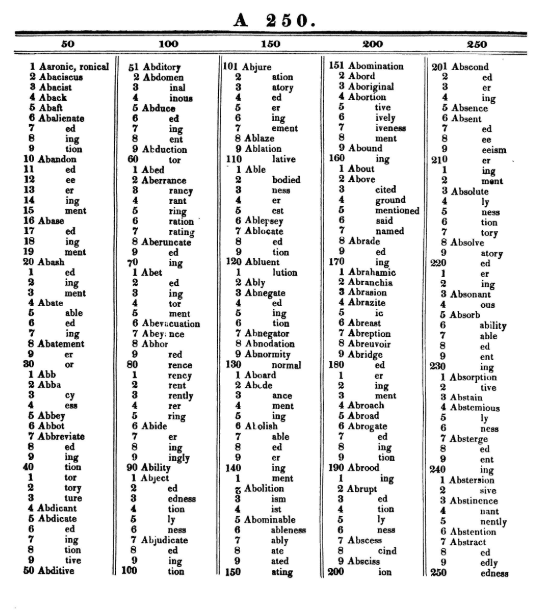
The codebook is divided into chapters for each letter in the alphabet and the numbers in each chapter start from 1. Users were supposed to look up each word in their message in the codebook and replace it with a code block having its starting letter and its number. For example, the word “Abolition” becomes A-142.

You might be wondering if this procedure is that secure. After all, the words and their numbers are both listed in the proper order, which was a problem fixed even in late nomenclators. On top of that, you’re revealing the first letter of each word, which is a lot! Not to mention, anybody who has a copy of the codebook will be able to decipher your messages.

Well, Smith’s solution involved the process of superencipherment. I already mentioned this in the section about Alberti’s code in the beginning. Essentially, superencipherment means using some cipher to encipher the code symbols themselves. In the book, Smith suggests using monoalphabetic substitution for the letter part and adding/subtracting arbitrary values for the number part of each code word (but he also said that users can come up with more complicated ciphers, if they want to).

In the context of superencipherment, the raw code is called placode and the enciphered code is called encicode (analogous to plaintext vs. ciphertext).

Improvements on Smith’s code

Smith’s pioneering work inspired hundreds of commercial codes. They were improving the procedure by introducing larger vocabularies and including higher and higher number of full phrases (besides individual words). Superencipherment itself was becoming more sophisticated too.

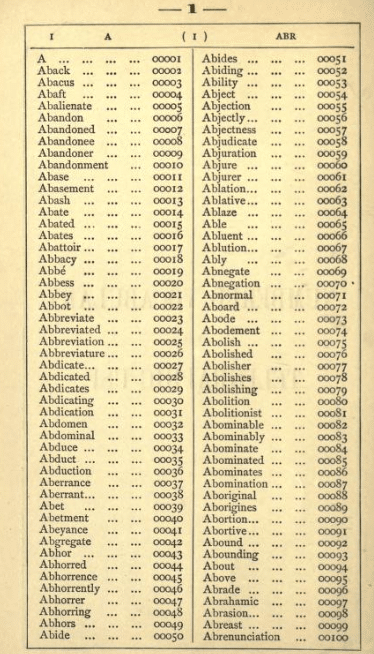
Other codebooks started using real words for code words, instead of random letter/number sequences. The goal was to improve readability, as this by itself doesn’t affect the security of the code.

One well-known codebook was Robert Slater’s Telegraphic Code, to Ensure Secresy in the Transmission of Telegrams from 1870. It had “only” 25 thousand entries but used more secure superencipherment.

Slater described different types of complex transforms of the number codes, like regrouping the digits or changing their order. But he also didn’t limit the type of superencipherment to those methods only. After all, anybody can choose to encipher the code blocks however they please.

Now I want to show you two of the codes from this era in a little more detail. Not so much because they were better cryptographic tools but because of their historical significance. The first is the route cipher which was used during the American Civil War. The other is an Italian code which wasn’t very popular but had an important role during the Dreyfus Affair in France.

The route cipher

In the previous post, I showed you how the Confederates used the Vigenère cipher during the American Civil War. I mentioned that one of the popular cryptographic methods the Union forces used was the so-called route cipher. And here I’m going to show you its details.

First, don’t let the name confuse you — this was more a code than a cipher.

What the route cipher means today

Actually, never mind, the name is a little confusing.

The term route cipher today refers to something different than the one used during the Civil War. It describes a transposition cipher which is a generalization of the column cipher I showed you in part 2 of the series. You still put the plaintext in a matrix with different number of columns but the ciphertext isn’t necessarily created by joining the columns. Instead, you can trace any path in the matrix you want.

For example, take the plaintext “we are surrounded”. Let’s say the key specifies a 3-column matrix:

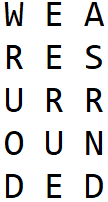
And let’s say the key also specifies the path “start from the bottom left corner and zigzag through the rows:

The ciphertext in this case becomes “DEDNUOURRSERWEA”.

Well, what I just described is obviously not a code but a standard transposition cipher. However, like I said, the route cipher used by the Union was something different.

Stager’s route cipher

The route cipher (or code) used during the Civil War was invented by Anson Stager, the co-founder of the communications company Western Union (founded in 1851, 10 years before the Civil War). Stager was also head of the Military Telegraph Department during the war.

This cipher was similar in spirit to today’s route cipher. The idea was still to put the plaintext in a matrix with different columns and read it out based on a particular pattern. However, instead of operating at the level of letters, it operated at the level of words.

I want to explain how this code works with an actual example where it was used.

Do you remember the 50-day Siege of Vicksburg from May-July of 1863? At the time there were some newspaper correspondents covering this campaign (as well as other campaigns throughout the war). Apparently, two New-York Tribune correspondents by the names Richardson and Brown were detained by Union forces under some suspicion. When president Lincoln heard about this, he was eager to correct the misunderstanding and sent a short telegram to Col. William Ludlow (source):

Notice the [Cipher.] specification above the telegram. It indicated to the telegraph operators that the telegram should be sent in cipher. The operator also appended the time of the dispatch as 4:30 PM to get the final form of the plaintext:

For Colonel Ludlow. Richardson and Brown, correspondents of the Tribune, captured at Vicksburg, are detained at Richmond. Please ascertain why they are detained and get them off if you can. The President. 4:30 p.m.

Next, the operator encoded this message with Stager’s route cipher using a specific keyword. Let me show you the details of the encoding process.

Details of Stager’s route cipher

The keys were stored in a codebook and each key indicated two things:

1. The number of columns of the matrix
2. The path of reading out the text

The path wasn’t just any path. The pattern always consisted of going up or down the columns in some order. For this message they used the key GUARD. In the codebook, this keyword specified a 5-column matrix, so the first step is to get the text in that form:

Notice that the remaining empty cells are filled with random words. The telegraph operators were free to choose those themselves.

The next step was to replace some words with important meaning with codewords from the same codebook (it contained a little over 1500 entries). The words of this message with an entry were:

• CAPTURED = WAYLAND
• THE PRESIDENT = ADAM
• COLONEL = VENUS
• RICHMOND = NEPTUNE
• 4:30 P.M. = NELLY
• VICKSBURG = ODOR

Then the matrix becomes:

Finally, the operator creates the ciphertext based on the path specified by the same keyword. In this case it is:

• up column 1
• down column 2
• up column 5
• down column 4
• up column 3

Also, at the end of each column, the operator was supposed to insert a random filler word (again, by his own choice):

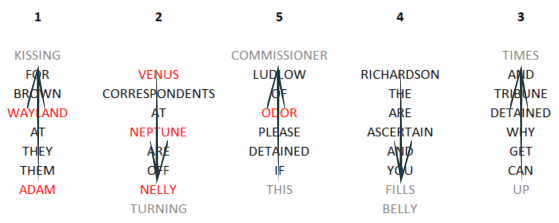
Finally, at the beginning of the message, the operator inserted the keyword itself, to indicate how to decode the text. The final ciphertext becomes:

GUARD ADAM THEM THEY AT WAYLAND BROWN FOR KISSING VENUS CORRESPONDENTS AT NEPTUNE ARE OFF NELLY TURNING UP CAN GET WHY DETAINED TRIBUNE AND TIMES RICHARDSON THE ARE ASCERTAIN AND YOU FILLS BELLY THIS IF DETAINED PLEASE ODOR OF LUDLOW COMMISSIONER

During the war, the codebook evolved to include more codewords and different paths, but the procedure remained essentially the same.

Baravelli’s code

One of the 19th century codebooks inspired by Francis Smith’s first codebook was the 1873 Corrispondenza in cifra by the Italian author Paolo Baravelli.

The codebook part was divided into 4 sections:

1. A single page with the numbers 0-9 representing vowels and punctuation marks
2. Another page with the numbers 00-99 representing consonants, grammatical forms, and auxiliary verbs
3. Ten pages were dedicated to 2-, 3-, and 4-letter syllables. Each page had 100 syllables numbered 00-99. The pages themselves were numbered with 0-9. So, to encode a specific syllable, users need to specify both the page number and the syllable number. For example, the syllable 43 on page 7 is encoded as 743.
4. One hundred pages (numbered 00-99) of dictionary words, each page having 100 words (again numbered 00-99). To encode a word, users need to specify the page number and the word number on the page (for example, 1406 for page 14, word 06).

Here’s what the first two sections looked like (source):

And here’s a sample page from sections III and IV:

In practice, the pages were renumbered between correspondents, in order to keep the code secret between them. As you can see, the first two sections also have blank spaces for manually rearranging the first digits. These procedures are a type of superencipherment.

Let me show you an example message encoded with Baravelli’s code. It was sent in a telegram by the Italian military attaché in Paris Alessandro Panizzardi on 2 November 1894:

Panizzardi’s telegram

Commando Stato Maggiore
Roma
913 44 7836 527 3 88 706 6458 71 18 0288 5715 3716 7567 7943 2107 0018 7606 4891 6165
Panizzardi

The first digit group (913) isn’t part of the message and simply indicates the telegram number. The remaining digit groups translate to:

se capitano dr e y fus non ha avuto relazione costa sarebbe conveniente incaricare ambasciatore smentire ufficialmente evitare commenti stampa

Or in proper Italian:

Se il capitano Dreyfus non ha avuto relazioni con voi, converrebbe incaricare l’ambasciatore di pubblicare una smentita ufficiale, per evitare i commenti della stampa.

Which in English translates to:

If Captain Dreyfus has not had relations with you, it would be wise to have the ambassador deny it officially, to avoid press comment.

The particular type of superencipherment Panizzardi used was the following.

The first digit of each page number and each entry in the first 2 code sections was replaced in the style of Atbash (which I showed you in a section from a previous post):

0<->9, 1<->8, 2<->7, 3<->6, 4<->5

And the second digits were replaced according to the rule:

0->1, 1->3, 2->5, 3->7, 4->9, 5->0, 6->2, 7->4, 8->6, 9->8

(Replace digits 0-4 with the first 5 odd numbers and the digits 5-9 with the first 5 even numbers.)

Finally, the two digits were exchanged. For example, according to these rules, the page number 25 becomes 07, the code for the vowel e (which in section I is 1) becomes 3, and the code for the consonant y (which in section II is 98) becomes 88.

The significance of this message is related to the infamous Dreyfus Affair.

The Dreyfus Affair

The Dreyfus Affair was a political scandal in France. It all started on October 15 1894 when Captain Alfred Dreyfus of the French general staff was arrested after being accused of high treason. The French military suspected him of having leaked secret military information about new French weapons to Germany.

Capt. Dreyfus was Jewish and, two weeks after his arrest, the antisemitic newspaper La Libre Parole published an article titled “High Treason! Arrest of the Jewish Officer, A.Dreyfus!”. This is when the story became national scandal which divided the French public for more than a decade.

The accusation was a huge deal. At the time, there was a big rivalry between France and Germany. Fifteen years earlier, France had lost a war against the North German Confederation led by Prussia. The Prussian victory created modern Germany and France lost big chunks of the regions Alsace and Lorraine. This created a lot of bitterness which was a contributing factor for World War I 50 years later.

Anyway, after an almost non-existent due process, in December Dreyfus was sentenced to life in prison in Devil’s Island where he spent the next 5 years. In 1899 he was returned to France and, after a second trial, his sentence was changed to 10 years of hard labor. However, shortly after, Dreyfus received a pardon from the French president Émile Loubet and was officially exonerated in 1906. He was even reinstated as a major and served during World War I.

You see, Dreyfus really was innocent. The leak did occur but he had nothing to do with it. But because of bias and incoherent analysis of the evidence, he spent 5 years of his life in prison for nothing.

Dreyfus’ initial conviction and the role of Panizzardi’s telegram

In September 1894, a French spy in the German Embassy in Paris gave a torn-up note to the French Military Intelligence Service. It contained the leaked information in question and triggered and immediate investigation. This note eventually became known as the bordereau.

In the eyes of many high-ranking officers, Dreyfus became the primary suspect mostly because of his Jewish origin and because he was born in the Alsace region (which had a large German population even before becoming German territory). They analyzed his handwriting and decided that it “resembled” that of the bordereau. At that point they were almost convinced of his guilt.

In La Libre Parole’s article from the 1st of November, the author accused Dreyfus of being paid by Germany or Italy. The next day, Panizzardi sent the telegram I showed you in the previous section to his chief in Rome. The French intercepted the telegram and immediately started working on decoding it, since its contents could directly implicate Dreyfus.

Let’s look at the message again:

913 44 7836 527 3 88 706 6458 71 18 0288 5715 3716 7567 7943 2107 0018 7606 4891 6165

One of the first things the codebreakers managed to identify was that Dreyfus’ name was part of the message. Since Baravelli’s codebook didn’t contain an entry for ‘Dreyfus’, Panizzardi had to encode it in pieces as Dr-e-y-fus. Spotting this wasn’t difficult because of the type of superencipherment which only manipulated the page numbers. Without superencipherment, Dr-e-y-fus becomes 227 1 98 306, whereas in the telegram it was encoded as 527 3 88 706.

Now that the telegram caught everyone’s attention, a lot of effort went into decoding the rest.

Decoding Panizzardi’s telegram

By the 6th of November, codebreakers managed to decode the first few words. They identified that 7836 stood for “Capitano” which was on page 13 and with the code 36. Then, they wrongly assumed 913 (the telegram number) stood for “Arrestato”, which was on page 06 and had the code 13. So, they decoded 913 44 7836 527 3 88 706 as “Arrestato il capitano Dreyfus…” or “Captain Dreyfus has been arrested…”. Even before breaking the rest of the message, a lot of people jumped to the conclusion that this already implicates Dreyfus.

The message was fully decoded in the middle of November. Take a look at a photo of the original telegram with the meaning of each code block added during the second trial in 1899:

As you can see, the real telegram in no way implicates Dreyfus. And you would think that it would have made the French military reconsider their initial conclusions. Unfortunately, partly because of prejudice and partly to save face, they didn’t do that. In fact, later they even forged the telegram and changed its text to:

Captain Dreyfus arrested; the Minister of War has proofs of his relations with Germany. Parties informed in the greatest secrecy. My emissary is warned.

Not only that, in 1896 they discovered the real spy was a major by the name Ferdinand Esterhazy. But in 1898, a year before Dreyfus’ second trial, they quietly acquitted Esterhazy.

Resolution of the case

During the second trial, because of the overwhelming evidence, it became clear that Dreyfus was innocent. They found him guilty anyway and sentenced him to 10 yeas of hard labor. But the tensions due to this injustice were rapidly growing and shortly after the conviction, Dreyfus was given the choice to accept his guilt and receive a presidential pardon. Which he willingly did, not wanting to spend another day in prison.

The fact that he plead guilty saved the military the trouble of explaining why they had imprisoned an innocent person for 5 years. But his pardon was enough to somewhat calm the tensions in the country. And it allowed him to seek his true acquittal.

In 1906 Dreyfus was officially found not guilty by an irrevocable judgement of the French Supreme Court. He was reinstated in the army with the rank of major. He died at the age of 75 and even participated in the First World War.

Combinatoric analysis of cryptographic codes

Cryptographic codes can be quite diverse and can have different implementations. What they all have in common is that they rely on creating sets of secret symbols to represent pieces of meaningful information. Every particular code will have its own analysis.

Following Shannon’s Maxim, we’ll assume a potential codebreaker knows which system was used to encode a message, as well as its implementation details. For example, if a message has been encoded with Baravelli’s code, we’ll assume codebreakers have a copy of Baravelli’s commercial codebook and they know what type of superencipherment is applied on the plain code (placode). On the other hand, if a message has been encoded with a type of nomenclator, codebreakers will know that the cipher part is monoalphabetic (with homophones), there are nulls, and so on.

Before I analyze each code, I’m first going to explain a general pattern for analyzing the vocabulary part of any codebook.

Analyzing vocabularies

Suppose we’re dealing with a cryptographic system that only replaces English words with digit groups, like 1033 or 13924. There’s no substitution for individual letters, letter combinations, full phrases, etc. Also, the system doesn’t use superencipherment and relies on the secrecy of the codebook itself. In other words, it uses private codebooks, not commercial ones like Smith’s or Baravelli’s. Let’s call this system Code X.

Also suppose that codebreaker Eve just intercepted a 2-word message encoded with Code X:

77777 44444

To read it, Eve needs to know what word each digit group represents. Since the codebook is secret, Eve has no idea how many words it has. All she knows is that they’re in English. English has hundreds of thousands of words, but some of them are archaic or rarely used, others are different forms of the same word, and so on. For the sake of argument, let’s assume the number is 100 000. As you’ll see, the exact number isn’t too important for our analysis.

Counting codebooks with partial permutations

In the context of a specific message, to break Code X essentially means recreating part of its codebook. Namely, the subset containing the entries associated with the words in the message. Eve can even ignore the rest and view this subset as the entire codebook. In this context, a brute-force attack means individually trying every possible code-meaning association (every possible codebook).

When you’re dealing with any combinatorics problem, always first try to create a simpler version of it. This will help you spot the general pattern or formula which you can later apply to the original (more complicated) problem.

Suppose for a moment that, instead of 100 000, English only had 2 words:

1. Morning
2. Good

How many possible codebooks can we create here? Well, only 2:

• Codebook 1
  • 44444 – Morning
  • 77777 – Good
• Codebook 2
  • 44444 – Good
  • 77777 – Morning

Now let’s include a third word to the language: “Hello”. How many possible codebooks are there this time? Well, now there are six:

• Codebook 1
  • 44444 – Morning
  • 77777 – Good
• Codebook 2
  • 44444 – Good
  • 77777 – Morning
• Codebook 3
  • 44444 – Morning
  • 77777 – Hello
• Codebook 4
  • 44444 – Hello
  • 77777 – Morning
• Codebook 5
  • 44444 – Good
  • 77777 – Hello
• Codebook 6
  • 44444 – Hello
  • 77777 – Good

Now let’s try to extract a general formula for any number of words in the language and any number of unique digit groups in a message.

The general case

Notice that we’re essentially counting the number of ways in which we can order 3 words into 2 slots. For each case, the first slot can be occupied by any of the 3 words and the second slot can be occupied by the remaining 2 words. Then, a straightforward application of the rule of product shows that there are ways to order 3 words into 2 slots.

In the general case, if we say that the number of words in English is W and the number of unique codewords (digit groups) in the message is c, the total possible codebooks is essentially the number of partial permutations of W words into c slots:

   

To get more intuition about partial permutations, take a look at the permutations section of my introductory post to combinatorics.

As an exercise, try to calculate the number of codebooks if you assume the vocabulary also contains 2- or 3-word long expressions. The solution here isn’t necessarily unique and will depend on the types of simplifying assumptions you make. If you decide to give it a try, feel free to share your solutions in the comment section below.

Alberti’s code

Alberti’s code has 336 symbols in total. These symbols are 2-, 3-, or 4-digit groups and each can represent an arbitrary word, phrase, or a full sentence. Now, I’m going to assume that we’re only dealing with words and maybe phrases, since sentences can be of arbitrary length and complexity and there’s no way to really count them. But, as you’ll see, the situation is “bad” enough even with just words.

The entire codebook consists of 336 entries, so there’s 336 slots for words. The formula for the number of possible codebooks here (not counting phrases) is:

   

If we assume W is 100 000, the total number of possible codebooks is:

   

I can’t even begin to tell you how large a number this is. If you include phrases too, it becomes much worse. Don’t ever even think about trying to brute-force your way out of a problem like that!

If you remember, I also told you that Alberti recommended using his polyalphabetic substitution method to superencipher the digits. But in the previous post I told you that his method involved sending the keys along with the ciphertext, which is a violation of Shannon’s Maxim. So we can’t really rely on the secrecy of the “key” and there’s no point in trying to analyze this part. However, even without superencipherment, breaking this with brute-force is practically impossible.

Of course, the problem with this system is that you can only hide the meaning of 336 words or phrases, which doesn’t leave you much room for writing arbitrary messages. But that’s not a problem with its security per se, so I’m giving this code the maximum score.

Brute-force security score: 10

Mary’s nomenclator

The vocabulary part of Mary’s nomenclator (or any other nomenclator) has the same general analysis. Namely:

   

Where W is the number of words in the language and C is the number of symbols in the codebook. From this feature alone I could give Mary’s code a score of 10. Which I will. But if I left the analysis here, it would be rather boring, wouldn’t it?

So, let’s assume for a moment that Mary’s nomenclator didn’t have a vocabulary part but only nulls and homophonic substitution. This analysis will also apply to other nomenclators.

Let’s say the nomenclator has a total of S symbols that can stand for letters or nulls and the plaintext alphabet is A letters long. Of these S symbols, N are nulls and each letter in the alphabet has H homophonic substitutes. Furthermore, let’s assume code symbols only substitute single letters and not letter combinations.

This means that the total number of symbols in the codebook is:

   

We can safely assume Eve knows the values of A and S. Then, notice that if Eve knows the value of N, she can easily calculate the value of H, and vice versa.

So now the question is: in how many ways can the S symbols be distributed across all letters and nulls?

Counting symbol distributions across nulls and homophones

Let’s try to simplify this problem too by assuming the alphabet only consists of the letters ‘a’ and ‘b’. That is, A = 2. Let’s say each letter has 3 homophones (H = 3) and there are 2 nulls (N = 2). This means that the code has a total of 8 symbols:

   

For simplicity, let’s assume these symbols are the digits 1-8. To reconstruct the associations used by a particular nomenclator, Eve needs to fill the table below with the right values:

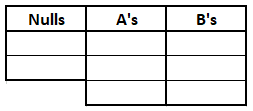
For example, one possibility is:

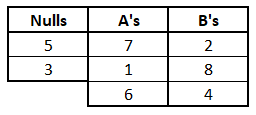
There’s 8 symbols and 8 slots, so there’s 8! ways to distribute the 8 numbers across the slots. But notice that the order of the numbers in each column doesn’t actually matter. For example, the following table represents an identical association rule as the one above:

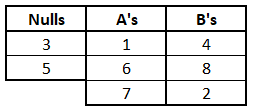
So Eve doesn’t really have to try all 8! possibilities but only the ones where the symbols under each column are different (regardless of their order in the column). Therefore, she needs to divide the value 8! by the number of permutations of each column:

   

This is nothing but an application of the multinomial coefficient I introduced in my post on combinatorics.

More generally, for any S, A, N, and H, the number of possible associations is equal to:

   

Or with a more compact notation:

   

Here through are the number of homophones for each letter. And the notation is analogous to the sum operator but for multiplication instead of addition.

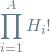
Final evaluation of Mary’s code

Because we assumed the number of homophones (H) is the same for each letter, we can use an even more compact notation:

   

In the code we’re analyzing, Mary used an alphabet of 23 letters and each letter had 4 homophonic substitutes. Also, she had 31 null symbols. From the values A=23, H=4, and N=31, we get:

   

And the number of possible associations becomes:

   

This is also a number that will discourage any brute-force attempts. On top of that, when you add the symbols for letter combinations and full words, breaking her code (or any other nomenclator, for that matter) through sheer brute-force is practically impossible.

For example, if we include the 182 symbols for full words, we will need to add 182 to the already existing 123 symbols, as well as the term 182! to the denominator. And we also need to add the expression . If we assume W = 100 000, the final number becomes:

   

Absolutely impossible to break!

As an exercise, you can try to do the same calculations after including letter combinations in the list of symbol associations (or by assuming lack of knowledge of N and H).

Brute-force security score: 10

Stager’s route cipher

When it comes to the transposition part, the route cipher today and Stager’s version have very similar combinatoric analysis. Since in principle any path is possible, all permutations are valid candidates for the true order. In today’s version of the cipher, we’re considering the permutations of individual letters, whereas with Slater’s cipher we’re considering the permutations of the words. So, in one case the number of possible keys is l! and in the other it’s w!, where l/w are the number of letters/words in the message.

The word substitution part has the same analysis as Alberti’s code. Namely, , where c is the number of codewords in the message and W is the number of words in the language.

Therefore, the total number of possible composite keys (word permutations + word substitutions) is:

   

The first term alone creates a huge number. Combined with the transposition, brute-force attacks are practically impossible for this system too.

Brute-force security score: 10

Baravelli’s code

Baravelli’s code’s secrecy depends entirely on superencipherment. This is true for any other commercial codebook (like Smith’s or Slater’s), since anybody can purchase a copy and have access to the entries. By Shannon’s Maxim, users can’t assume that eavesdroppers won’t figure out which commercial codebook is used.

Let’s analyze the security of the superencipherment procedure with which Italians used the code during the Dreyfus Affair. Remember, the codebook in Baravelli’s code consists of 4 sections of 10, 100, 1000, and 10000 entries, respectively. And each entry is a number between 0 and 9/99/999/9999 (depending on the section). In their superintendence procedure, Italians simply substituted each code number with another having the same number of digits. The effect of that is essentially to randomly shuffle the entries in each section.

Therefore, the total number of possible codebooks here is simply equal to the sum of the permutations of each section:

   

The numbers we’re working with are becoming more and more impressive, aren’t they?

Brute-force security score: 10

Summary

That was a lot of information. If you managed to stick to the end, congratulations! I’m assuming this means you found the post interesting which always makes me happy.

In today’s post I showed you the evolution of cryptographic codes throughout the centuries. The first code I introduced you to was Alberti’s code from the 15th century. It’s based on Alberti’s disk which I showed in the previous part of this series.

Apart from Alberti’s code, the real birth of modern cryptographic codes came from the nomenclator. It was invented and used between the 14th and 18th centuries and was a mix between a codebook and a monoalphabetic substitution cipher. The other new concepts I talked about in relation to the nomenclator are nulls, homophones, and polyphones.

In the 19th century, communication technologies themselves underwent a revolution (most notably, after the invention and commercialization of the telegraph). This is when nomenclators were replaced by proper codebooks with tens of thousands of entries. I showed you example pages from the commercial codebooks of Smith, Slater, and Baravelli. I also showed you Stager’s route cipher which is rather different in nature and is also using a combination of a codebook and a cipher. The new concepts from this period were superencipherment, placode, and encicode.

I also talked about some important historical events in which some of these codes were used. Namely, the Babington Plot, the American Civil War, and the Dreyfus Affair.

Brute-force security scores

You probably noticed that all codes I showed you here had a maximum security score of 10. Most ciphers I showed you in the previous parts had a score less than 10. After all, this is to be expected, isn’t it? As cryptography advances, breaking cryptographic systems with pure brute-force approaches naturally becomes much more difficult or outright impossible.

Having said that, just because a cryptographic system is secure against brute-force attacks, doesn’t mean it’s secure against more sophisticated codebreaking algorithms. In fact, every single code or cipher I’ve shown you so far could be and was broken.

Anyway, let me give a summary of the cryptographic security of the codes from this post. First, here’s what each term in the formulas below stands for:

• W: the (approximate) number of words in the language
• C: the number of word entries in the codebook
• S: the number of symbols in a codebook
• H: the number of homophonic substitutions per letter
• N: the number of nulls
• A: the number of letters in the alphabet
• w: the number of words in a message
• c: the number of codewords in a message

For nomenclators, we have the constraint:

   

And here are the final evaluations:

• Alberti’s code
  • Number of keys formula: 
  • Brute-force security score: 10
• Mary’s nomenclator
  • Number of keys formula: 
  • Brute-force security score: 10
• Stager’s route cipher
  • Number of keys formula: 
  • Brute-force security score: 10
• Baravelli’s code
  • Number of keys formula: 
  • Brute-force security score: 10

---

Want to see how codes (and ciphers) continued to evolve in the 20th century? Here’s part 5 of my series, dedicated to World War I cryptography.