
“Simple explanations are better than complex explanations.” — have you heard this statement before? It’s the most simplified version of the principle called Occam’s razor. More specifically, the principle says:
A simple theory is always preferable to a complex theory, if the complex theory doesn’t offer a better explanation.
Does it make sense? If it’s not immediately convincing, that’s okay. There have been debates around Occam’s razor’s validity and applicability for a very long time.
In this post, I’m going to give an intuitive introduction to the principle and its justification. I’m going to show that, despite historical debates, there is a sense in which Occam’s razor is always valid. In fact, I’m going to try to convince you this principle is so true that it doesn’t even need to be stated on its own.
In order to be able to follow the second (and main) part of this post, you need to have basic familiarity with Bayes’ theorem, combinatorics, and compound probability. Reading this post, this post, and this post should get you covered.
Table of Contents
Introduction to Occam’s razor

Occam’s razor is one of the oldest principles in philosophy of science. Even though it’s named after the 14th century English philosopher William of Ockham, its roots are traceable to even earlier periods.
Prominent philosophers and scientists who have proposed variants of the principle include Ptolemy, Aristotle, Aquinas, Kant, Newton, Einstein, and many others.
So what is Occam’s razor? Let me introduce it with a concrete example.
Occam’s razor example
Say you’re reading a legal case on an attempted carjacking of a luxury car. The first excerpt you come across is the following:
Prosecutor: “You were caught sitting inside that car after breaking one of the side windows.”
Defendant: “I wasn’t stealing anything. I was just trying to hide from the rain.”
Here we have the observation that the defendant was found inside a car that didn’t belong to them. The first and main explanation is that they were there to steal the car. Let’s call this Explanation A. However, the defendant offers an alternative explanation. It’s not that they had any intentions to steal, they were just trying to hide from the rain. Let’s call this Explanation B.
You probably immediately dismiss the latter, but why? So far you haven’t heard any evidence in favor of either explanation. Why aren’t they equally likely to be true?
One reason could be that you’ve never heard of a person breaking inside a car to hide from the rain. On the other hand, breaking into a car to steal it is much more common and makes A more likely to be true. But that’s not the only problem. Unlike A, with B there’s also a strong sense of incompleteness.
You continue reading:
Prosecutor: “This is very unusual. Why would you break into a car to hide from the rain?”
Defendant: “The car was the closest thing around. It was my only chance to hide.”
Prosecutor: “Why didn’t you look for a more appropriate place to hide, even risking getting a little wet?”
Defendant: “I have a rare skin condition that makes me very sensitive to water. I shouldn’t stay under rain for longer than a minute.”
Breaking it down
As you continue reading, Explanation B seems to answer more questions, but for some reason it doesn’t get much more believable. Why is that?
Notice how with each extra piece of information the defendant makes Explanation B more complete at the expense of also making it more complex. And while Explanation A is already (almost) complete, B needs a lot of additional statements and clarifications.
Each of these statements is an extra hypothesis that needs to be independently verified. In science, such hypotheses are referred to as ad hoc. Generally speaking, ad hoc hypotheses increase the explanatory power of a theory while also increasing its complexity and reducing its predictive power.
Bottom line is, getting the explanatory power of B to the level of A makes B much more complex than A. Hence, according to Occam’s razor, A is preferable to B:
A simple theory is always preferable to a complex theory, if the complex theory doesn’t offer a better explanation.
Traditional justifications for Occam’s razor
Is Occam’s razor valid? So far, I’ve only appealed to your intuition, but there are more rigorous ways to answer this question.
Traditionally, philosophers and scientists have attempted to justify the principle with a combination of rational and empirical arguments.
Rational justifications
Consider this quote from the philosopher Elliott Sober:
Just as the question ‘why be rational?’ may have no non-circular answer, the same may be true of the question ‘why should simplicity be considered in evaluating the plausibility of hypotheses?’
This is an example of a rational (a priori) justification for the principle. The argument here is that we need a principle like Occam’s razor to choose between rival theories or hypotheses when there isn’t a better way to do so (such as when they explain the observations equally well).
This may not be the most convincing argument, but it has some practical value. After all, even if simplicity by itself doesn’t make a theory “more true”, there are other benefits of working with simple theories. For one thing, they tend to be easier to understand and often have a higher aesthetic appeal.
Empirical justifications
Empirical arguments for the principle focus on instances of its real-world success. If Occam’s razor is a valid principle, all else being equal, theories that were once simpler must frequently “beat” their rivals when more evidence becomes available. Let’s look at a concrete example.
The 18th century naturalist Georges-Louis Leclerc, Comte de Buffon proposed a law currently known as Buffon’s Law. Roughly, it says that geographical regions separated by natural barriers (like mountains and oceans) have distinct biological species, with occasional exceptions.

According to Charles Darwin, the law was explained by the natural dispersal of species at separate geographical regions over time. Being separated from each other, they also evolved independently. The occasional exceptions were explained by anomalous dispersal (also known as “jump dispersal”) in the recent past. This was caused by rare factors like ocean currents, wind, floating ice, and (more recently) human activities which allowed species from separate regions to mix in common environments.
Opposed to this explanation, the botanist Léon Croizat suggested that historical tectonic changes (rather than dispersal), such as newly-formed mountains, were responsible for Buffon’s Law. He explained exceptions with historical land bridges between regions (that stopped existing at a later point in time).
Croizat’s hypothesis postulates the existence of entities that are no longer observable (the land bridges). For this reason, biologists have criticized it for introducing unnecessary complexity in its explanation of the law. Hence, support for Darwin’s hypothesis would be an empirical “point” in favor of Occam’s razor. In fact, Darwin’s theory has received strong support, including in some recent findings.
Of course, available evidence neither proves nor rejects either hypothesis. And even if it did, that by itself would only be weak evidence in favor or against Occam’s razor.
Other justifications
To most people, Occam’s razor makes intuitive sense, but academics have tried to find more robust justifications for it. Why use simplicity as a deciding factor in theory selection?
I already gave examples of rational and empirical arguments in favor of the principle. Of course, other arguments exist, including aesthetics and elegance considerations, which have also been occasionally used as justifications.
However, in the following section I want to introduce a third type of justification. It is relatively new and comes from probability theory. In some sense, it’s a combination of a rational and an empirical justification. And in another sense, it’s the main focus of this post, so let’s dive in.
Probabilistic justification for Occam’s razor
Let’s go back to the original question. Why is it a good thing for a hypothesis/theory to be simple? Well, if simpler theories generally tend to be closer to the truth, then simplicity is good because it brings us closer to the truth. This is the essence of the empirical arguments for Occam’s razor.
But simply counting “simple” and “less simple” theories and what percentage of them turn out to be true isn’t a very rigorous or reliable approach.
The main problem is that none of the crucial concepts is well defined. What exactly does it mean for a theory to be simple? How can we compare two theories in terms of simplicity?
Also, what does it mean for a theory to “turn out to be true”? There are hardly any proofs of certainty in science, so it’s never safe to say that any theory is 100% true or false. A third problem is comparing theories in terms of how well they explain the available observations. What exactly does it mean for a theory to explain something better than another theory?
This all seems too vague and subjective.
A better approach is to adopt a formal definition of simplicity which, at least partly, coincides with a more intuitive one. Then we also need a formal approach to establishing the truth value of theories. Finally, we need to formalize what it means for a theory to explain an observation. If we can then show that, by only manipulating the simplicity of a theory we can increase its truth value, this would be a much better justification for Occam’s razor.
Formalizing “truth”, “simplicity”, and “degree of explanation”
One of the main reasons why absolute truth can never be established for almost any real world problem is underdetermination. In short, any observation is consistent with an infinite number of potential explanations (theories). Therefore, no amount of evidence can ever prove a theory with complete certainty. That said, not all explanations are equally plausible.
In my post discussing the nature of probabilities, I showed how they can be viewed as degrees of belief or degrees of uncertainty. This means that they’re a great candidate for ranking theories according to their truth values. Let’s define the truth of a theory as its probability. If P(Theory) = 1, then the theory is certainly true. If P(Theory) = 0, it’s certainly false. And any number between 0 and 1 means there’s uncertainty about its truth.
So far, so good. Next, we need to define simplicity. A natural way is to relate it to the number of independent assumptions underlying the theory. Fewer assumptions = simpler theory. Makes sense?
Almost. We also need to consider the simplicity of the assumptions themselves. I’m going to come back to this point in the next section. For now, let’s just say a theory is simple if it has few assumptions that are themselves simple.
Finally, we need to say what it means for a theory to explain an observation. In the most basic sense, if any part of the observation is inconsistent with what the theory had predicted prior to the observation, we count that part as not explained. So, the degree to which a theory explains an observation is the degree to which the observation is consistent with the theory’s predictions.
This may sound too abstract, but I promise it’s all going to become much clearer in the following sections.
Applying the new definitions
Let’s start with a hypothetical theory, called Theory A. Let’s also call all observations relevant to the theory Observations B (experiments, surveys, correlation data, and so on). Then, the degree to which A is consistent with B is the conditional probability P(Observations B | Theory A), also called the likelihood. The probability that the theory is true is the conditional probability P(Theory A | Observations B), also known as the posterior probability. From now on, I’m going to refer to these two simply as P(B|A) and P(A|B).
Naturally, we can relate them using Bayes’ theorem:
Imagine an alternative theory, called Theory A’, which tries to explain the same observations B. Its posterior probability is:
Here’s the crucial expectation. According to Occam’s razor, if A and A’ explain B equally well, the simpler of the two will have a higher posterior probability. Let’s see if that’s true.
Notice that the evidence term P(B) doesn’t play a role in this comparison, since its value doesn’t depend on the theory. Then, the comparison depends solely on the products P(B|A) * P(A) and P(B|A’) * P(A’).
Let’s simplify this even further by assuming the prior probabilities P(A) and P(A’) are equal. This reduces the comparison to the likelihood terms P(B|A) and P(B|A’). Since Occam’s razor is supposed to be universally valid, it must also be valid in this special case.
Now, if we manage to show that, given the same explanatory power, simpler theories always yield higher likelihood values, we will essentially prove the validity of Occam’s razor!
In the next sections I’m going to do just that by demonstrating it with an example, followed by the formal intuition for why it works in the general case.
A detailed example for illustrating the validity of Occam’s razor
Imagine a cardboard with a 10 by 10 grid lying on a table.
You also see 15 black beans of equal size randomly dispersed next to it. Each of the 100 squares of the board is large enough to fit exactly one bean.
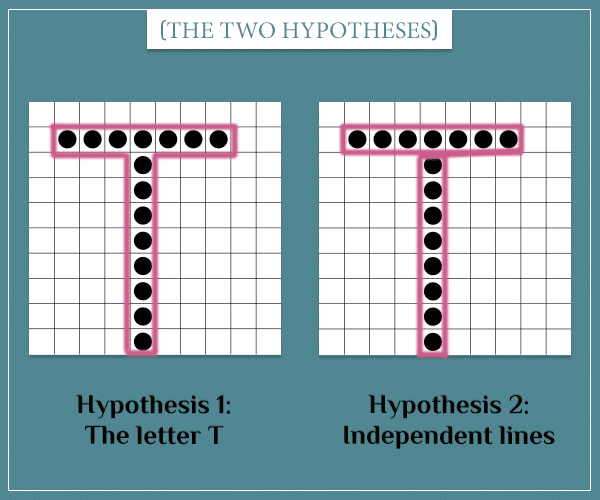
You leave the room and see another person enter after you. In about 10 minutes you come back and find that the other person has ordered the beans on the board, forming the following pattern:
The person who entered the room after you has left, so you can’t ask them why they did it. However, this looks just like the English letter T, so you suspect this is what they were trying to do (maybe it’s the first letter of their name?). Let’s call this Hypothesis 1.
But of course, that’s not the only possible explanation. They could have also wanted to form a horizontal and a vertical line with those exact lengths. In that case, the T-like pattern would be a mere coincidence (Hypothesis 2).
Yet a third hypothesis is that the person placed the beans without following any rule. In other words, they chose the 15 squares completely randomly. Let’s call this Hypothesis 3.
Let’s also call the “T” pattern itself Pattern T.
I deliberately selected the hypotheses with an increasing level of complexity. H2 is a more complex explanation of T because it explains the positions of the horizontal and vertical lines separately (in H1 they are bound together). H3 is even more complex because it explains the position of each bean separately!
Following the discussion above, we need to demonstrate the truth of the following inequality of the likelihood terms:
Let’s do that.
By the way, reading my post introducing combinatorics will help you a lot in being able to follow the calculations.
Calculating P(T | H1)
Think about what this probability represents. Here’s a more verbose reading of P(T | H1):
- The probability that the person would form the observed pattern, given that they intended to form the letter T.
If you go back to the figures, you’ll see that there are only 8 possible ways to form the letter T. This is because there are 2 possible vertical positions and 4 possible horizontal positions (2 * 4 = 8). Therefore:
Calculating P(T | H2)
Since in this case the two lines are not attached to each other, there are new possible combinations.
I’m deliberately going to go a little fast over the calculations, since the details aren’t that important. If you have any questions, feel free to leave them in the comment section.
Let’s start with the vertical line. There are 3 possible vertical positions and 10 possible horizontal positions. So, overall there are 3 * 10 = 30 possible positions.
For each of the 30 positions of the vertical line, there are 2 vertical and 4 horizontal possible positions for the horizontal line: 2 * 4 = 8 (above and below it). This means that the total number of possible configurations is 30 * 8 = 240.
But we’re not done just yet. Notice that if the vertical line is close enough to one of the sides, there’s enough room for the horizontal line to squeeze to its left or to its right. This gives 3 * 8 = 24 additional possibilities for the horizontal line. The 8 comes from the 8 additional vertical positions for the horizontal line and 3 is the number of possible horizontal positions next to the vertical line.
There are 2 horizontal and 3 vertical possible positions for the vertical line where it touches one of the sides. Therefore, we get 2 * 3 * 24 = 144 additional combinations. Careful with counting the same combinations more than once!
The calculations for when the vertical line is 1 or 2 squares away from each side are very similar. They yield 96 and 48 additional combinations, respectively. Therefore, the final number of combinations is:
Finally we can calculate P(T | H2) as:
Calculating P(T | H3)
Remember that, according to H3, the position of each bean was determined independently of the others. There are 100 squares and 15 beans. In how many possible ways can the beans be placed on the board?
You can calculate this quite easily using the binomial coefficient:
In our case, N = 100 and K = 15, which gives a total of 253338471349988640 combinations. Whoa!
So, the final likelihood is:
Analyzing the example
Notice that all 3 hypotheses explain the observation perfectly. Yet, look at the gigantic difference between their likelihoods! Even under the equal prior probability assumption, H1 is 66 times more probable than H2 and 31 667 308 918 748 580 times more probable than H3! You can verify this is true by calculating the ratios P(T | H1) / P(T | H2) and P(T | H1) / P(T | H3).
Of course, you could argue that their prior probabilities shouldn’t be equal. But the point is, regardless of what the prior probabilities are, the simplicity of a hypothesis is a huge factor in determining the value of the likelihood term. And because the posterior probability is proportional to the likelihood, a hypothesis gets “probability points” merely by being simpler than its rivals.
A big win for Occam’s razor!
Formal intuition
Earlier I related simplicity of an explanation to the number and simplicity of its underlying independent assumptions. Let’s apply this criterion to the three hypotheses from the example.
What do you have to assume for H1? If you think about it, once you assume the position of the top left bean, you’re no longer free to assume anything about the positions of the remaining beans. According to H1, the pattern is always supposed to be a T and only its position is allowed to vary. Furthermore, there are only 8 allowed positions for the top left bean, as the remaining positions don’t allow for the entire T to fit inside the grid.
On the other hand, H2 doesn’t require the pattern to be a T. It only requires that the pattern contains an 8-bean-long vertical line and a 7-bean-long horizontal line. Therefore, you need to make independent assumptions about the positions of both lines.
H3 is even more complex because there you need to make independent assumptions about the positions of all 15 beans.
All hypotheses explain the pattern completely. The only difference is in their simplicity, but you saw the kind of difference that can make! The reason more independent assumptions lead to a lower probability ultimately rests on the following rule:
- The probability of a number of independent assumptions to all be true is equal to the product of their individual probabilities.
And because probabilities are numbers between 0 and 1, multiplying more of them reduces the value of the final product.
If you need a refresher on this, check my post on compound probabilities.
Summary
In the past, some philosophers saw value in Occam’s razor because they believed nature itself was simple. Hence, they expected theories explaining nature to also be simple. However, today we know that natural observations and their explanations can be very complex and messy. Therefore, we need stronger arguments to justify the virtue of simplicity in theories.
In this post, I briefly introduced you to rational and empirical justifications of Occam’s razor. But I mostly hope to have demonstrated that there’s a strong mathematical and probabilistic argument behind the principle. Namely, if you need to make too many and complex independent assumptions to explain an observation, the posterior probability of your explanation will get a natural “penalty”, regardless of how well it explains the observation. In other words, if your explanation requires too many independent (and unlikely) things to be true, it has to offer better explanations of phenomena than any rival explanations with fewer/simpler assumptions.
Of course, if a theory doesn’t properly explain an observation, its simplicity is worthless. For this reason, in the real world there’s often a trade-off between a theory’s simplicity and how well it explains a set of observations.
Earlier I mentioned the concept of ad hoc hypotheses. These are special purpose hypotheses that are typically used to save a theory from being falsified by an observation.
But you saw that you can’t really “cheat” Bayes’ theorem by introducing ad hoc hypotheses. If an ad hoc hypothesis adds little to the explanation, any boost to the posterior probability will be canceled out (or worse) by the complexity added by the hypothesis.
I started this post by promising to show you that Occam’s razor doesn’t need to be stated as a separate principle. I hope now you see why this is true — the principle (or at least a version of it) follows naturally from the laws of probability. Hence, asserting it independently is redundant and… complicates things unnecessarily.
Paradoxically, Occam’s razor renders itself obsolete!

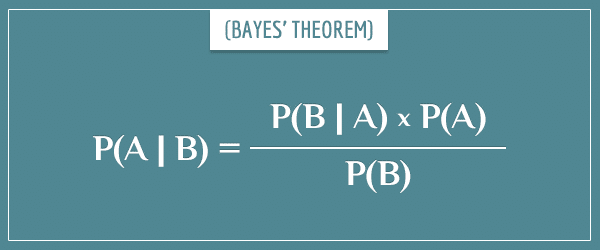
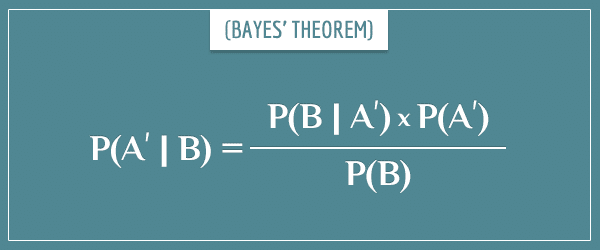


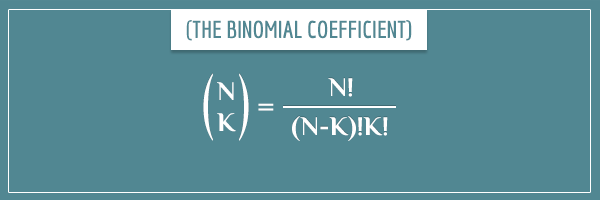
Very nice post! I just wanted to note that you are essentially describing the rationale behind ‘Bayesian Model Selection’, where the posteriors will vary based on the marginal likelihoods of the hypotheses or models. The more parameters in the models and the broader the prior distributions on them, the lower their marginal likelihoods, all else being equal.
Another route to Occam’s razor is in the priors themselves. The more independent assumptions a hypothesis makes, the lower its prior. This is a simple consequence of the multiplicative rule of probability for independent events.
In any case, you are correct that probability can pretty much explain our intuitive notion of why ‘simpler ‘theories are to be preferred.
Good observation, YF! Indeed, Bayesian model selection is what I was essentially doing in the examples above. Model selection is a more general concept that I briefly talked about in my Bayesian vs. Frequentist approaches post (I referred to it as ‘model comparison’). In fact, if you take an even broader view, it can be viewed as an epistemological concept. But you’re absolutely right that the Bayesian approach to model selection is the easiest and most natural way to show the emergence of Occam’s razor.
I have to partly disagree with your point about priors themselves being a second route to Occam’s razor. I agree that most of the time it would be a good practice to give higher priors to simpler theories, but that is more a consequence of Occam’s razor than a justification for it. In other words, if we have already (somehow) justified Occam’s razor and hence see simplicity as a good criterion for model selection, we have a strong argument for lowering the priors of models/hypotheses/theories that seem overly complicated for what they’re trying to explain, but we still need to have arrived at Occam’s razor beforehand.
Having said that, the beauty of the justification I talked about in this post is that it naturally covers the priors as well. It’s obvious you have a good background in Bayesian inference so you know that “today’s posterior is tomorrow’s prior”. So, successive and consistent application of Bayes’ theorem would lead to priors that will be updated just the right amount according to both their explanatory power and their simplicity (number/parsimony of the underlying assumptions).
Let me know what you think!
Thanks for the reply! I guess I didn’t quite understand why you brought up the conjunction rule of probability in the context of your explanation of Occam’s razor based on likelihoods. Could you please explain a bit more where that enters into the likelihood calculation?
For instance, in your post you say that “All hypotheses explain the pattern completely. The only difference is in their simplicity.” My interpretation was that you were referring to the intrinsic simplicity of the hypotheses themselves, which in turn would be reflected by their priors.
Incidentally, the following paper argues that the conjunction rule can be invoked to explain why simpler theories are to be preferred, and that this probabilistic advantage is located at the level of the priors, not the likelihood.
Brit. J. Phil. Sci. 68 (2017), 781–803
Quantitative Parsimony: Probably
for the Better
Lina Jansson* and Jonathan Tallant*
ABSTRACT
Our aim in this article is to offer a new justification for preferring theories that are more
quantitatively parsimonious than their rivals. We discuss cases where it seems clear that
those involved opted for more quantitatively parsimonious theories. We extend previous
work on quantitative parsimony by offering an independent probabilistic justification for
preferring the more quantitatively parsimonious theories in particular episodes of theory
choice. Our strategy allows us to avoid worries that other considerations, such as pragmatic
factors of computational tractability and so on, could be the driving ones in the
historical cases under consideration.
Thus, I think there are potentially two probabilistic routes to Occam’s razor: one at the level of the priors, and the other at the level of likelihoods.
Please let me know what you think..
Let’s call the particular observation we’re trying to explain O. Let’s call two rival hypotheses for explaining O H1 and H2.
Let’s also define the simplicity of a hypothesis as the number of independent parameters of each hypothesis (assuming all parameters have identical ranges). The likelihood term represents the probability of O, given H1 or H2.
Now, let’s say H2 is more complex and therefore has a higher number of free parameters. What this means is that, prior to O, it would have predicted that we would observe not only O but many alternatives to O. A simpler hypothesis would have predicted O and fewer alternatives. Let me know if this makes sense so far.
Here’s some more intuition. Because a more complex hypothesis predicts more alternatives, each of those alternatives will get a lower probability. This is because they all have to split the total probability mass of 1 (of the whole sample space). So, for example, if we only have 3 alternatives and wanted to distribute the total probability equally among them, each could get 1/3rd, but if we have 100 alternatives, each can only get 1/100th.
So, if H2 is more complex, it will predict O with a lower probability than H1 will, and hence we will get the following inequality for the likelihood terms: P(O|H1) > P(O|H2).
Notice, I didn’t assume anything about the priors P(H1) and P(H2). If defining simplicity as the number of free parameters makes intuitive sense, then Occam’s razor follows naturally without having to assume anything else. I mentioned the rule of conjunction in order to give mathematical intuition for why an observation “occupies” a smaller percentage of a complex hypothesis’ sample space than a simpler hypothesis’ (which is another way of saying ‘has a lower likelihood’). Namely, more free and independent parameters means a higher number of independent terms need to be multiplied together to form the final likelihood term. And because we’re multiplying values between 0 and 1, with each extra term the final product will get smaller.
Did I manage to answer your questions? Let me know if any part isn’t entirely clear.
Thanks, yes, that clarifies things for me.
Would you agree, however, that the conjunction rule can be used at the level of the priors to favor ‘simpler’ hypotheses in the case where the competing hypotheses don’t have free parameters?
Well, every hypothesis needs at least one free parameter in order to predict more than one alternative. But I think you can successfully apply the conjunction rule at the level of the priors, it’s more a matter of perspective. Like I said in one of the earlier replies, a hypothesis’ prior is supposed to reflect how much support it has received from all available evidence. If the hypothesis is simple, all else being equal, it will naturally have received “probability points” by successively applying Bayes’ theorem for each piece of evidence.
When it’s not possible to construct an informative prior formally, one can use this line of reasoning to implicitly assign a higher prior to a simpler hypothesis. You can also use the rule of conjunction at the level of priors, in cases where you have a “compound hypothesis” (like in the case of the paper you linked to earlier). But then you would still be implicitly using it at the level of the likelihoods as well, as each of the sub-hypotheses that form the compound hypothesis will have a prior that reflects its past updates from available evidence (through Bayes’ theorem, where the likelihood term naturally yields Occam’s razor).
Thanks for the helpful reply and for taking the time to consider my comments. Looking forward to more great posts!